• Если   и  , то  ;

• Если   и  , то аналогично  .

• Правило Лопиталя можно также применять к неопределенностям типа 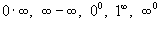 . Первые две неопределенности   можно свести к типу   или   с помощью алгебраических преобразований. А неопределенности 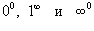  сводятся к типу 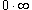  с помощью соотношения

• 

• Правило Лопиталя справедливо также и для односторонних пределов. 

• Формула Тейлора показывает поведение функции в окрестности некоторой точки. Формула Тейлора функции часто используется при доказательстве теорем в дифференциальном исчислении.

• Формула Тейлора

• 

• , где R_n(x) - остаточный член формулы Тейлора.

• Остаточный член формулы Тейлора

• В форме Лагранжа:

• 

• В форме Коши:

• 

• Если после изучения данного теоретического материала (Формула Тейлора) у Вас возникли проблемы при решении задач на данную тему или появились вопросы образовательного характера, то Вы всегда можете задать их на нашем

ТАБЛИЦА ПРОИЗВОДНЫХ

1.

степенные функции

2. 

2a.

2b.

2c.

2e.

( )

показательные функции

2. 

3a.

логарифмические функции

2. 

4a.

( )

тригонометрические функции

2. 

3. 

4. 

5. 

обратные тригонометрические функции

2. 

3. 

4. 

5. 

гиперболические функции

2. 

3. 

15.

16.

показательно – степенные функции

17.

модуль функции

18. , ,

где – функция знак u

(сигнум u).

Правила дифференцирования

1. 

1a.

2. 

3. 

4. 

5. Сложная функция

6. Параметрически заданная функция

7. неявно заданная функция уравнением

чтобы найти производную неявно заданной функции, нужно продифференцировать обе части уравнения считая y функцией от х и применяя правило 5 дифференцирования сложной функции;

8. Логарифмическое дифференцирование