
- •Искусственный интеллект. Основные направления и этапы развития.
- •Структура мозга. Уровни моделирования. Основные элементы моделей.
- •Виды функций активации
- •Классификация нейронных сетей
- •Применение нейронных сетей
- •Методика решения формализуемых задач в нейросетевом базисе
- •Настройка нейронной сети на решение прикладных задач
- •Обучение нс Основные понятия
- •Основные алгоритмы обучения нс без обратных связей
- •Персептронные алгоритмы обучения Алгоритм обучения по правилу Хебба
- •Алгоритм обучения Розенблатта
- •Процедура Уидроу-Хоффа
- •Обучение многослойной нейронной сети без обратных связей Математическая постановка задачи обучения
- •Алгоритм обратного распространения ошибки
- •Генетические алгоритмы оптимизации
- •Суть генетического алгоритма
- •Методы формирования популяции
- •Иллюстрация работы генетического алгоритма
- •Особенности реализации генетических алгоритмов
- •Модификация основных параметров га
- •Мобильные га
- •Динамическое изменение параметров в процессе выполнения га
- •Разновидности га
- •Применение генетического алгоритма к обучению многослойного персептрона
- •Рекуррентные и рециркуляционные сети
- •Сеть Хопфилда
- •Применение сети Хопфилда к решению задач комбинаторной оптимизации
- •Сеть Хемминга
- •Самоорганизующиеся нейронные сети Самоорганизация в нс
- •Конкурентное обучение
- •Сеть Кохонена
- •Алгоритмы кластеризации
- •Пороговый алгоритм
- •Алгоритм максимального расстояния
- •Алгоритм внутригруппового среднего (метод k-средних, k-means clustering, c-means clustering)
- •Алгоритм нечётких k-средних (fuzzy c-means clustering)
- •Алгоритм состязания процедур соединения и разделения.
- •Сети адаптивного резонанса
- •Основы адаптивного резонанса
- •Архитектура art
- •Комбинированные нс
- •Иерархический классификатор
- •Нейронные сети с функциональными связями
- •Решающие деревья
- •Методы проектирования нейросетевых архитектур для решения прикладных задач
- •Выбор топологии нс для решения задач нейроуправления
- •Практическое применение нс Управление движением робота по заданной траектории
- •Обучение и формирование обучающей выборки для управления мобильным роботом
- •Тестирование робота
- •Автономное управление мобильным роботом
Основные алгоритмы обучения нс без обратных связей
В 1957 году американский физиолог Ф. Розенблатт предпринял попытку технически реализовать физиологическую модель восприятия, что позволило бы имитировать человеческие способности правильно относить наблюдаемый объект к тому или иному классу.
Розенблаттом была разработана модель нейронной сети, получившая название персептрон (от слова «перцепция» – восприятие).


Персептрон предназначен для работы в двух режимах: обучения и распознавания.
Для организации обучения сетей типа «персептрон» вычисляется ошибка рассогласования ej между желаемым сигналом выходного нейрона dj и реальным значением выхода нейрона yj в процессе подачи на вход сети входного вектора X :
![]() ,
,
где j – номер нейрона.
Нейронную сеть можно представить в виде «чёрного ящика».

Основная задача обучения сети состоит в нахождении значений элементов матрицы весовых коэффициентов W таких, что на некоторый входной вектор будет формироваться правильный выходной вектор. Элементы матрицы W формируются на основе обучающей выборки.
![]()
Персептронные алгоритмы обучения Алгоритм обучения по правилу Хебба
Данный алгоритм положен в основу процесса обучения многих типов нейронных сетей.
Рассмотрим особенности применения правила Хебба к обучению НС.
Рассмотрим НС следующего вида:

![]()

wij – весовой коэффициент связи нейронов i и j.
Предположим, что функция активации в выходном нейроне является пороговой. Для представления пороговой функции используется дополнительный вход с некоторым весовым коэффициентом b. Тогда выходной сигнал НС может быть вычислен следующим образом:
![]() .
.
Процесс обучения НС состоит в настройке коэффициентов межнейронных связей и порогов при подаче на входы НС образов из обучающей выборки. Входной образ представляется в виде вектора X, каждая компонента которого подается на один из входов нейронной сети.
![]()
Значения коэффициентов межнейронных связей и порогов рассматриваемой НС на каждом шаге обучения (t, t+1,…) вычисляются с помощью следующих соотношений:
 (*)
(*)
Различают алгоритм обучения в соответствии с правилом Хебба с учителем и без учителя. При обучении с учителем выходные сигналы НС сравниваются с эталонными значениями. При использовании алгоритма без учителя: реальные сигналы с выхода нейронной сети используются для кластеризации входных образов.
 дискриминантная линия
дискриминантная линия
Таким образом, алгоритм обучения по правилу Хебба сводится к следующей последовательности действий:
Инициализация весовых коэффициентов и порогов случайными значениями, близкими к нулю (чтобы сеть сразу не могла войти в насыщение).
Подача на вход НС очередного входного образа.
Вычисление значения выхода.
Если значение выхода не совпадает с эталонным значением, то происходит модификация коэффициентов в соответствии с формулами (*). В противном случае осуществляется переход к пункту 5.
Если не все вектора из обучающей выборки были поданы на вход НС, то происходит переход к пункту 2. Иначе, переход к пункту 6.
Останов.
Правило Хебба не гарантирует сходимости процесса обучения, то есть ошибка аппроксимации функции нейронной сетью может превышать допустимое значение.
Основной недостаток алгоритма обучения по правилу Хебба заключается в том, что при увеличении размерности n входного вектора сходимость алгоритма уменьшается. При n > 5 трудно гарантировать сходимость.
Данный алгоритм, как правило, используется в качестве некоторого элемента в других алгоритмах обучения. Наиболее предпочтительным является использование правила Хебба в алгоритмах обучения без учителя.
Пример 1. Воспроизвести с помощью НС логическую функцию «ИЛИ». Будем проводить обучение в соответствии с правилом Хебба.
Примем значения сигналов биполярными: 1 и -1.
![]()
В соответствии с правилом Хебба инициализируем работу НС:
![]()
Вычисляем значение коэффициентов на каждом шаге:

![]() ,
,
![]() вычисляются аналогично.
вычисляются аналогично.
Результаты вычислений сведём в таблицу.
-
шаг
x1
x2
x3
y
w11
w21
b
t
t+1
t+2
t+3
t+4
–
-1
1
-1
1
–
-1
-1
1
1
–
-1
-1
-1
-1
–
-1
1
1
1
0
1
2
1
2
0
1
0
1
2
0
1
0
-1
-2
![]()
![]() – дискриминантная линия
– дискриминантная линия
x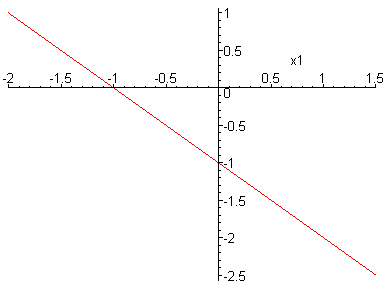
![]()
