Решающие деревья

В искусственном интеллекте широко используются решающие деревья, чаще бинарные.

Решающие деревья представляются в виде многоуровневых НС без обратных связей и могут быть использованы для более эффективного решения задач классификации и распознавания.

Древовидная НС (Tree Neural Network – TNN) – сеть, представляющая собой древовидную структуру (решающее дерево), в каждом узле которого содержится НС.

Пример. Бинарное дерево классификации для разделения образов на три класса.

Основная задача НС – определить оптимальный путь обхода решающего дерева.

Для построения TNN необходимо решить две задачи: первая связана с построением полного решающего дерева, в котором будут учитываться все особенности и условия задачи классификации; вторая – задача редуцирования (отсечение отдельных ветвей), осуществляется путём проверки задачи классификации на непротиворечивость.

Достоинства:

1. уменьшение времени обучения;

2. возможность построения иерархического классификатора;

3. возможность изменения содержимого узлов (НС) на любом уровне дерева.

Методы проектирования нейросетевых архитектур для решения прикладных задач

При решении прикладных задач необходимо решить следующие задачи, связанные с построением НС:

1. задача выбора типа НС;

2. задача выбора алгоритма обучения НС;

3. задача построения топологии (архитектуры) НС.

Первая задача

Основные типы НС:

1. НС с прямым распространением сигнала:

многослойный персептрон:

НС с прямым распространением сигнала являются наиболее применимым типом НС, поскольку для них доказана сходимость алгоритма обучения.

2. НС с обратным распространением сигнала:

Характеризуются небольшой информационной ёмкостью, а также отсутствием универсальной методики, гарантирующей сходимость.

3. НС самоорганизации:

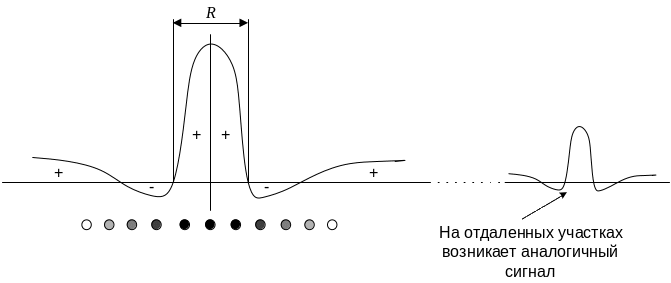
Основные характеристики: алгоритм обучения НС основан на методе конкурентного обучения; в НС данного типа используется механизм латерального торможения.

Метод конкурентного обучения заключается в следующем: фиксируется нейрон с наибольшей активностью, далее – при использовании классического алгоритма – обновляются весовые коэффициенты данного нейрона, при использовании алгоритма, учитывающего эффект латерального торможения – также обновляются весовые коэффициенты соседних нейронов, причём величина изменения весов зависит от расстояния до нейрона победителя.

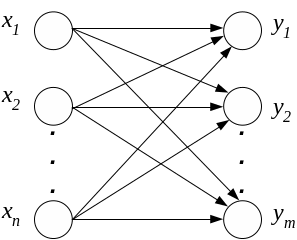
X – входной вектор;

W – вектор весовых коэффициентов.

Основное задача: сопоставить X и W.

Вычисляется вектор W, а затем расстояние от этого вектора до входного. Из всего множества весовых векторов необходимо выбрать такой вектор, расстояние от которого до входного вектора будет наименьшим.

4. Гибридные (комбинированные) сети.

Из существующих типов НС можно составить комбинированную сеть, которая будет обладать нужными качествами.

Вторая задача

Для каждого типа НС существуют свои алгоритмы обучения. Для решения различных задач данные алгоритмы можно подстраивать. Например, для обучения многослойного персептрона вместо алгоритма BP использовать другие методы, такие как квазиньютоновские методы, генетические алгоритмы и прочие. Другой путь связан с подстройкой параметров алгоритмов (скорости обучения, инерционности (для BP), изменение функции активации нейронов классического типа, введение нечетких нейронов).

Третья задача

Задача выбора топологии заключается в определении количества слоёв НС и количества нейронов в каждом слое, которое необходимо использовать для реализации отображения: F: XY. Для обучения используются пары , где p – число распознаваемых классов.

Задача выбора топологии НС состоит в выборе НС с минимальной сложностью S ( ). Обычно сложность НС определяется количеством вычислительных операций, которые надо выполнить для получения выходного сигнала. Данная задача уместна в том случае, когда задано определенное значение ошибки обобщения: . Это задача комбинаторной оптимизации. Если выбрать НС с небольшим количеством слоев и небольшим количеством нейронов каждого слоя, то есть уменьшить сложность, то данная нейронная сеть не сможет обеспечить заданную ошибку обобщения. С другой стороны, если формировать сеть из большого количества слоев и нейронов, то может возникнуть эффект переобучения (эффект «бабушкиного воспитания»): НС хорошо распознает образы из обучающей выборки, но плохо работает с образами реальной среды.

Если задана сложность S, то можно минимизировать ошибку обобщения, подстраивая соответствующие алгоритмы обучения.

Таким образом, задачи нахождения минимальной ошибки обобщения и нахождения минимальной сложности являются взаимопротиворечивыми и не могут решаться одновременно.

Для решения задачи проектирования НС задача оптимизации может решаться в двух постановках:

1. Задана сложность НС, необходимо минимизировать ошибку обобщения.

2. Задана , найти НС минимальной сложности.