5. Алгоритм состязания процедур соединения и разделения.

Алгоритм основан на использовании двух процедур: разделяющей и собирающей.

Для работы алгоритма необходимо определить:

• множество векторов X₁, X₂, … , X_n

• число кластеров q

• пропорцию: собирающая процедура : разделяющая процедура

• способ вычисления расстояния между векторами

Алгоритм сводится к следующей последовательности действий:

1. Образование кластерных центров по одному на каждый вектор.

2. Реализация разделяющей процедуры, то есть нахождение двух наиболее удалённых друг от друга элементов. Найденные элементы разделяются таким образом, чтобы к ним нельзя было применить собирающую процедуру.

3. Реализация собирающей процедуры, то есть нахождение двух наиболее близких (ранее не разделённых) друг к другу элементов. Найденные элементы объединяются в один кластер.

4. Применение собирающей и разделяющей процедур осуществляется в соответствии с определённой стратегией. Например, задаётся два интервала (0; 30) и (31; 100). Один из них соответствует собирающей процедуре, другой – разделяющей. На каждом шаге берётся произвольное число из интервала (0; 100), определяется, какому из двух интервалов оно принадлежит, и в соответствии с этим определяется применяемая процедура.

5. Останов, если все входное множество разделено или достигнуто заданное число кластеров q.

Для определения начальных кластерных центров в алгоритмах кластеризации используется метод пикового группирования (the mountain clustering method).

Данный метод предложили Ягер, Филев.

Алгоритм сводится к следующей последовательности действий:

1. Формирование сетки пространства данных. В узлах сетки – кандидаты в центры кластеров (V). В зависимости от количества узлов определяется детальность исследования сетки.

2. Конструируется пиковая функция, определяющая меру плотности размещения векторов во входном пространстве.

(1)

где – входной вектор; – среднее квадратичное отклонение (задаётся).

Каждой точке соответствует своя высота данной функции. Пиковая функция может быть рассмотрена как мера плотности данных, которые группируются около некоторого узла.

3. Выбираются кластерные центры:

1. находится точка-кандидат, для которой значение функции наибольшее, найденная точка соответствует первому кластерному центру ;

2. выбирается следующий кластерный центр: из множества V исключаются узел , а также узлы, находящиеся в непосредственной от него близости. Для этого вычисляется:

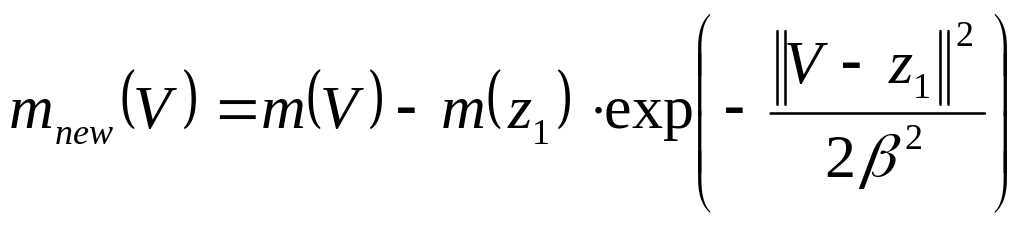
где – эмпирический коэффициент; – центр исключенного кластера.

4. Вновь выбирается кластерный центр, для которого значение функции наибольшее.

5. Останов, если найдено заданное число кластерных центров.

Сети адаптивного резонанса

Одна из основных проблем человеческого восприятия – это проблема стабильности-пластичности. При поступлении некоторой новой информации перед человеком возникает дилемма: относится ли эта информация к новому образу либо она представляет вариант старой, уже знакомой ситуации, её не требуется запоминать. Таким образом, память должна оставаться пластичной, способной к восприятию новых образов и в то же время сохранять стабильность, гарантирующую неразрушение старых образов.

Сети Кохонена не в состояние отделить новые образы от искаженных или зашумленных версий старых образов. Невозможно выделить новый класс среди существующих.