Алгоритм нечётких k-средних (fuzzy c-means clustering)
Алгоритм предложен американским учёным Bezdek.
Fuzzy ISODATA
Т
вёрдые
алгоритмы С-means
(CM)
Hard C- means (HCM)
Основу алгоритма HCM составляет введение некоторой функции качества при заданных ограничениях.
Пусть U – матрица, определяющая принадлежность множества векторов X некоторым кластерам.
X1, X2, … , Xn – вектора множества X
q – число кластеров
Размерность матрицы U:
X |
q |
||||||
1 |
2 |
………………………… |
q |
||||
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
2 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
… |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
n |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
,
,
Общие ограничения:
1)
(1)
2)
(2)
3) ЦФ:
,
(3)
Рассмотрим вариант нечёткой кластеризации:
Матрица принадлежности U может иметь следующий вид:
X |
q |
|||||
1 |
2 |
…………… |
(q-1) |
q |
||
1 |
0,1 |
0,2 |
0,08 |
|
0,3 |
0,5 |
2 |
0,3 |
|
|
0,02 |
0,42 |
|
… |
|
|
|
|
|
|
k |
0,1 |
0,4 |
|
|
|
0 |
… |
|
|
|
|
|
|
n |
0,001 |
0,08 |
|
|
|
0,9 |
Принадлежность векторов кластеру в
случае нечёткой кластеризации может
находиться в интервале:
.
Вектор может относится к различным кластерам с разной степенью принадлежности (grade), но ограничение (1) остаётся справедливо.
Формула (3) сохраняется, а m изменяется
в интервале:
.
Основная цель кластеризации: подбор центров Z1, Z2, … Zq с целью удовлетворения показателю (3) с учётом ограничений (1) и (2).
Для оптимизации целевой функции (3) Bezdek ввёл функцию Лагранжа:
(4)
Bezdek доказал, что минимизация функции (4) осуществляется по следующим формулам:
(5)
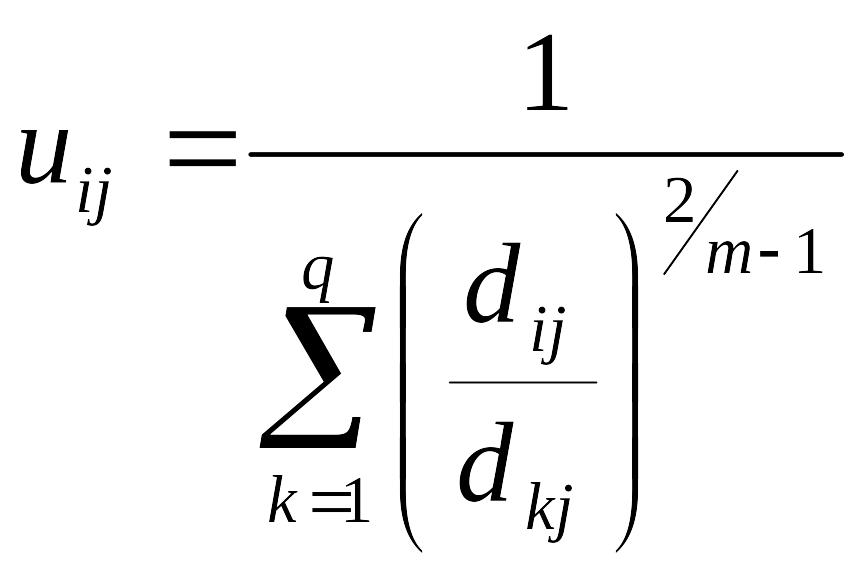(6)
В режиме off –line алгоритм fuzzy C-means сводится к следующей последовательности действий:
Инициализировать матрицу U случайным образом числами в интервале , при этом должны выполняться ограничения (1) и (2).
Вычислить q нечётких кластерных центров по формуле (5).
Вычислить стоимостную функцию по формуле (3).
Останов, если значение целевой функции J окажется ниже заданного порога или её уменьшение на предыдущем шаге ниже допустимого значения. В противном случае вычисляем значения
по формуле (6) и переходим к шагу 2.
Замечание 1. Вместо инициализации матрицы U (шаг 1) могут инициализироваться кластерные центры.
Замечание 2. Алгоритм не даёт гарантии получения оптимального решения, поэтому начальная инициализация центров должна производиться с помощью других алгоритмов или с помощью приёма "мультстарт".