3. Алгоритм внутригруппового среднего (метод k-средних, k-means clustering, c-means clustering)

Данный алгоритм минимизирует сумму квадратов расстояний между точками кластеров в процессе разбиения исходного пространства на q кластеров.

Дано:

1. множество точек во входном пространстве X

Алгоритм сводится к следующей последовательности действий:

1. Произвольно выбираются q центров кластеров (в качестве центров кластеров берутся точки из входного множества).

2. Все образы (точки из входного множества), не являющиеся центрами кластеров, «разносятся» по кластерам в соответствии с принципом минимального расстояния до центра кластера.

Образ х принадлежит кластеру K_j, если расстояние от точки х до центра z_j(r) данного кластера меньше расстояния от х до центра любого другого кластера (q-1). K_j определяет множество, состоящее из точек, включённых в него до r-ого шага.

, если

3. Определяются новые центры кластеров z_j(r+1), j=1… q таким образом, чтобы минимизировать показатель качества J.

В данном случае используется евклидово расстояние.

Новый центр кластера вычисляется по следующей формуле:

, где – количество точек, включенных в пространство K_j к r-ому шагу итерации.

4. Алгоритм заканчивает свою работу, если выполняется равенство: 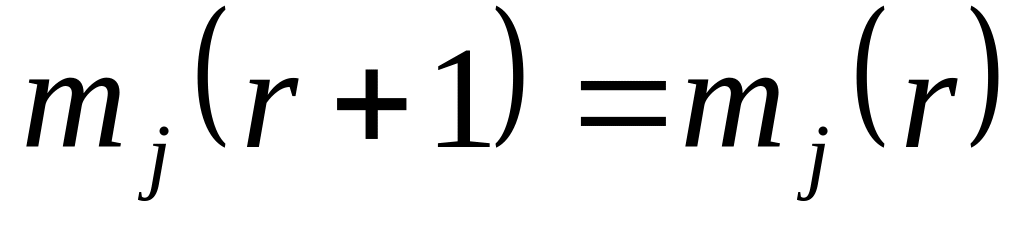, то есть не изменяются центры кластеров. В противном случае, переход к пункту 2.

Пример реализации алгоритма К-средних

Дано:

Х={x₁, x₂,…,x₁₀}

q=3

Положим, что Z₁ = X₁; Z₂ = X₃; Z₃ = X₄

В технике оптимизации используется приём "мультстарт": алгоритм оптимизации реализуется несколько раз из различных начальных точек, а затем из полученных решений выбирается наилучшее.

Шаг 1. Определяем минимальное расстояние от каждой точки до каждого кластера.

	X1	X2	X3	X4	X5	X6	X7	X8	X9	X10
коорд.	(2;2)	(2;4)	(3;4)	(3;8)	(4;7)	(5;9)	(6;1)	(6;8)	(7;1)	(8;1)
Z1	0	2	-	-	5,4	7,6	4,1	7,2	5,1	6,05
Z2	-	1	0	-	3,2	5,4	4,2	5	5	5,8
Z3	-	4,1	-	0	1,4	2,3	7,6	3	8,05	8,6

Шаг 2. По критерию минимального расстояния определяем, какие точки относятся к какому кластеру.

кластер	точки
1	X1, X7
2	X2, X3, X9, X10
3	X4, X5, X6, X8

Шаг 3. Пересчёт всех кластерных центров Z_i

Z₁ = (4; 1,5)

Z₂ = (5; 2,5)

Z₃ = (4,5; 8)

Шаг 4.

	X1	X2	X3	X4	X5	X6	X7	X8	X9	X10
Z11	2	3,2	2,7	6,6	5,5	7,6	2	6,8	3	4
Z21	3	3,35	2,5	5,85	4,6	6,5	1,8	5,6	2,5	3,4
Z31	3,5	4,7	4,3	1,5	1,1	1,1	7,2	1,5	7,4	7,8

Шаг 5.

кластер	точки
1	X1, X2
2	X3, X7, X9, X10
3	X4, X5, X6, X8

Шаг 6.

Z₁² = (2; 3)

Z₂² = (6; 1,75)

Z₃² = (4.5; 8)

Шаг 7.

	X1	X2	X3	X4	X5	X6	X7	X8	X9	X10
Z12	1	1	1,4	5,1	4,47	6,7	4,47	6,4	5,4	6,3
Z22	4	4,6	3,75	6,9	5,6	7,1	0,75	6,25	1,25	2,1
Z32	6,5	4,7	4,3	1,5	1,1	1,1	7,2	1,5	7,4	7,8

Шаг 8.

кластер	точки
1	X1, X2, X3
2	X7, X9, X10
3	X4, X5, X6, X8

Если проводить дальнейшее разбиение, центры кластеров изменяться не будут.