Алгоритмы кластеризации

В настоящее время существует довольно большое число алгоритмов кластеризации, которые можно использовать для нахождения кластерных центров.

Основная идея кластерных алгоритмов – разделение входного пространства на группы. При этом сходство векторов внутри группы должно быть больше сходства с векторами других групп. Для реализации этой идеи вводятся метрики схожести. Большинство из них чувствительны к интервалу изменения входных переменных, поэтому входные переменные нормализуются и приводятся к единичному интервалу.

1. Пороговый алгоритм

Дано:

1. множество точек во входном пространстве X

;

2. пороговая величина Т, определяет критерий принадлежности точки какому-

либо классу (кластеру).

Данный алгоритм сводится к следующей последовательности действий:

1. Выбираем случайным образом точку, соответствующую центру первого кластера. (z₁)

2. Из множества точек входного пространства X выбираем произвольную точку x_i и вычисляем расстояние от данной точки до центра первого кластера z₁. ( )

3. Если выполняется неравенство , то точка x_i принадлежит кластеру с центром z₁. В противном случае, создаётся новый кластер с центром z₂= x_i.

4. Пункты 2 и 3 циклически повторяются для всех точек множества X.

Если точки множества X расположены на значительном расстоянии друг от друга, то в результате работы данного алгоритма для каждой точки будет создан свой кластер.

Недостаток алгоритма: Эффективность алгоритма во многом определяется величиной

пороговой величины Т и зависит от порядка просмотра точек множества X.

2. Алгоритм максимального расстояния

Характерная особенность алгоритма – выбор наиболее удалённых кластеров.

Дано:

1. множество точек во входном пространстве X

Данный алгоритм сводится к следующей последовательности действий:

1. Выбираем случайным образом точку, соответствующую центру первого кластера. (z₁)

2. Из множества точек X выбираем такую точку, которая наиболее удалена от точки, соответствующей центру z₁, и определяем эту точку как центр второго кластера.

3. Для каждой из точек 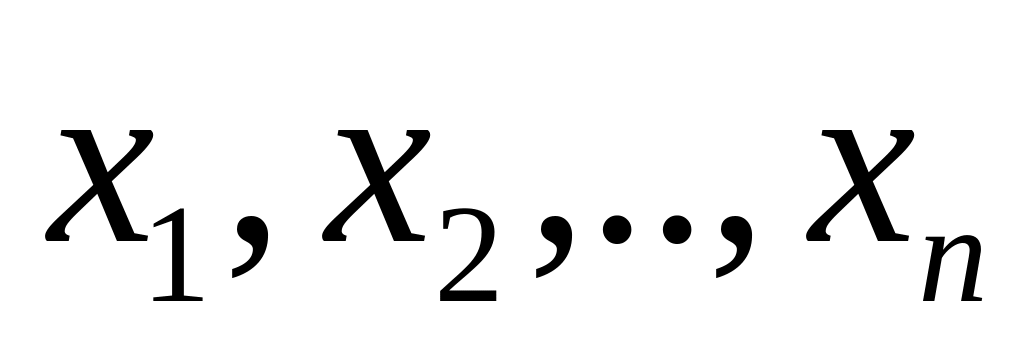вычисляются расстояния от данной точки до всех центров кластеров 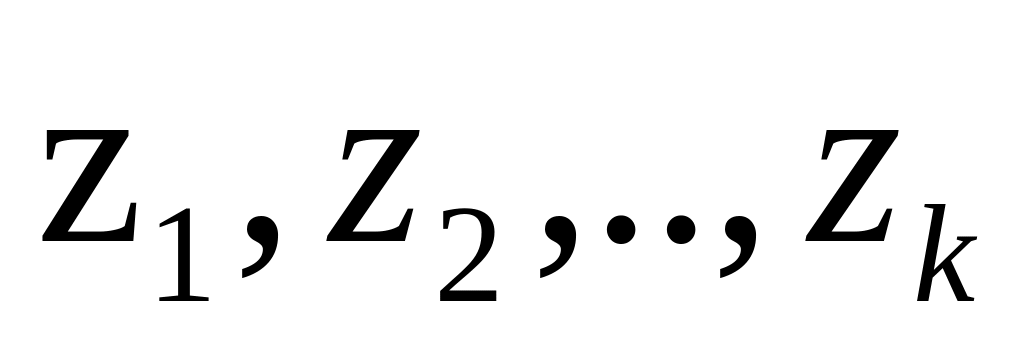, созданных на данный момент времени.

То есть для каждой точки x_j множества X определяется кластер («свой» кластер), расстояние до которого будет минимальным. Далее выбирается точка x^*, наиболее удалённая от данного («своего») кластера.

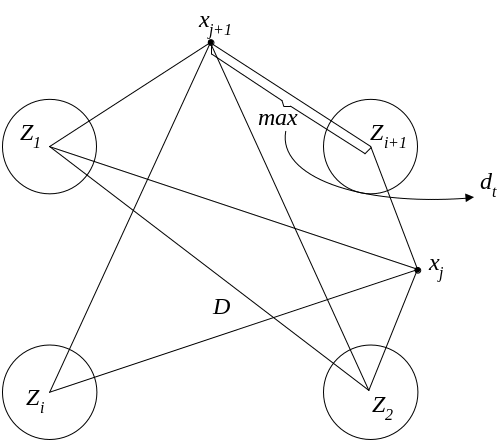
На каждом шаге алгоритма t=1,2,3,…вычисляется величина:

Если значение d составляет существенную часть (не менее половины) от величины , то тогда x^* объявляется центром нового кластера. В противном случае (значение d менее половины от величины ) процесс завершается, а все оставшиеся точки множества X разносятся по ближайшим кластерам.

Недостатки алгоритма:

2. случайный выбор начального кластера

3. увеличение уровня сложности на каждом шаге работы алгоритма