Применение сети Хопфилда к решению задач комбинаторной оптимизации
Рассмотрим задачу коммивояжера (классический пример NP-полной задачи):
На плоскости расположено N городов (в данном случае N=5). Необходимо, начиная с произвольного города, посетить все города, при этом в каждом побывать ровно один раз. Проблема заключается в выборе маршрута с минимально возможной длиной пути.
Для решения этой задачи может быть
использована сеть Хопфилда, состоящая
из
нейронов, расположенных в виде матрицы
нейронов: i-я строка
матрицы соответствует i-му городу
(одному из A, B, C,
D, E),
i-й столбец соответствует i-му
порядку посещения города. Выход узла
сети на пересечении строки x (A, B,
C, D,
E) и столбца i
обозначим
,
где x представляет город, а i –
порядок посещения. Тогда один из
возможных путей имеет вид:
.
Зачерченные
и светлые
кружки обозначают выходы узлов
соответственно. Если
,
то это означает посещение города x
на шаге i. Поскольку каждый город
может быть посещён только один раз, то
в матрице нейронов в каждом столбце и
в каждой строке должно быть только по
одному зачерченному кружку, соответствующему
единичному выходу.
Расстоянием между городами x
и y является :
,
где
.
Целевая функция E задачи поиска оптимального маршрута (функция энергии) может быть определена следующим образом:
(1)
, где
;
- положительные константы.
Первые три слагаемых вводятся для определения правил синтаксиса задачи. Необходимо минимизировать функцию цели, т.е. E должна быть равна 0, следовательно, все слагаемые должны быть равны 0.
,
если имеется только один активный
нейрон в каждом ряду, т.е. если каждый
город посещается только один раз в
каждом туре, иначе
.
,
если имеется только один активный
нейрон в каждом столбце, т.е. в каждый
момент времени посещается только один
город.
определяет посещение N
заданных городов в каждом туре. Таким
образом, первые три слагаемых уравнения
отвечают за допустимость маршрута:
каждое из этих слагаемых обращается в
нуль на допустимых маршрутах и принимает
значение больше нуля на не допустимых.
Четвёртое слагаемое минимизирует длину маршрута. Отрезок пути между двумя городами включается в сумму только тогда, когда один из городов является относительно текущего города x либо предыдущим, либо последующим.
Приведём целевую функцию к основной форме уравнения сети Хопфилда – функции Ляпунова для двумерной нейронной матрицы:
.
(2)
Путём сопоставления коэффициентов уравнения (1) и (2) можно определить весовые коэффициенты:
,
где
при
- в противном случае.
Теперь алгоритм обучения Хебба можно заменить прямым заданием указанных весов для НС.
Сеть Хемминга
Сеть Хемминга (Hamming) – расширение сети Хопфилда. Данная сеть, по сравнению с сетью Хопфилда, характеризуется меньшими затратами на память и объемом вычислений, что очевидно из её структуры. Сеть состоит из двух слоев, каждый из которых имеет по m нейронов, где m – число образов.
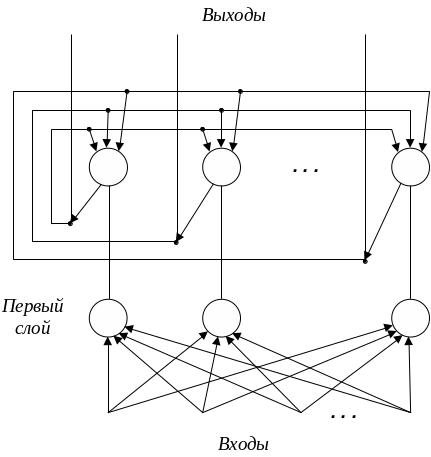
Идея работы сети состоит в нахождении расстояния Хемминга от тестируемого образа до всех образов.
Расстояние Хемминга – число отличающихся битов в двух бинарных векторах.
Сеть должна выбрать образ с минимальным расстоянием Хемминга до неизвестного входного сигнала, в результате чего будет активизирован только один выход, соответствующий этому образу.
Функция активации сети является пороговой линейной.
Значение F должно быть достаточно большим, чтобы любые возможные значения аргумента не приводили к насыщению.
Алгоритм функционирования сети:
Инициализация сети: весовым коэффициентам первого слоя и порогу активационной присваиваются следующие значения:
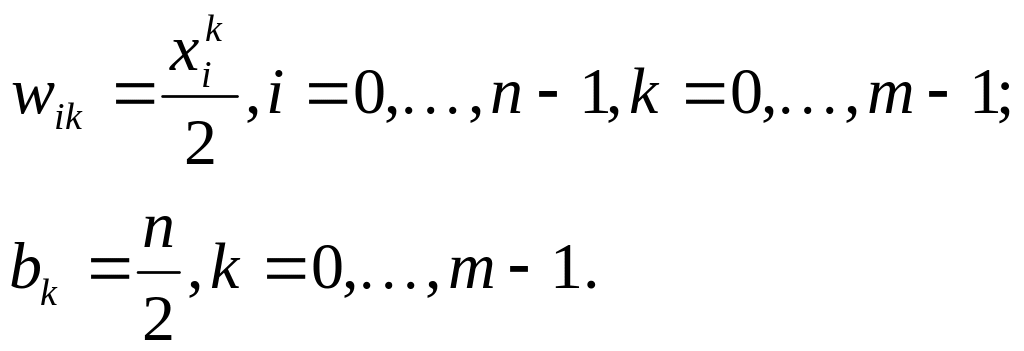
Здесь
i-тый элемент k-того образа.
Весовые коэффициенты тормозящих связей
во втором слое принимают равными
некоторой величине
.
Связь входа нейрона с его выходом имеет
вес +1.
Подача на входы сети неизвестного входного вектора X=
,
исходя из которого рассчитываются
состояния нейронов первого слоя
(верхний индекс в скобках указывает
номер слоя):
.
После этого полученными значениями инициализируются значения выходов второго слоя:
.
Вычисление новых состояний нейронов второго слоя:
и значения их выходов:
,
где t – номер текущей итерации.
Проверить, изменились ли выходы нейронов второго слоя за последнюю итерацию. Если да – перейти к п.3, иначе – останов.
Преимущества сети Хемминга над сетью Хопфилда:
сеть Хемминга способна найти минимальную погрешность, если погрешности входных бит являются случайными и независимыми;
для функционирования сети Хемминга нужно меньшее количество нейронов;
сеть Хемминга не страдает от неправильных классификаций;
сеть Хемминга быстрее и точнее, чем сеть Хопфилда.