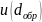5.4 Толщина, d

Стандартная неопределенность толщины образца включает в себя три вклада:

5.4.1 Вклад из-за различия в толщинах пленки в пределах образцов u(d_обр), который определяется по формуле (5). Где рассчитывается по формуле (4)

Тип оценивания неопределенности: А. Вид распределения: нормальное

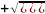
5.4.2 Вклад из-за погрешности измерения толщины образцов u(d_изм). Пределы допускаемой погрешности измерения по отсчетному устройству шкалы скобы рычажной в соответствии с ГОСТ 11098 для отсчета в пределах более, чем 30 делений, составляют 1,4 мкм. Предполагая прямоугольное распределение этой погрешности в границах ее предельных значений, найдем количественную оценку стандартной неопределенности, обусловленную погрешностью измерения толщины образцов:

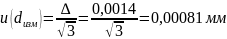
5.4.3 Вклад из-за ошибки оператора при снятии показаний со шкалы средства измерений

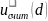
Цена деления используемой для измерений толщины пленки рычажной скобы СРП-25 составляет 0,001 мм. Поэтому предполагается, что величина ошибки оператора будет иметь прямоугольное распределение в пределах 0,0005 мм. Тогда значение стандартной неопределенности, обусловленной ошибкой снятия показаний со шкалы рычажной рассчитываем как:

Суммарную стандартную неопределенность толщины пленки найдем по формуле:

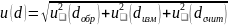
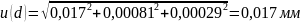
5. Растягивающая нагрузка в момент разрыва Fr

Стандартная неопределенность толщины образца включает в себя два вклада:

5.5.1 Вклад из-за различия в измерениях силы пленки, который определяется по формуле (6). Где рассчитывается по формуле (2). Тип оценивания неопределенности: А. Вид распределения: нормальное

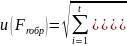(6)

5.5.2 Вклад из-за погрешности измерения силы . Неопределенность растягивающей нагрузки возникает из-за погрешности ее измерения с помощью разрывной машины. В соответствии с ГОСТ 14236 предел допускаемого значения погрешности измерения нагрузки при прямом ходе не должен превышать ±1 % измеряемой нагрузки. Предполагая прямоугольное распределение. При этом, неопределенность растягивающей нагрузки определяется:

Примечание: т.к. измеритель силы имеет цифровое устройство, то неопределенность считывания оператора принимаем равном нулю.

Стандартная неопределенность измерения растягивающей нагрузки определим по формуле:

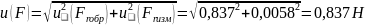
6 Рассчитаем коэффициенты чувствительности

6.1 Коэффициент чувствительности для растягивающей нагрузки

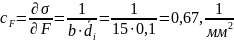
6.2 Коэффициент чувствительности для толщины образца

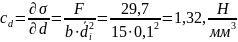
6.3 Коэффициент чувствительности для ширины образца

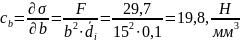
В таблице 2 представлен бюджет неопределенности

Таблица 2 – Бюджет неопределенности

Величи-на	Тип оценивания неопреде-ленности	Вид распределения	Стандартная Неопределен-ность	Коэффи-циент чувстви-тельности	Вклад в неопределен-ность
	А	нормальное	0,837 Н	0,67, 1/мм2	0,56, Н/мм3
	B	прямоугольное	0,0058 Н	0,67, 1/мм2	0,004, Н/мм3
	A	нормальное	0,0017 мм	19,8, Н/мм3	0,0336, Н/мм3
	B	прямоугольное	0,00081 мм	19,8, Н/мм3	0,016, Н/мм3
	B	прямоугольное	0,00029 мм	19,8, Н/мм3	0,006, Н/мм3
	B	прямоугольное	0,01 мм	1,32, Н/мм3	0,0132, Н/мм3

На рисунке 3 представлена диаграмма влияния составляющих u(F_r), u(d), u(b) на суммарную стандартную неопределенность u(σ_r).

u,%

Рисунок 3 – Диаграмма влияния составляющих u(F_r), u(d), u(b) на суммарную стандартную неопределенность u(σ_r).