Расфокусировка оптических систем
В результате отступления фокусных расстояний компонентов схемы от расчетных значений и вследствие погрешностей их продольной установки при сборке возможно появление расфокусировки оптической системы Δz.
Допустимая расфокусировка определяется назначением системы. Так, для проекционной системы допустимое значение Δzдоп лимитируется диаметром кружка рассеяния, определяющим предел допускаемой степени нерезкости. Для оптических систем, работающих совместно с глазом, Δzдоп определяется шириной аккомодации глаза (для оптических систем без сетки). Поскольку предел аккомодации глаза составляет 0...4 дптр (или от ∞до 250 мм), то область резкой видимости без сетки начинается в переднем фокусе окуляра и кончается на расстоянии 4f”ok /1000 от фокуса.
Например, при f”ok = 20мм:
В каждом конкретном случае величину Δzдоп определяют особо, исходя из требований к оптической системе.
Расфокусировка двухкомпонентной оптической системы. Представлена оптическая схема, состоящая из двух компонентов, переносящих изображение из плоскости I сопряженную с ней плоскость II. При сборке такой системы возможны продольные ошибки установки компонентов оптической системы и плоскости I, в результате чего плоскость изображения II смещается от расчетного положения на Δz. Введя модуль перемещения компонентов и, через который можно выразить смещение компонентов (ошибку) в виде произведения kjm, где kj-некоторый постоянный коэффициент, определим расфокусировку системы Δz в виде функции параметров оптической системы x0, d0, f1 , f2, х20, а также смещений kjm. (k0m — смещение плоскости предметов I, k1m и k2m — смещения 1-го и 2-го оптических компонентов соответственно).
В телескопических системах под фокусировкой понимают установку сетки в фокальной плоскости объектива. При предварительной установке сетки в фокусе окуляра точность фокусировки зависит от точности совмещения локальных плоскостей объектива и окуляра (установки нуля диоптрий).
Часто в оптических системах в местах промежуточных изображений устанавливают сетки. В этих случаях неточность фокусировки не только влияет на правильность диоптрийной установки, но и вызывает параллакс сетки прибора.
Лекция №6.
Связь фпм и фрл объективов с децентрировкой и расфокусировкой ос. Измерение передаточных функций ос фотоэлектрическим способом. Приёмы комплектации компонентов высокоточных объективов перед сборкой.
Децентрировку можно уменьшить до допустимой величины, если линзу в оправе на специальном центриро- вочном патроне смещать и разворачивать таким образом, чтобы центры кривизны ее поверхностей совместились с осью вращения шпинделя токарного станка, после чего обработать базовые поверхности оправы. При этом оптическая ось линзы совмещается с геометрической осью оправы с требуемой точностью.
Рассмотрим схематически процесс центрирования линзы. На рисунке изображена линза, установленная в центрировочном патроне. Линза установлена так, чтобы центр кривизны наружной поверхности линзы О1 был рас- положен в одной плоскости с центром кривизны О сфери- ческой части патрона. Центры кривизны поверхностей линзы О1 и О2 смещены относительно оси шпинделя станка и при вращении шпинделя описывают окружности. Смещения центров кривизны с оси вращения шпинделя наблюдают и измеряют с помощью автоколлимационной центри- ровочной трубки ЮС-13, разработанной А. А. Забелиным. Трубку укрепляют на задней бабке токарного станка. Вращением винтов 1, расположенных через 90° вокруг оси шпинделя, подвижную часть патрона смещают в плоскости, перпендикулярной к оси шпинделя, так, что центр кривизны линзы О1 совмещается с осью шпинделя . Биения центра кривизны О1 при вращении шпинделя в этом случае не наблюдается, биение центра кривизныО2 увеличивается. Вращением винтов 2, перемещающих сферическую часть патрона, центр кривизны О2 совмещают с осью шпинделя (рис. 1). При этом центр кривизны О1 не смещается с оси шпинделя, так как он был расположен в одной плоскости с центром сферической части патрона. При вращении шпинделя биение обоих центров кривизны линзы отсутствует. В результате оправа линзы будет иметь перекос, но оптическая ось о
линзы будет совмещена с осью шпинделя. Вызванный юстировкой перекос оправы устраняют проточкой резцом 3 ее торца и наружной поверхности, не снимая- линзы с центрировочного патрона. Наружную поверхность оправы линзы с Ø 20** протачивают до размера, равного диаметру корпуса объектива, с минимально необходимым зазором (порядка 0,01 мм).
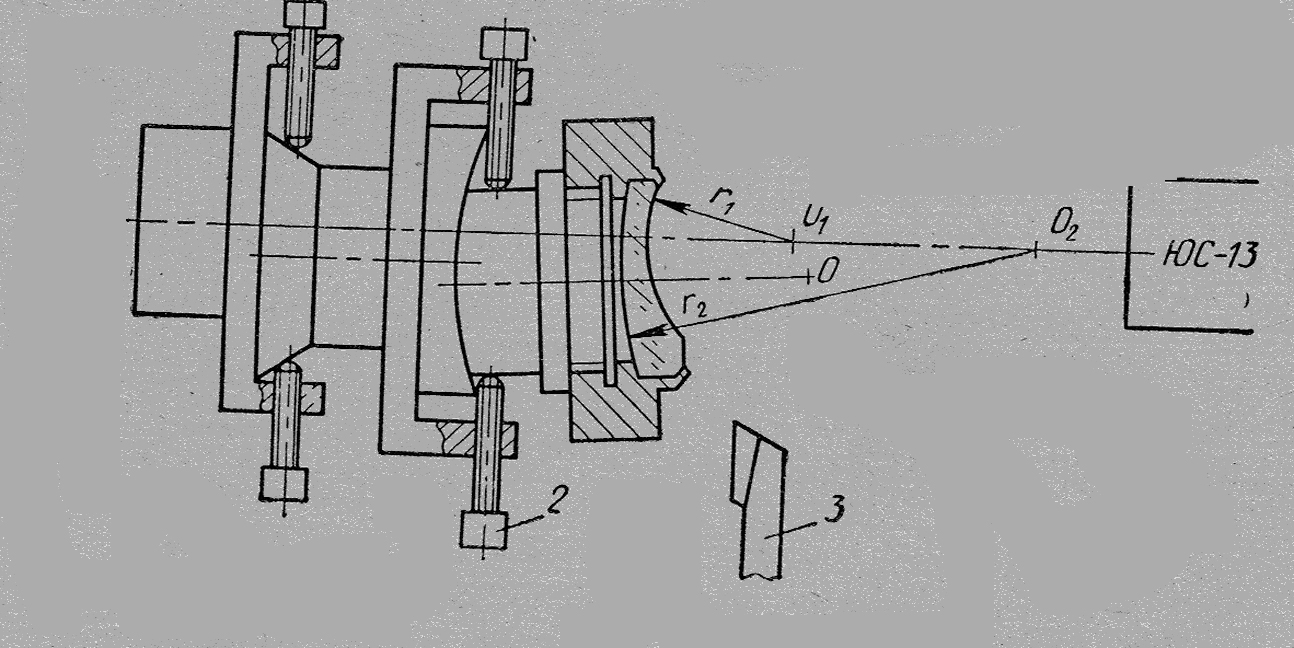
Рис. 1 Центрирование линзы.
Торец оправы подрезают так, чтобы можно было выдержать указанный на чертеже линзы размер 0,54 ± 0,01 мм (см. рис. 2).
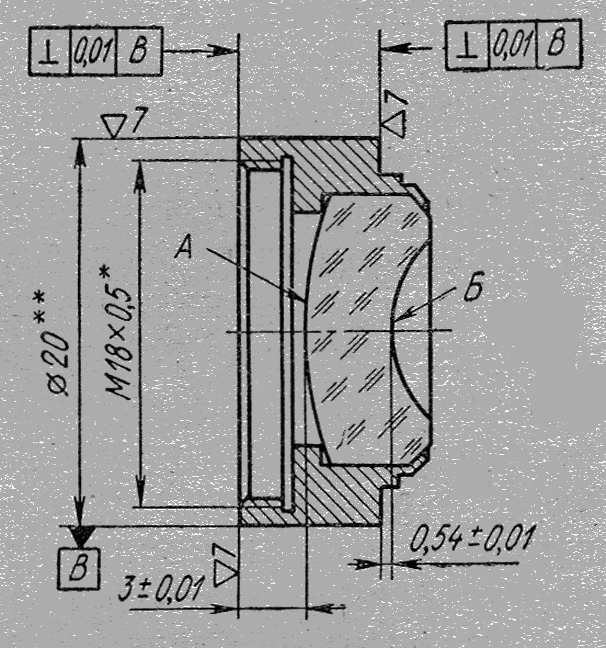
Рис. 2 Пример чертежа линзы для автоколлимационной сборки.
Расстояние от линзы до торца при подрезке измеряют индикаторным приспособлением. Затем линзу снимают с центрировочного патрона и устанавливают в цанговый патрон токарного станка на обработанные базовые поверхности. Подрезают второй опорный торец оправы таким образом, чтобы выдержать размер 3 ± 0,01 мм до второй поверхности линзы. Процесс центрирования линзы окончен.
Оптическая передаточная функция является наиболее полной характеристикой для оценки качества фотографических, проекционных, телевизионных и им подобных объективов. Перечисленные объективы, воспроизводящие оптическое изображение в основ- ном для визуального восприятия, должны обеспечивать передачу крупных деталей с большей резкостью и с большим контрастом, чем очень мелких, близких к пределу разрешения. Это объясняется, прежде всего, тем, что при визуальном рассмотрении художественного снимка, телевизионного или проекционного изображения, уделяется меньше внимания распознаванию мелких дета- лей, чем крупных, и поэтому значительно большую роль играет качество передачи крупных структур предметов. В связи с этим знание того, с какой интенсивностью (амплитудой выходного синусоидального сигнала) и смещением по полю снимка (фазой) передает объектив ту или иную пространственную частоту, характеризующую размер предметов, представляет большой интерес в оценке качества изображения.
Математическое выражение оптической передаточной функции можно получить из уравнения, описывающего процесс образования оптического изображения в частотном представлении:
˜E(Nх ,Ny) = ˜A(Nх ,Ny) ˜L(Nх ,Ny).
Из этого уравнения следует, что преобразование Фурье функ- ции распределения освещенности в изображении отличается от преобразования Фурье функции распределения яркости в предмете коэффициентом˜A(Nх ,Ny), который и назван оптической переда- точной функцией.
Коэффициент изменения амплитуды будет
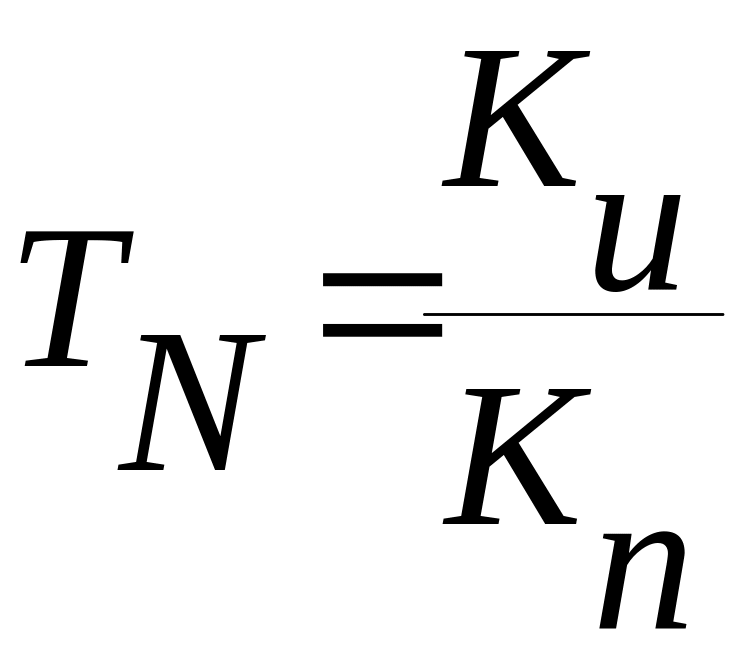
Это отношение называют коэффициентом передачи контраста данной пространственной частоты (или коэффициентом передачи модуляции — КПМ). Изменяя пространственную частоту N, по- лучим зависимость изменения амплитуды от пространственной частоты, т.е. амплитудно-частотную характеристику и зависи мость изменения фазы от пространственной частоты — частотно- фазовую характеристику. Таким образом, амплитудно-частотная характеристика показывает зависимость коэффициента передачи модуляции от пространственной частоты и называется функцией передачи модуляции (ФПМ), или частотно-контрастной характеристикой и обозначается T (N). Зависимость изменения фазы от пространственной частоты называется функцией передачи фазы (ФПФ), или частотно-фазовой характеристикой, и обозначается φ(N). Графическое представление этих характеристик для типового случая дано на рис. 3.
Рис. 3 графики функции передачи модуляции и функции передачи фазы.
Для нулевой пространственной частоты ФПМ имеет максимальное значение и приводится к единице (нормируется), а ФПФ- равна нулю:
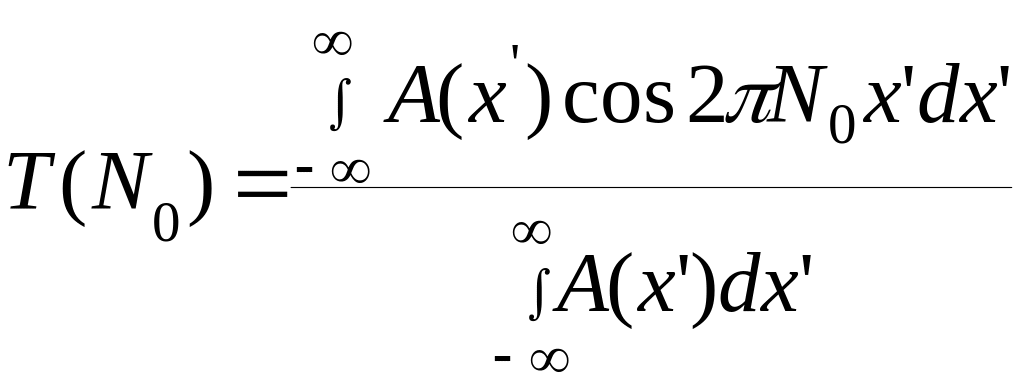
ИЗМЕРЕНИЕ ОПТИЧЕСКОЙ ПЕРЕДАТОЧНОЙ ФУНКЦИИ
Для экспериментального определения оптической передаточной функции, ее модуля (ФПМ) и аргумента (ФПФ) применяют несколько. методов. Все разработанные методы отличаются один от другого использованием различных тест-объектов и способами выделения синусоидальных составляющих. Если оптическую пере- даточную функцию рассматривать как реакцию системы на сигнал синусоидальной формы, то применим прямой метод изме- рения, при котором изображение синусоидального объекта об- разуется исследуемым объективом, а затем измеряется коэффи- циент передачи модуляции и фазовое смещение Коэффициент передачи модуляции (КПМ) пропорционален отношению изме- ренного контраста изображения синусоидального тест-объекта
к контрасту самого тест-объекта. Используя набор синусоидаль- ных тест-объектов с различными пространственными частотами и одинаковым контрастом, можно построить ФПМ, которая яв- ляется функцией параметров объектива и не зависит от контраста изображаемого объекта, поэтому ФПМ обычно измеряют по тест-объектам абсолютного контраста, как наиболее простым в изготовлении. КПМ измеряют следующим образом: синусо- идальный тест-объект 1, выполненный в виде решетки с синусоидальным распределением яркости помещают практической бесконечности или в локальной плоскости объектива коллиматора. Изображение тест-объекта, созданное исследуемым объективом 2, сканируется узкой щелью 3, ширина которой не должна превышать четверть периода ре- шетки. Фотоприемник 4, преобразуя световые сигналы в электрические, передает их на электронный регистрирующий прибор 5, в качестве которого можно использовать микроамперметр, показывающий амплитуду сигнала; или осциллограф, фиксирующий непосредственно сигнал, или самописец. Если контраст решетки равен 1, то амплитуда сигнала на регистраторе пропорциональна КПМ. Устанавливая синусоидальные решетки с различной пространственной частотой, получим значения КПМ для заданных пространственных частот. Кривая, проведенная через точки зна- чений КПМ даст ФПМ).
Фазовый сдвиг в изображении по отношению к тест-объекту можно определить, если на тест-объект нанести специальные контрольные отметки.
Лекция 7