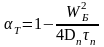- •Порядок расчетов сплавного выпрямительного диода
- •Порядок расчета p- I – n диода.
- •Особенности расчета варикапа.
- •Особенности расчета фотодиода.
- •Особенности расчета диода Шоттки.
- •Образование и емкости плавного, резкого и сверхрезкого p-n перехода. Образование электронно-дырочного (р-n) перехода
- •Резкий несимметричный переход
- •Плавный переход
- •Барьерная емкость р-n-перехода
- •Расчет прямой ветви вах диода.
- •8. Расчет обратной ветви вах диода
- •9. Особенности расчета коэффициента передачи тока базы мощного биполярного транзистора.
- •10. Особенности расчеты частоты отсечки мощного биполярного транзистора
- •12. Порядок расчета сопротивлений базы диодов.
- •13. Порядок расчета сопротивлений базы биполярных транзисторов.
- •14. Расчет паразитных емкостей свч мощных моп транзисторов.
- •17.Особенности расчета порогового напряжения короткоканального моп транзистора.
- •20.Конструкция корпуса мощных свч биполярных транзисторов и требования к используемым материалам.
- •21.Особенности функционирования и расчета пороговых напряжений нормально открытых и нормально закрытых птш.
- •Сравнительный анализ электрических параметров вдмоп, гдмоп и vмоп транзисторов. ( см. Вопрос 23 )
- •Расчет сопротивления сток-исток открытого вдмоп транзистора.
- •Сравнительный анализ электрических характеристик птуп и птш.
- •Особенности расчета порогового напряжения узкоканальных моп транзисторов.
- •Расчет сопротивления сток-исток открытого гдмоп транзистора.
- •Расчет сопротивления сток-исток открытого vмоп транзистора.
- •Расчет выходной мощности, удельного сопротивления и ширина эпитиканального слоя вдмоп транзистора.
- •Расчет толщины подзатворного диэлектрика, концентрации акцептов и минимальной длины канала вдмоп транзистора.
- •3.5 Современные структуры транзисторов
- •Расчет величины подвижности свободных носителей заряда в канале моп транзистора и методы ее увеличения.
- •3.7.1 Подвижность
- •Расчет величин пороговых напряжений моп транзисторов с алюминиевым, n-поликремниевым и p-поликремниевым затворами.
- •3.7.2 Пороговое напряжение классического мопт с большими размерами
- •36. Особенности, за и против применения мощных полевых и биполярных транзисторов.
- •37. Пороговое напряжение и крутизна мощных мопт с двойной диффузией.
- •38. Классификация полупроводниковых диодов.
- •39.Принципы действия, вах тиристоров. Требования, предъявляемые к материалам.
- •41.Конструирование структуры тиристоров.
- •42. Пробой тиристорной структуры.
8. Расчет обратной ветви вах диода
Обратная
ветвь вольт-амперной характеристики
диода с учетом только процесса экстракции
неосновных носителей заряда из прилегающих
к электронно-дырочному переходу областей
соответствует уравнению (1.11). Так как
U < 0, то I
= Isexp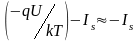 .
Значения токов насыщения для диодов с
толстой и тонкой базой определяются
по формулам (1.13) и (1.14). Так же, как и для
прямой ветви, для обратной необходимо
определить границы температурного
смещения вольт-амперной характеристики
диода, т.е. произвести расчет обратных
токов при Тmin
Tmax
и при комнатной температуре.
.
Значения токов насыщения для диодов с
толстой и тонкой базой определяются
по формулам (1.13) и (1.14). Так же, как и для
прямой ветви, для обратной необходимо
определить границы температурного
смещения вольт-амперной характеристики
диода, т.е. произвести расчет обратных
токов при Тmin
Tmax
и при комнатной температуре.
Кроме
процесса экстракции неосновных носителей
заряда при обратном напряжении на диоде
надо учитывать и процесс тепловой
генерации носителей заряда в
электронно-дырочном переходе. Для
кремниевых диодов ток генерации является
основной составляющей обратного тока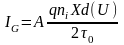 ,
где
,
где
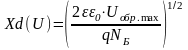 . Расчет генерационной составляющей
обратного тока также необходимо выполнить
для различных обратных напряжений и
для различных температур. Полный обратный
ток через диод определяется суммой
составляющих и зависит от коэффициента
лавинного умножения:
. Расчет генерационной составляющей
обратного тока также необходимо выполнить
для различных обратных напряжений и
для различных температур. Полный обратный
ток через диод определяется суммой
составляющих и зависит от коэффициента
лавинного умножения:
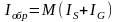 ,
где
,
где
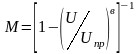 ,
в – эмпирический коэффициент,
равный: 3…5 для кремниевых p+-n
переходов и 2 – для кремниевых n+-p
переходов.
,
в – эмпирический коэффициент,
равный: 3…5 для кремниевых p+-n
переходов и 2 – для кремниевых n+-p
переходов.
9. Особенности расчета коэффициента передачи тока базы мощного биполярного транзистора.
Известно, [1], что коэффициент усиления по току βN можно выразить как
βN
=
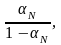
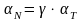 , где
, где
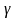 – коэффициент инжекции эмиттера
(эффективность эмиттера);
– коэффициент инжекции эмиттера
(эффективность эмиттера);
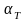 – коэффициент переноса носителей через
базу.
– коэффициент переноса носителей через
базу.
В зависимости от конструкции транзистора и распределения легирующих примесей в эмиттере и в базе для эффективности эмиттера можно написать несколько аналитических выражений
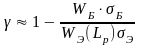 ;
(2.1)
;
(2.1)
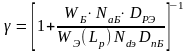 ,
(2.2)
,
(2.2)
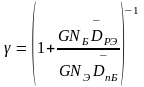 ,
(2.3)
,
(2.3)
где
WБ и WЭ
– ширины электронейтральных базы и
эмиттера, соответственно, NаБ
и NdЭ
– концетрации легирующих примесей в
эмиттере и базе соответственно; DРЭ
и DnБ
– коэффициенты диффузии дырок в эмиттере
и электронов в базе соответственно;
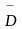 РЭ
и
nБ
– усредненные коэффициенты диффузии;
GNБ и GNЭ
– числа Гуммеля в базе и эмиттере
соответственно; σб и σэ-
электропроводности базы и эмиттера,
соответственно.
РЭ
и
nБ
– усредненные коэффициенты диффузии;
GNБ и GNЭ
– числа Гуммеля в базе и эмиттере
соответственно; σб и σэ-
электропроводности базы и эмиттера,
соответственно.
Если расчет эффективности по первым двум выражениям очевиден, то расчет транзистора с неравномерно легированными базой и эмиттером, т.е. с привлечением чисел Гуммеля в базе и эмиттере GNБ и GNЭ соответственно вызывает затруднение.
Число Гуммеля в базе – это количество примесных атомов на 1 см2 площади квазинейтральной базы WЭ
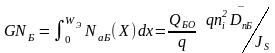 ,
(2.4)
,
(2.4)
где
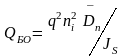 – встроенный заряд в квазинейтральной
области базы,
– встроенный заряд в квазинейтральной
области базы,
DֿnБ – усредненный коэффициент диффузии электронов, JS – плотность тока насыщения коллектора в режиме короткого замыкании на выходе.
Из модели Эберса-Молла для активного нормального режима работы
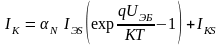 (2.5)
(2.5)
Из
(2.5) видно, что при UЭБ=0
IK=IKS.
На этом построено вычисление значения
необходимое для расчета
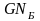 :
:
– строится экспериментальная зависимость плотности тока коллектора в логарифмическом масштабе от напряжения смещения на эмиттерном переходе;
–
точка пересечения экстраполированной
экспериментальной характеристики с
осью тока (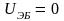 )
дают искомое значение плотности тока
насыщения JS
.
)
дают искомое значение плотности тока
насыщения JS
.
Подставляя
величину JS
в (2.1), находим значение
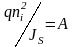 и, следовательно, число Гуммеля в базе
и, следовательно, число Гуммеля в базе
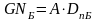 .
Воспользовавшись графиком (рис. 2.1)
предварительно определяем величину
.
Воспользовавшись графиком (рис. 2.1)
предварительно определяем величину
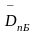 ,
и, зная ее, находим число Гуммеля GNБ.
Зная GNБ и
ширину базы WБ
определяем концентрацию акцепторной
примеси в базе
,
и, зная ее, находим число Гуммеля GNБ.
Зная GNБ и
ширину базы WБ
определяем концентрацию акцепторной
примеси в базе
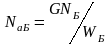 .
По вычисленному значению NаБ
уточняем величину DֿnБ,
возвращаясь к рис. 2.3. Получив новое
значение DֿnБ
вычисляем окончательную величину
GNБ.
.
По вычисленному значению NаБ
уточняем величину DֿnБ,
возвращаясь к рис. 2.3. Получив новое
значение DֿnБ
вычисляем окончательную величину
GNБ.
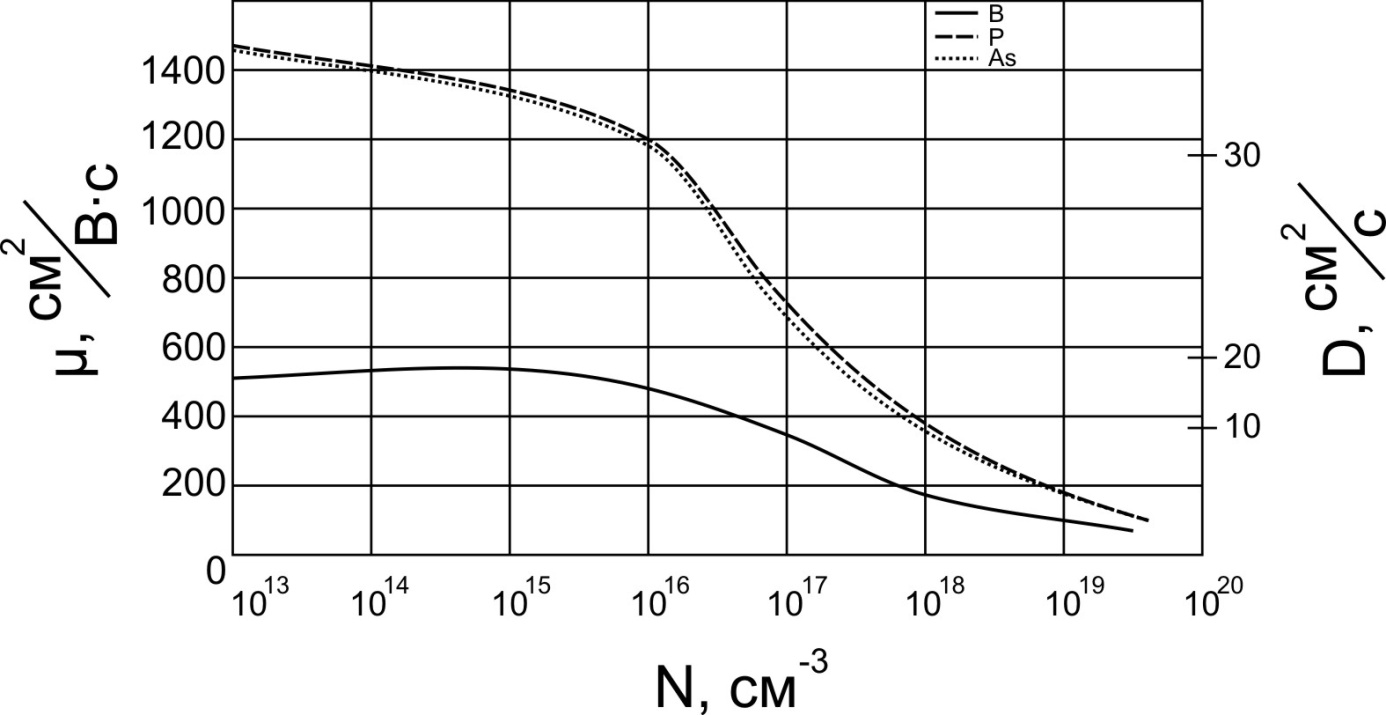
Рисунок 2.3 – Подвижность и коэффициент диффузии электронов и дырок в кремнии при 300К в зависимости от суммарной концентрации примесей [6]
Для
расчета числа Гуммеля в эмиттере
полагаем, что примесная концентрация
меняется там по экспоненциальному
закону с характеристической длиной
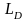 ,
т.е.
,
т.е.
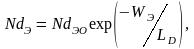 (2.6)
(2.6)
где NdЭО – концентрация примеси в эмиттере на поверхности кристалла; NdЭ – концентрация примеси у края эмиттерной электронейтральной области (х=WЭ) и NdЭО заданы.
Определив
из (2.6) величину
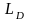 ,
получим интегральную примесную
концентрацию в эмиттере
,
получим интегральную примесную
концентрацию в эмиттере
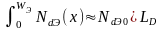 (2.7)
(2.7)
В
сильно легированных эмиттерах (мощные
транзисторы) необходимо вычислять
эффективное число Гуммеля, т.е. необходимо
учитывать эффект сужения ширины
запрещенной зоны, поэтому необходимо
полученное значение Nэ
умножить на величину
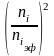 ,
где
,
где
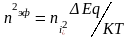 ,
а сужение ширины запрещенной зоны Ед
определить по эмпирическим выражениям
[ 2].
,
а сужение ширины запрещенной зоны Ед
определить по эмпирическим выражениям
[ 2].
Для
расчета коэффициента диффузии в эмиттере
найдем среднюю примесную концентрацию
в нем, разделив эффективное число Гуммеля
для эмиттера на его глубину. По значению
этой величины и рис. 2.3 определим
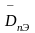 .
.
Обычно допускают, что эффекты сильного легирования уменьшают эффективное число Гуммеля для эмиттера GNЭ до 2 % от интегральной примесной проводимости. Коэффициент переноса носителей через базу αT для транзистора с равномерно легированной базой можно рассчитать по формуле:
αt = Ikn/Idn=1-tnr/τn=1-Ws2/2Dnτn (2.8)
где Iэn и Ikn – электронные токи, входящие в базу и выходящие из нее соответственно; – время пролета через базу носителей заряда при отсутствии в ней электрического поля; Dn – коэффициент диффузии электронов в базе.
В дрейфовом транзисторе с произвольным примесным профилем в базе время пролета tпр определяется следующей формулой:
tnp=[Dnn2
exp(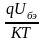 )]-1
)]-1
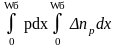 (2.9)
(2.9)
где np – избыточная концентрация неосновных носителей в базе.
В дрейфовом транзисторе с экспоненциальным распределением примеси в базе коэффициент переноса носителей через базу можно рассчитать с использованием дрейфового коэффициента:
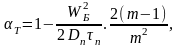
![]() (2.10)
(2.10)
где
m = ln
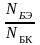 – дрейфовый коэффициент.
– дрейфовый коэффициент.
Для инженерных расчетов коэффициент переноса носителей через базу αT в дрейфовых транзисторах обычно определяется удваиванием в формуле (2.8) коэффициентa диффузии, указывая тем самым на наличие электрического поля в базе.