
- •Порядок расчетов сплавного выпрямительного диода
- •Порядок расчета p- I – n диода.
- •Особенности расчета варикапа.
- •Особенности расчета фотодиода.
- •Особенности расчета диода Шоттки.
- •Образование и емкости плавного, резкого и сверхрезкого p-n перехода. Образование электронно-дырочного (р-n) перехода
- •Резкий несимметричный переход
- •Плавный переход
- •Барьерная емкость р-n-перехода
- •Расчет прямой ветви вах диода.
- •8. Расчет обратной ветви вах диода
- •9. Особенности расчета коэффициента передачи тока базы мощного биполярного транзистора.
- •10. Особенности расчеты частоты отсечки мощного биполярного транзистора
- •12. Порядок расчета сопротивлений базы диодов.
- •13. Порядок расчета сопротивлений базы биполярных транзисторов.
- •14. Расчет паразитных емкостей свч мощных моп транзисторов.
- •17.Особенности расчета порогового напряжения короткоканального моп транзистора.
- •20.Конструкция корпуса мощных свч биполярных транзисторов и требования к используемым материалам.
- •21.Особенности функционирования и расчета пороговых напряжений нормально открытых и нормально закрытых птш.
- •Сравнительный анализ электрических параметров вдмоп, гдмоп и vмоп транзисторов. ( см. Вопрос 23 )
- •Расчет сопротивления сток-исток открытого вдмоп транзистора.
- •Сравнительный анализ электрических характеристик птуп и птш.
- •Особенности расчета порогового напряжения узкоканальных моп транзисторов.
- •Расчет сопротивления сток-исток открытого гдмоп транзистора.
- •Расчет сопротивления сток-исток открытого vмоп транзистора.
- •Расчет выходной мощности, удельного сопротивления и ширина эпитиканального слоя вдмоп транзистора.
- •Расчет толщины подзатворного диэлектрика, концентрации акцептов и минимальной длины канала вдмоп транзистора.
- •3.5 Современные структуры транзисторов
- •Расчет величины подвижности свободных носителей заряда в канале моп транзистора и методы ее увеличения.
- •3.7.1 Подвижность
- •Расчет величин пороговых напряжений моп транзисторов с алюминиевым, n-поликремниевым и p-поликремниевым затворами.
- •3.7.2 Пороговое напряжение классического мопт с большими размерами
- •36. Особенности, за и против применения мощных полевых и биполярных транзисторов.
- •37. Пороговое напряжение и крутизна мощных мопт с двойной диффузией.
- •38. Классификация полупроводниковых диодов.
- •39.Принципы действия, вах тиристоров. Требования, предъявляемые к материалам.
- •41.Конструирование структуры тиристоров.
- •42. Пробой тиристорной структуры.
Резкий несимметричный переход
Переход, в котором область изменения концентрации примесей значительно меньше ширины ОПЗ, называется резким, а если величина этой области больше или равна ширине ОПЗ, — плавным. Первый тип р-n-переходов получают методом эпитаксиального выращивания, второй — диффузиейили имплантацией. Если величина концентрации примеси в одной из областей р-n-перехода значительно превышает концентрацию в соседней, то такой переход называется несимметричным (в отличие от симметричного, у которого Nd = Na).
Зависимости характеристик перехода от координаты (риc. 1 .2) можно получить, решив уравнение Пуассона
|
(1.8) |
где(x) = q(p – n + Nd – Na).
Для идеализированного p-n перхода.
В приближении полного обеднения в ОПЗ отсутствуют свободные носители (x) = q(Nd – Na).
Для области – xр ≤ х ≤0 (рис. 1 .2) запишем:
|
(1.9) |
Полагая, что при x = – xdp и x = – xdn E = – d /dx = 0, находим
|
(1.10) |
Пологая, что при x=– xdр 1 =0 и, что при x= xdn 2 =к , находим
|
(1.11) |
При x = 0 1 = 2 , следовательно,
|
(1.12) |
Используя ( 1 .12) и xd = xdn + xdp, получаем выражение для ширины ОПЗ в состоянии теплового равновесия
|
(1.13) |
Так как обычно Nd>> Na или Na>> Nd, получим
|
(1.14) |
где NБ — концентрация примесей в базе, т.е. в наиболее слаболегированной области р-n-перехода;
xd(0) — ширина обедненного слоя (или ОПЗ), когда напряжение на р-n-переходе U = 0.
а)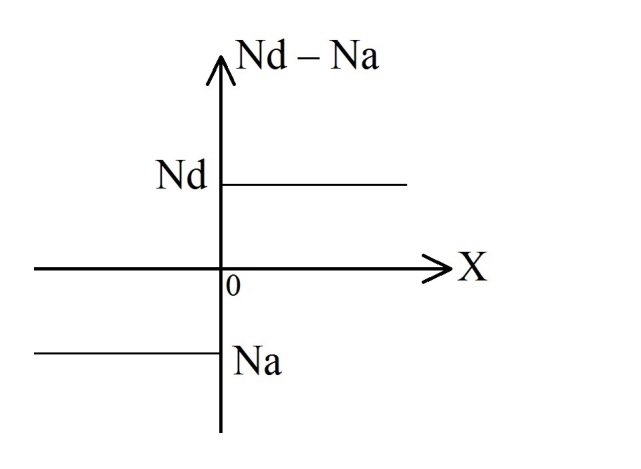 б)
б)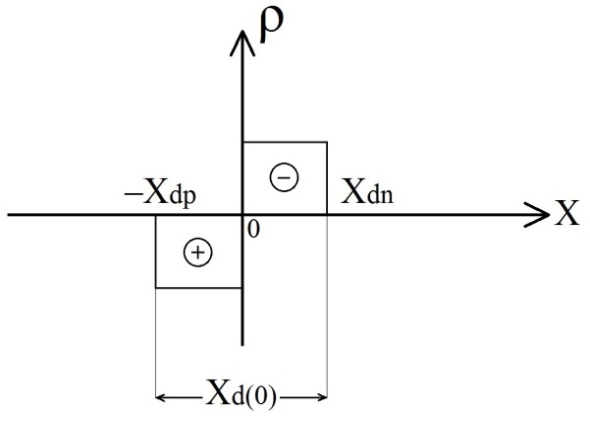
в)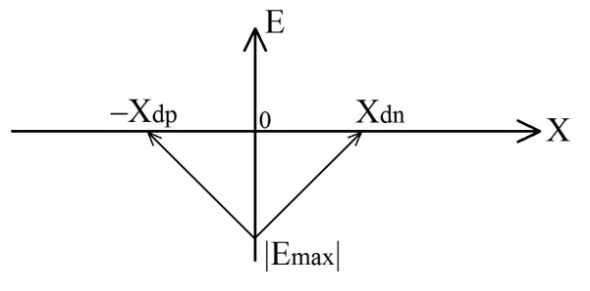 г)
г)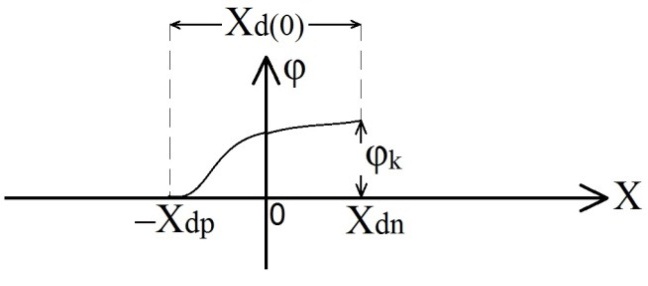
Рисунок 1.2– Характеристики резкого p-n перехода
а — результирующая примесная концентрация;
б — объемный заряд; в —электрическое поле; г — потенциал.
Плавный переход
Общего аналитического решения уравнения Пуассона( 1 .9)для переходов, полученных диффузией или имплонтацией, не существует, поэтому конкретные случаи рассматриваются приближенно. Более точные результаты для этих случаев можно получить численным методом.
В переходе с линейным распределением примеси концентрация во всей области объемного заряда описывается выражением
|
(1.15) |
где а — градиент результирующей примесной концентрации и имеет размерность [см–4].
Распределение напряженности поля и потенциала легко найти для плавного симметричного p-n перехода с линейным распределением примесей из уравнения Пуассона, поскольку плотность объемного заряда в обедненной области зависит от координаты линейно, поле квадратично, а потенциал меняетсякак куб координаты.
Решая
в рамках приближения обеднения уравнение
Пуассона  для обеих областей перехода при граничных
условиях, указанных в подразделе, получим
величины максимального электрического
поля и ширины ОПЗ:
для обеих областей перехода при граничных
условиях, указанных в подразделе, получим
величины максимального электрического
поля и ширины ОПЗ:
|
(1.16) |
|
(1.17) |
Барьерная емкость р-n-перехода
Удельную барьерную емкость р-n-перехода Сjо (Cбар0) можно определить, используя известное выражение Cjo = dQ/dU,
где dQ — дифференциальное приращение плотности заряда, вызванное достаточно малым изменением приложенного к p-n-переходу напряжения.
Следовательно, для несимметричных резких р-n-переходов, принимая Q = qNbxd0 и U = k, выражая величину kиз ( 1 .14), получим
|
(1.18) |
А для плавного р-n-перехода c линейным раcпределением примеcей
|
(1.19) |
Следует отметить, что величина барьерной емкости не зависит от токов, протекающих через р-n-переход. Она связана только c токами смещения. При прямых смещениях р-n-перехода она суммируется c диффузионной емкостью и маскируется при больших плотностях прямого тока диффузионной емкостью.

 ,
, ,а
для области 0 ≤ х ≤ xn,
,а
для области 0 ≤ х ≤ xn,
 .
. и
и 
 .
.
 .
.

 ;
; .
.
 .
.