3.18.Понятие о критической силе для сжатого стержня. Формула Эйлера.

Если упругое тело или конструкция при отклонении от равновесного положения не возвращается к исходному положению, то говорят, что произошла потеря устойчивости.

Явление потери устойчивости упругого тела рассмотрим на примере сжатого стержня.

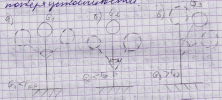
Представим, что на прямой стальной стержень, зажатым одним концом в вертикальном положении, сверху закреплен шаром. При небольшом значении силы тяжести шара G₁, сжимающей стержень, он сохраняет прямолинейную форму и находится в устойчивом равновесии. Если отклонить шар вместе с верхней частью стержня в сторону, то под действием упругих сил стержень, совершив колебание около положения равновесия, снова примет прямолинейную форму. Постепенно увеличивая сжимающую нагрузку путем установления более тяжелых шаров (рис. б), видно, что стержень хоть и сохраняет прямолинейную форму, но при отклонении от положения равновесия возвращается в исходное положение гораздо медленнее, совершая колебания с большей амплитудой. При некоторой нагрузке шара G₃ (рис в) стержень изогнется и проямолинейная форма устойчивого равновесия перейдет в другую криволинейную форму устойчивого равновесия. Если теперь стержень принудительно выпрямить, то он после нескольких колебаний займет равновесное положение в изогнутом состоянии.

Максимальная сжимающая нагрузка, при которой прямолинейная форма стержня устойчива, называется критической силой.

Смысл расчета на устойчивость сжатого стержня заключается в том, чтобы он при некотором значении осевой нагрузки сохранял устойчивую прямолинейную форму и обладал при этом некоторым запасом устойчивости. Коэффициент запаса устойчивости: 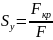. Тогда условие устоичивости сжатого стержня: 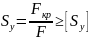— допускаемый коэффициент запаса устойчивости.

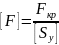— допускаемая нагрузка.

Задачу определения критической силы впервые математически решил Эйлер.

Формула Эйлера:

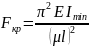
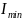— минимальное значение момента инерции площадки поперечного сечения стержня, т.к. потеря устойчивости происходит в плоскости меньшей жесткости.

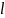—длина стержня.

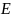—модуль упругости.

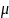—коэффициент приведения длины, т.е. число, показывающее, во сколько раз необходимо увеличить длину шарнирно-закрепленного с обеих сторон стержня, чтобы критическая сила для него была равна критической силе стержня в данных условиях закрепленияя.

3.19.Критическое напряжение. Пределы применяемости формулы Эйлера.

При осевом нагружении стержня в его поперечном сечении возникают нормальные напряжения сжатия, которые возрастают по мере увеличения нагрузки.

Нормальные напряжения, соответствующие критической силе, называются критическими напряжениями: ;

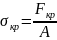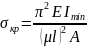
Введем обозначение минимального радиуса инерции сечения:

;

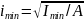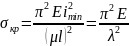
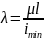— гибкость стержня, она характеризует сопротивляемость стержня потери устойчивости. С увеличением гибкости уменьшается сопротивляемость стрежня потери устойчивости. Гибкость стержня не зависит от материала стержня, а определяется его длиной, формой и размерами сечения.

Определяя значение критической силы, Эйлер исходил из рассмотрения упругой линии изогнутого стержня. Поэтому формула 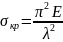справедлива лишь в пределах применимости закона Гука, до тех пор пока критическое напряжение не превышает предела пропорциональности материала стержня.

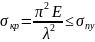
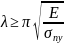
Предельная гибкость материала:

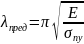
Тогда применимость формулы Эйлера определяется условием:

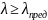
Формула Эйлера применима только в тех случаях, когда гибкость стержня больше или равна предельной гибкости того материала, из которого он изготовлен.

Многие конструкции имеет стержни с гибкостью меньше предельной. Для таких стержней критическое напряжение определяется по формуле Ясинского: ( )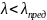

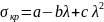
a и b— коэффициенты, зависящие от свойств материала.

С=0,53 для чугунных стержней и с=0 для стальных стержней.