3.11. Напряженно-деформированное состояние при прямом поперечном изгибе.

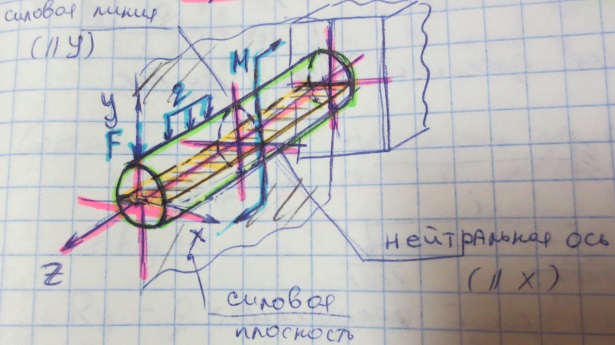
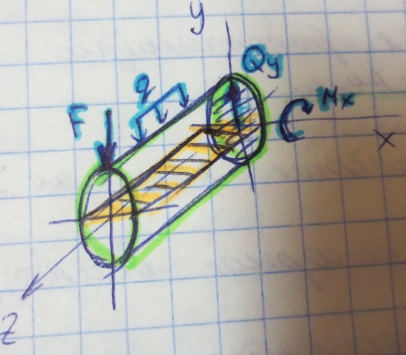
Изгиб- это такой вид деформации бруса при котором в его поперечных сечениях возникают изгибающие моменты. В большинстве случаев одновременно с изгибающими моментами возникают и поперечные силы. Такой изгиб называют поперечным , если поперечные силы не возникают, то изгиб называют чистым.

Плоскость, проходящую через профильную ось бруса (Z) и одну из главных центральных осей его поперечного сечения (Y) называют главной плоскостью бруса. В случае если силовая плоскость, т.е. плоскость действия нагрузок совпадает с одной из главных плоскостей имеет место прямой изгиб бруса, если не совпадает – косой изгиб.

В общем случае прямого изгиба в поперечных сечениях бруса возникает 2 внутренних силовых фактора: поперечная сила (Qy) и изгибающий момент (Mx).

Границей между облостями растяжения и сжатия является слой волокон, который лишь искривляется не испытывая при этом ни растяжения ни сжатия, это так называемый нейтральный слой.

Линия пересечения нейтрального слоя с плоскостью поперечного сечения называется нейтральной осью или нулевой линией.

Брусья работающие на прямой изгиб называются балками.

L

А) простая кансоль:

Б) двухопорная балка:

В) двухопорная балка с одной консолью:

Г) двухопорная балка с 2-ми консолями:

L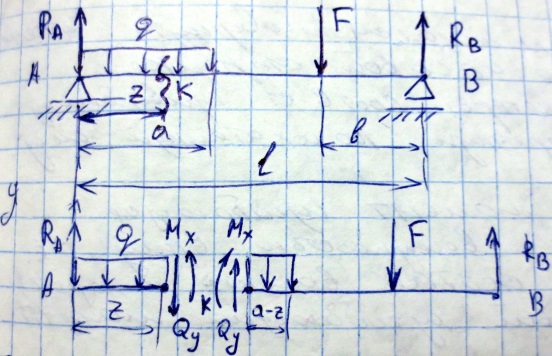 – Расстояние между опорами балки называют пролетом, а длину балки зацепления 1-им концом называют вылетом (рис А)

Обычно брус или балку изображают 1-ой линией лежащую на продольной оси к которой приложены заданные нагрузки. Рассмотрим двухопорную балку (рис.): Считаем, что опорные реакции известны:

Рассмотрим произвольное сечение балки отстоящее на расстоянии Z от опоры А

Составим уравнение проекции на ось Y для определения поперечных сил в левой части: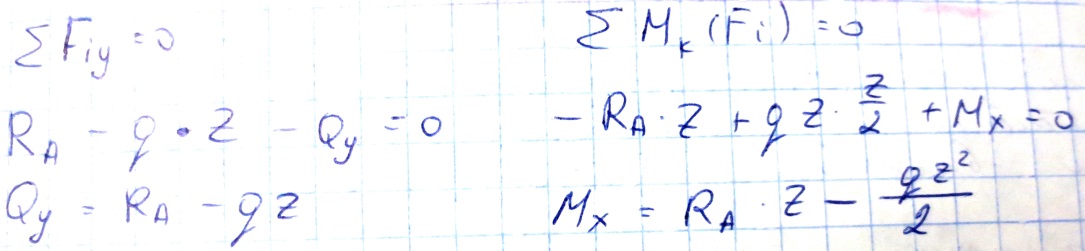

Поперечная сила Qy в произвольном сечении бруса численно равен алгебраической сумме сил приложенных к его отсеченной части.

Изгибающий момент Mx в произвольном поперечном сечении бруса численно равен алгебраической сумме моментов всех внешних сил приложенных к отсеченной части относительно той точки продольной оси бруса через которую проходит рассматриваемое сечение

Правило знаков для построения эпюр Qy и Mx по внешним силам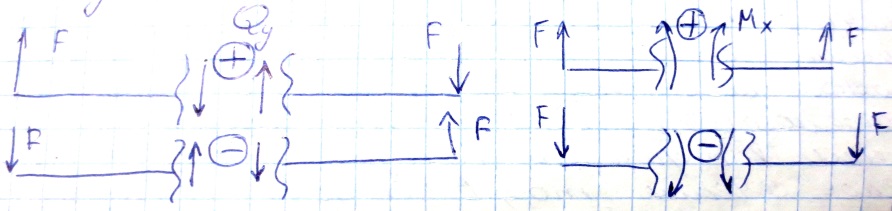

Внешняя сила стремящаяся повернуть отсеченную часть балки по часовой стрелке вокруг той точки оси которая соответствует проведенному сечению вызывает поперечную положительную силу.

Внешняя сила или момент изгибающая отсеченную часть балкт выпуклостью вниз, т.е. таким образом, что сжатые волокна находятся сверху, дает положительный изгибающий момент.

3.12. Условие прочности при прямом поперечном изгибе

Балки рассчитывают на прочность по наибольшим нормальным напряжениям возникающим в их поперечном сечении.

При поперечном изгибе балок на ряду с нормальным возникают и касательные напряжения, но они в основном не велики по сравнению с нормальными и при расчетах на прочность не учитываются, а учитывается нормальное направление.

Qy=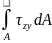 Прочность балки из пластического материала обеспечена, если

Mx=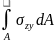 наибольшая по абсолютному значению нормальное напряжение _max возникающая в опасном поперечном сечении не превышает допускаемого [ ]. Для балки поперечные значения которой по всей длине постоянны, то опасное сечение в котором возникает по модулю наибольний изгибающий момент [Mx max]. Наибольшее нормальное напряжение возникает в точках опасного поперечного сечения максимально удаленных от нейтральной оси. Будем называть эти точки опасными. Тогда получим условие прочность в виде: max=( | Mx max| / Ix)*Y max =< [ ]

Где Ix – момент инерции относительно оси Х или осевой момент инерции.

Ymaх- расстояние от опасной точки до нейтральной оси.

В случае, если поперечное сечение балки симметрично относительно нейтральной оси оказывается возможным привести формулу к более удобному виду: Ymax = h/2

Где h – высота сечения или размер в направлении перпендикулярном нейтральной оси.

max=( Mx max / Ix)*( h/2) = Mx max / (Ix*( h/2))= Mx max /Wx

Wx=Ix*( h/2)

Где Wx – осевой момент сопротивления или момент сопротивления при изгибе.

Момент сопротивления – геометрическая характеристика прочности бруса, работающего на прямой изгиб, т.е. чем больше момент сопротивления, тем меньше напряжение возникающего в поперечном сечении при данной нагрузке.

Условие прочности: _max= Mx max /Wx=<[ ]

Это зависимость для проверочного расчета.

Значение моментов сопротивления прокатных профилей приведены в таблицах в соответствии ГОСТов либо справочников.

Рассмотрим моменты сопротивлений простых симметричных сечений:

И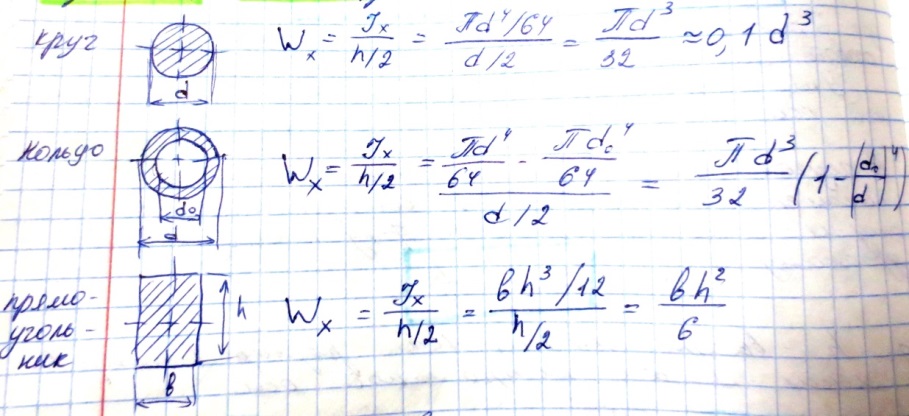 з первого примера видно, что сечение нужно располагать таким обр., что бы силовая линия совпадала с той из главных осей относительно которой момент инерции минимален.