3.8 Условие прочности. Коэффициент запаса. Допускаемые напряжения.

Мех. Испытания позволяют опр-ть те напряж, при которых образец разрушается или имеет заметные пластические деф-ии. Эти напряжения предельные или опасные. Коэффициент запаса прочности – отношение предельного наар к расчетному, возник в элементе конструкции при эксплуатационной нагрузки. 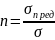>1 Требуемый или нормативный коэф прочности – минимальн необход коэф прочности. Пр-ть элемента конструкции считают обеспеченной, если его расчет коэф запаса не ниже требуемого – условие прочности

- допускаемое напр-ние ; 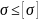В расчетах на пр-ть различают 3 категории напряж. : 1) предельное, при достижении кот появл признаки непосредственного разрушения или возникнов пластических деф-ий. Эти напр-ия зависят от св-в мат-ла и видов деформации. 2) Допускаемые – наиб напр-ие, кот можно допустить в расчетах конструкций. Зависит от мат-ла, вида деф-ии и требуемого коэф запаса проч-ти. 3) расчетное нап-ие – нап-ие, кот возникает в элементе при действии на него нагрузки. Зав-т от его размеров и нагрузок.

3.9 Расчет на прочность стержней при растяжении-сжатии.

Незначительное превышение расчетного нап-ия над допускаемым не опасно, ведь оно составляет лишь часть от предельного. В зависимости от цели расчета различают проверочный, проектный и определение допускаемой нагрузки. Проверочный. Определению подлежит наибольшее расчетн нап-ие, кот сравнивают с допускаемым. Данный расчет применяют при экспертизе выполнения проектов. Условие: 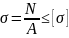, где А-площадь опасного поперечного сечения, Ф – продольная сила, – напряжение в опасном сечении – сеч, в коот коэф запаса пр-ти имеет наименьшее значение приложен наиб нагрузки. При проектном расчете нагрузки и материала(допуск нап-ия) известны и опрдел требуемую площадь сечения бруса 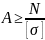В некот случ проводят расчет в форме опр-ния допускаемой нагрузки. Это целесообразно, когда возникает необходимость повышения нагрузки сущ оборудования. Следовательно, надо знать их предельн допуск по условию проч значения. При этом расчете размера бруса и его материала (доп напр) известны. Определению подлежит напр, кот можно допустить при усл пр-ти. При этом расчете опр-ют значение продольной силы. По этому значению с помощью метода сечений опр-ют значение внешних сил.

3.10. Особенности расчета статически неопределимых стержневых систем

Если внутренние силы определились только на основе условий равновесия отсеченные части системы или отдельного бруса, то систему называют статически определимой

Система в которой внутренние силовые факторы, в частности продольные силы не могут быть определены только с помощью метода сечений называют статически неопределимыми системами. => задачи связанные с расчетом указанных систем принято называть статически неопределимыми.

Рассмотрим брус который жестко заделан обоими концами.

В заделках возникают реакции направленные вдоль оси бруса. На брус действует система сил направленных по одной прямой. Статика в этом случае дает одно уравнение проекции на ось, а неизвестных две.

Для решение статически неопределимой задачи надо составить помимо уравнений статики, уравнение перемещений, основанное на рассмотрении деформации системы (геометрическая сторона задачи) и применение закона Гука.

П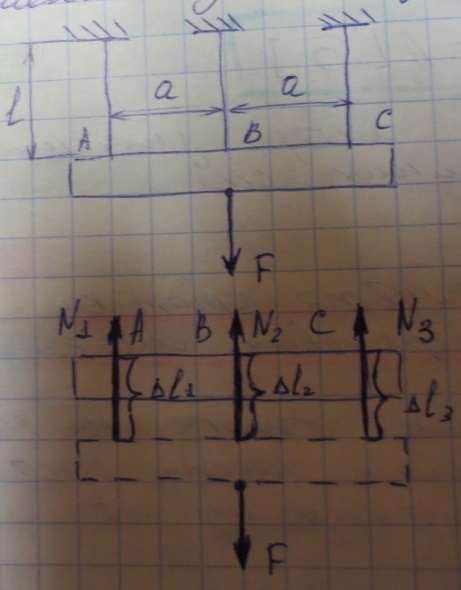 одвешена невесомая весьма жесткая балка нагруженная силой F. Стержни изготовлены из одинакового материала и имеют одинаковое сечение. Для плоской системы параллельных сил статики дает 2 уравнения равновесия. Обозначим реакции действующие на стержни N1, N2, N3, т.е. неизвестных сил 3 и система 1 раз статически неопределима.

. N₁+N₂+N₃-F=0

. -N_1a+N_3a=0

В результате деформации стержней балка займет положение показанное штриховыми линиями. Предположение о высокой жесткости балки позволяет пренебречь её изгибом , а симметрия самой системы и нагрузки приводят к заключению, что все стержни удлиняются одинаково . ΔL₁= ΔL₂= ΔL₃

Если выразить удлинение через закон Гука: ΔL=LN/EA

LN₁/EA= LN₂/EA= LN₃/EA, N₁=N₂=N₃ – получаем еще 3-е уравнение.