3.3. Напряженное состояние в точке. Закон парности касательных напряжений. Главные площадки и главные напряжения.

Напряженное состояние в данной точке тела характеризуется совокупностью нормальных и касательных напряжений на бесчисленном множестве различно ориентированных в пространстве площадок, которые можно провести через эту точку.

П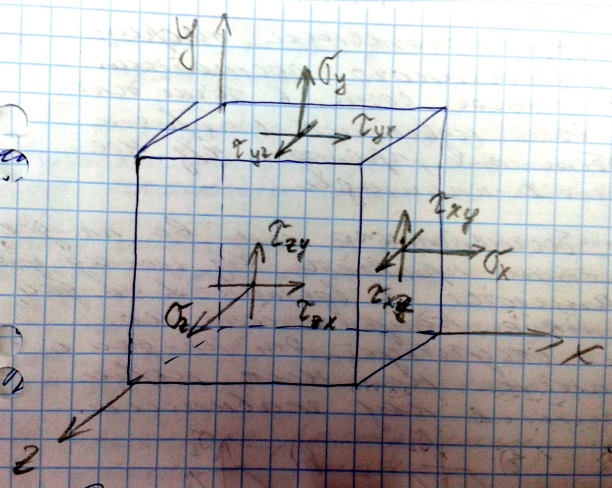 редполагаем, что в окрестности исследуемой точки выделен бесконечно малый элемент, имеющий форму прямоугольного параллелепипеда и напряжения, возникающего на его гранях извест. Рассмотри 3 взаимно перпендикулярные площадки:

Из условия равновесия выделенного элемента следует, что составляющая касательных напряжений, возникающих на любых 2-х взаимно перпендикулярных площадок, перпендикулярны общему ребру этих площадок, равны по абсолютному значению. ; ;

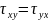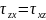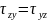
Это положение называется законом парности касательных напряжений. Следовательно, из 9 компонентов напряженного состояния в окрестности точки независимы лишь 6.

Первое положение теории напряженного состояния:

Н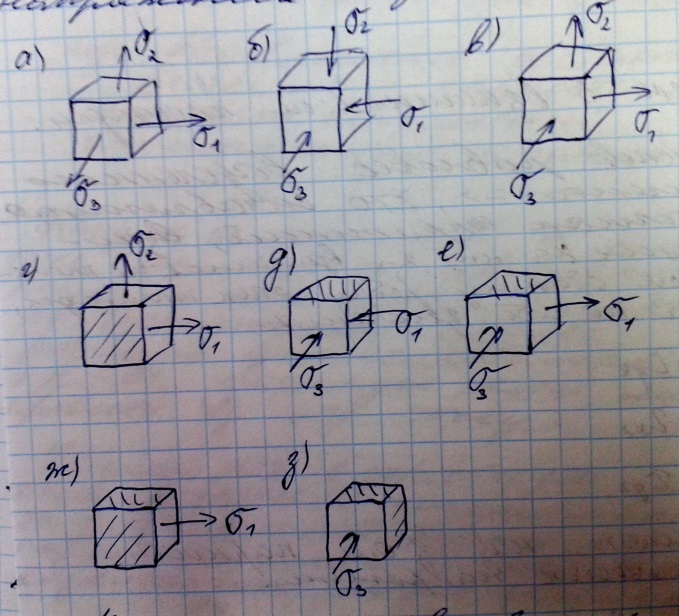 апряженное состояние в точке тела задано, если известны напряжения на любых 3-х, проходящих через нее взаимно перпендикулярных площадок. Среди бесчисленного множества площадок, которые можно провести через исследуемую точку, имеются 3 взаимно перпендикулярных площадки, касательное напряжение на которых отсутствует. Эти площадки и возникающее на них нормальное напряжение называются главными.

Классификацию видов напряженного состояния ведут по главному напряжению, если все 3 напряжения отличны от 0, напряженное состояние называется объединенным или пространственным, или трехосным.

В случае, если одно из главных напряжений = 0, напряженное состояние называется плоским или двухосным.

Если лишь одно из главных напряжений отлично от 0, напряженное состояние называет линейным или одноосным. Элементы, выделенные главными площадками для различных частных случаев напряженного состояния: а)трехосное растяжение б)трехосное сжатие в)трехосное смешанное напряженное состояние г)двухосное растяжение

д)двухосное сжатие е) двухосное смешанное напряженное состояние

ж)одноосное растяжение з)одноосное сжатие

Площадки, свободные от напряжения, называются нулевыми главными площадками (заштрихованы на рисунке).

3.4 Однородное растяжение бруса как пример реализации одноосного напряжения состояния мат-ла

П ри растяжении или сжатии прямого бруса в его поперечн сечен возникают только 1 внутр сіловой фактор - продольная сила N_z . прямые брусья, работающие на раст или сжат, - наз-ся стержнями. При растяжении N_z направлена от сечения и считается положительной(+), а при сжатии – к сечению и считается отриц. Для определения модуля и направления рассекают брус и для оставшейся части составл ур-ние равновесия: 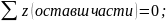N_z=-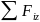

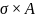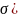Продольная сила поперечн сечен – равнодействующая внутр нормальных сил, возникшая в этом сечении. Nz= . если продол силы в разных сечениях не одинаковы, то строят эпюру – график изм-ния продол сил по длине бруса. Она нужна для расчета бруса на прочность. При раст или сжат возник только нормальные напряжения ( . В местах резкого изм формы или размеров бруса возникают местные напряжения – концентрация напряжений. Если норм напряжения по длине бруса не одинаковы, то строят эпюру.