8. Гипотеза де-Бройля. Опыты Дэвиссона и Джермера. Дифракция электро-нов, атомов и молекул. Корпускулярно-волновой дуализм. Особенности поведения микрообъектов.

Оказывается, и при этом мы вновь сошлемся на эксперимент, что и частицы вещества с ненулевой с массой (электроны, протоны, нейтроны, атомы, молекулы и т.д.) также обнаруживают волновые свойства, так что между ними и фото­нами нет принципиального различия.

В этом пункте при переходе от макро- к микрообъектам возникает известная трудность в понимании существа физических явлений. Действительно, на уровне макроявлений корпускулярное и волновое описание четко разграничены. На уровне микроявлений эта граница в значительной степени размывается и движение микрообъекта стано­вится одновременно и волновым, и корпускулярным.

Последовательной теорией, учитывающей эту особенность всех микрочастиц, является квантовая теория. Но прежде чем перейти к изложению ее основных идей, необходимо установить каким образом один и тот же физический объект в принципе может проявлять то корпускулярные, то волновые свойства и какая существует сопоставимость этих двух различных способов описания.

В оптических явлениях установлен критерий применимости понятия луча (т.е. корпускулярной картины) и найдены правила перехода от волновых понятий к корпускулярным. Продолжая рассуждения в этом направлении, можно надеяться! что здесь же лежит переход в обрат­ном направлении: от корпускулярных понятий классической механики к волновым представлениям квантовой механики.

Соответствующие идеи, использующие оптико-механическую анало­гию, были высказаны французским физиком Л. де Бройлем в 1924 г. Де Бройль выдвинул смелую гипотезу о том, что дуализм "волна-час­тица" не является особенностью одних только оптических явлений, но имеет универсальную применимость во всей физике микромира.

К допущению волновых свойств у материальных частиц его привели следующие соображения. В конце 20-х годов XIX в. В. Гамильтон обратил внимание на удивительную аналогию между геометри­ческой оптикой и классический (ньютоновской) механикой. Было пока­зано, что основные законы этих столь непохожих на первый взгляд разделов физики представимы в математически тождественной форме. В результате вместо того, чтобы рассматривать движение частицы во внешнем поле с потенциальной энергией 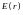, можно изучать распространение светового луча в оптически неоднородной среде с подобранным соответствующим образом показателем преломления . Эта эквивалентность описаний допускает и обратный переход.

Отмеченная аналогия распространялась Гамильтоном только на геометрическую оптику и классическую механику. Но, как уже отмеча­лось, геометрическая оптика является приближением более общей вол­новой оптики и не описывает сугубо волновых свойств света. В свою очередь, классическая механика также имеет ограниченную область применимости: она, как известно, не может объяснить существование дискретных уровней энергии в атомных системах.

Идея де Бройля заключалась в том, чтобы расширить аналогию между оптикой и механикой и волновой оптике сопоставить волновую механику, попытавшись применить последнюю к внутриатомным явлениям.

За открытие волновых свойств вещества Л. де Бройль в 1929 г. был удостоен Нобелевской премии.

Обратимся теперь к формальной стороне вопроса. Пусть мы имеем микрочастицу (например, электрон) с массой m, движущуюся в вакууме с постоянной скоростью 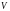. Пользуясь корпускулярным описанием, припишем частице энергию E и импульс 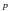в соответствии с формулами (рассмотрим общий случай релятивистской частицы).

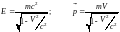. 11Equation Chapter 1.2 Section 1 (1.2.1)

С другой стороны, в волновой картине мы используем понятия частоты 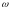и длины волны 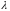(или волнового числа 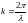). Если оба описания являются различными аспектами одного и того же физическо­го объекта, то между ними должна быть однозначная связь. Следуя де Бройлю, перенесем на случай частиц вещества те же правила пере­хода от одной картины к другой, справедливые в применении к све­ту:

(1.2.2)

Соотношения (1.2.2) получили название формул де Бройля. Длина волны, связанная с частицей, определяется выражением

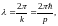(1.2.3)

ее называют длиной волны де Бройля. Нетрудно сообразить по аналогии со светом, что именно эта длина волны должна фигурировать в критериях применимости волновой или корпускулярной картин.

Наиболее простым типом волны в вакууме с определенной часто­той и волновым вектором 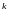является плоская монохроматическая волна

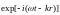
Поэтому в соответствии с формулами (1.2.2) свяжем с движением час­тицы волну вида

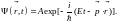(1.2.4)

Такую волну называют волной де Бройля. Непростой вопрос о физической природе этой волны и о толковании ее значений отложим на последующие параграфы.

Из определения (1.2.3) получим ряд полезных соотношений, свя­зывающих длину волны де Бройля с параметрами движущейся частицы. Подставив формулу (1.2.1) для импульса частицы p в (1.2.3), полу­чим зависимость от скорости частицы:

(1.2.5)

Выразив с помощью соотношения 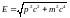импульс час­тицы p через ее полную энергию E, найдем, что

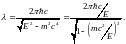(1.2.6)

Обозначим T кинетическую энергию частицы. Воспользовавшись определением , из (1.2.6) получим формулу

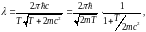(1.2.7)

выражающую дебройлевскую длину волны частицы через ее кинетичес­кую энергию.

В предельном случае нерелятивистской частицы, когда отноше­ние 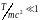, из (1.2.6) получим выражение для дебройлевской длины волны в нерелятивистском приближении:

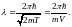(1.2.8)

Разумеется, выражение (1.2.8) можно было получить непосредственно из формулы (1.2.5) в пределе, когда отношение .

Опыт Дэвиссона — Джермера

Опыт Дэвиссона-Джермера — физический эксперимент по дифракции электронов.

Идея опыта

Проводилось исследование отражения электронов от монокристалла никеля. Установка включала в себя монокристалл никеля, сошлифованный под углом и установленный на держателе. На плоскость шлифа направлялся перпендикулярно пучок монохроматических электронов. Скорость электронов определялась напряжением на электронной пушке:

Под углом к падающему пучку электронов устанавливался цилиндр Фарадея, соединённый с чувствительным гальванометром. По показаниям гальванометра определялась интенсивность отражённого от кристалла электронного пучка. Вся установка находилась в вакууме.

В опытах измерялась интенсивность рассеянного кристаллом электронного пучка в зависимости от угла рассеяния от азимутального угла , от скорости электронов в пучке.

Опыты показали, что имеется ярко выраженная селективность (выборочность) рассеяния электронов. При различных значениях углов и скоростей, в отражённых лучах наблюдаются максимумы и минимумы интенсивности. Условие максимума:

Здесь — межплоскостное расстояние.

Т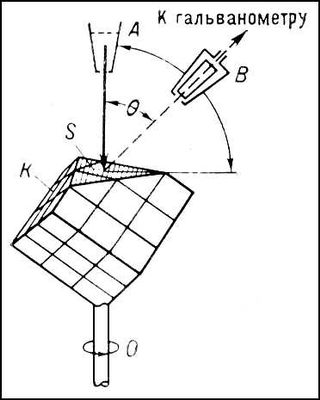 аким образом наблюдалась дифракция электронов на кристаллической решётке монокристала. Опыт явился блестящим подтверждением существования у микрочастиц волновых свойств.

Схема опыта Дэвиссона — Джермера: К — монокристалл никеля; А — источник электронов; В — приёмник электронов; q — угол отклонения электронных пучков. Пучок электронов падает перпендикулярно отшлифованной плоскости кристалла S. При поворотах кристалла вокруг оси О гальванометр, присоединённый к приёмнику В, даёт периодически возникающие максимумы

Корпускулярно-волновой дуализм – свойство любой микрочастицы обнаруживать признаки частицы (корпускулы) и волны. Наиболее ярко корпускулярно-волновой дуализм проявляется у элементарных частиц. Электрон, нейтрон, фотон в одних условиях ведут себя как хорошо локализованные в пространстве материальные объекты (частицы), двигающиеся с определёнными энергиями и импульсами по классическим траекториям, а в других – как волны, что проявляется в их способности к интерференции и дифракции. Так электромагнитная волна, рассеиваясь на свободных электронах, ведёт себя как поток отдельных частиц – фотонов, являющихся квантами электромагнитного поля (Комптона эффект), причём импульс фотона даётся формулой р = h/λ, где λ – длина электромагнитной волны, а h – постоянная Планка. Эта формула сама по себе – свидетельство дуализма. В ней слева – импульс отдельной частицы (фотона), а справа – длина волны фотона.

Дуализм электронов, которые мы привыкли считать частицами, проявляется в том, что при отражении от поверхности монокристалла наблюдается дифракционная картина, что является проявлением волновых свойств электронов. Количественная связь между корпускулярными и волновыми характеристиками электрона та же, что и для фотона: р = h/λ (р – импульс электрона, а λ – его длина волны де Бройля). Корпускулярно-волновой дуализм лежит в основе квантовой физики.