8.5. Характеристики качества систем на основе н-теории

Известна оценка качества на основе передаточной функции по ошибке , для системы (рис. 8.9).

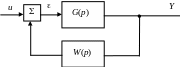
Рис. 8.9. Структурная схема системы автоматического регулирования

Передаточную функцию по ошибке называют также функцией чувствительности и обозначают

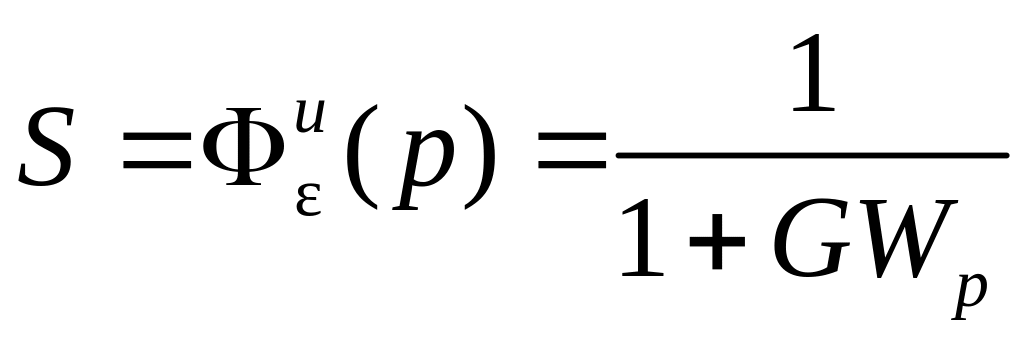. (8.52)

Она соответствует ранее рассмотренному соотношению

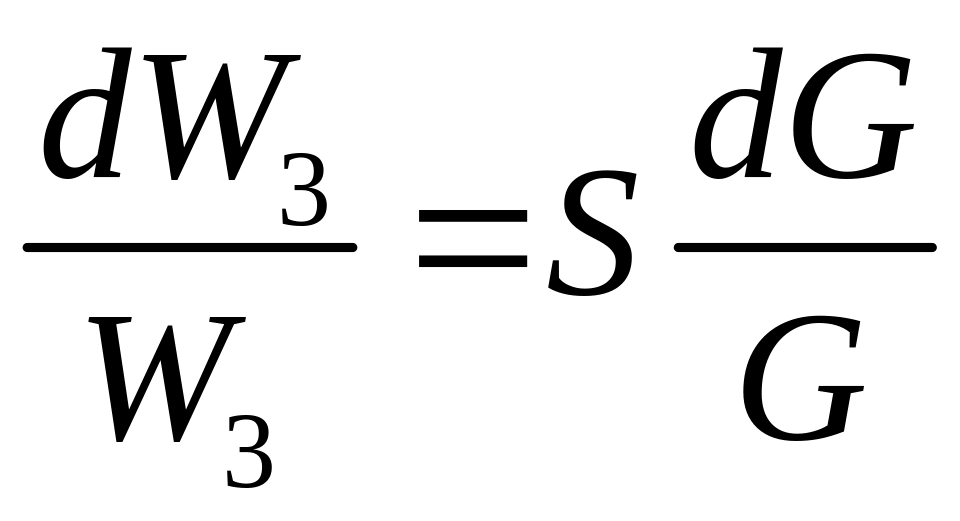, (8.53)

где W₃  передаточная функция замкнутой системы; dW, dG  изменения, соответственно, передаточной функции системы и объекта.

Н^-теория использует передаточную функцию замкнутой системы от входа до выхода регулятора:

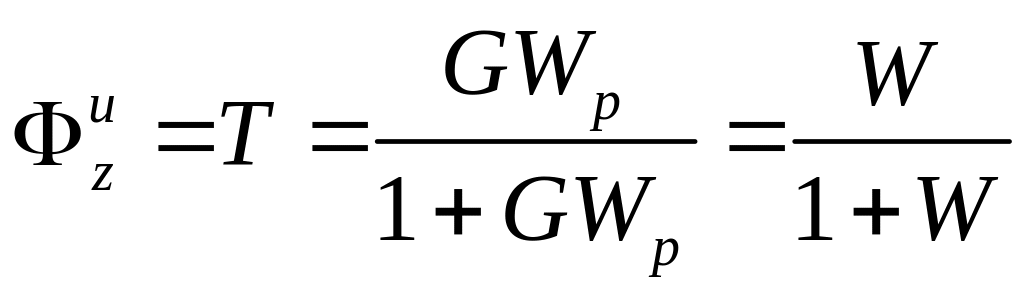, (8.54)

где W  передаточная функция разомкнутой системы, называемая функцией дополнительной чувствительности. Сумма приведенных чувствительностей равна

S + T = 1. (8.55)

Введем некоторую функцию ₁(p), которая будет формировать вес функций чувствительности. Норму функций ₁(p)S(p) в пространстве Н^ обозначим

||₁(p)S(p)||_.

Считается, что система обладает хорошим качеством, если

||, S||  1. (8.56)

Пусть на вход систем (рис. 8.9) поступает сигнал U(t) сформированный из гармоник U₁(t) единичной амплитуды и нулевой фазы. Тогда составим структурную схему (рис. 8.10).

Рис. 8.10. Структурная схема математического выражения

При входном сигнале определенной частоты можно записать

, (8.57)

где |₁(j)||S(j)| есть амплитуда |_уст.(t)|. В силу определения Н^-нормы (8.4) имеем

||₁S||_ = sup|₁(j)||S (j)| = sup |_уст.(t)| (8.58)

и выполнения условия (8.56) можно заключить, что амплитуда установившейся ошибки системы не превысит значения единицы при самом неблагоприятном сигнале из класса входных сигналов (₁). Это свойство характеризует поведение системы по отношению к классу воздействий. Если V₁(t) есть белый шум единичной интенсивности, тогда спектральная плотность ошибки (t) системы будет

. (8.59)

Откуда с учетом условия (8.56) можно утверждать, что средняя мощность сигнала ошибки при обработке системой случайных сигналов со спектральной плотностью |₁(j)|² будет меньше единицы при самом неблагоприятном частотном диапазоне спектра.

С учетом свойств Н^-пространства можно отметить, что (8.56) означает

,

или . (8.60)

Если годограф 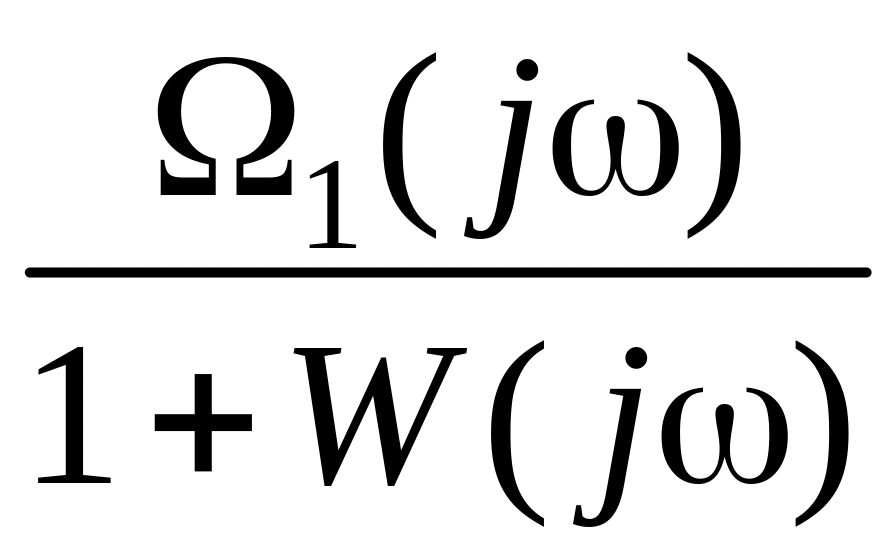целиком лежит внутри окружности единичного радиуса, проведенной из точки (1, j0), то условие (8.60) выполняется.

Условие (8.60) можно приближенно представить в виде

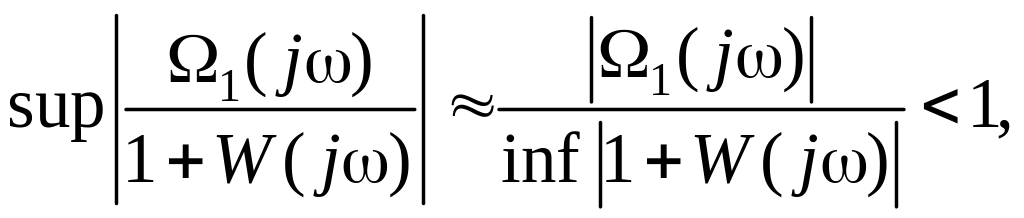
или |₁(j)| < inf |1 + W(j)|. (8.61)

На основании условия (8.61) комплексная частотная характеристика W(j) должна лежать вне окружности радиуса |₁(j)|, проведенной из точки (1, j0). Здесь важно учесть спектр реальных входных сигналов ₁(j).

Если выполнять оценку с помощью функции S, то критерий качества

||S||^ < 1 (8.62)

соответствует

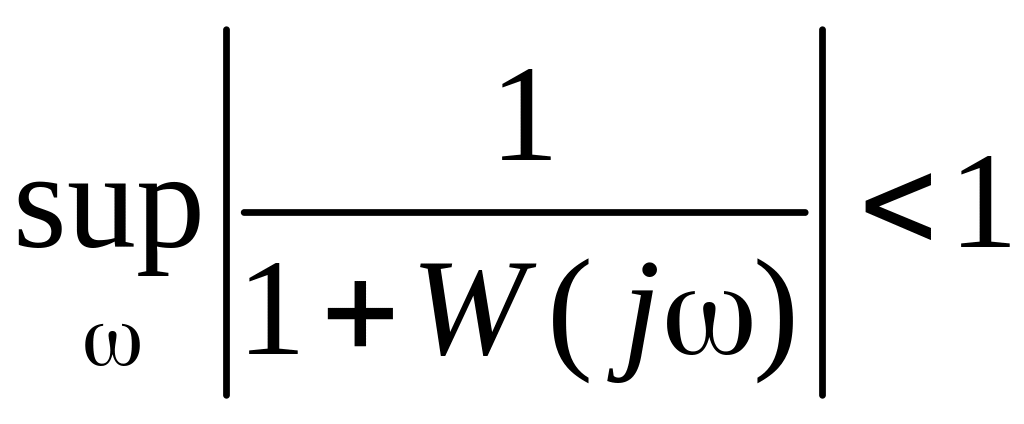, (8.63)

откуда имеем

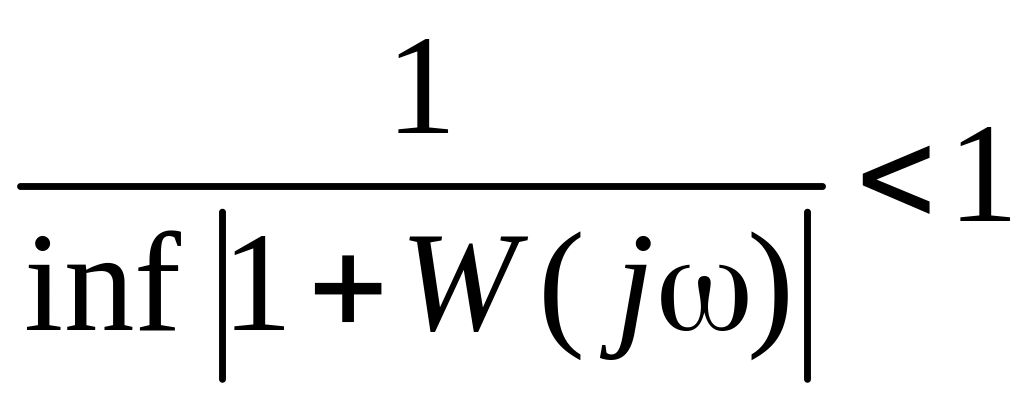, (8.64)

или

. (8.65)

Условие (8.65) означает, что кривая W(j) не должна входить в круг радиуса 1, с центром в точке (1, j0).

Если выполнять оценку качества системы на основе нормы функции Т, то имеем

||T||^ < 1 (8.66)

и соответственно

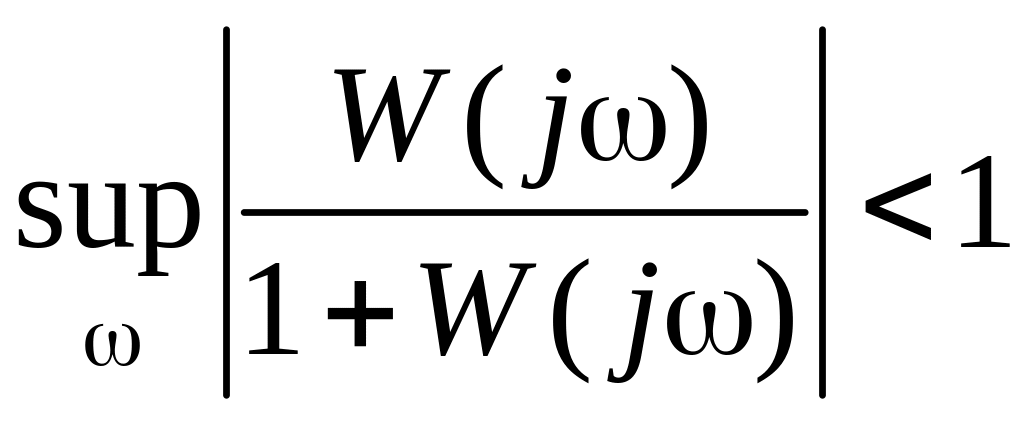, (8.67)

или приближенно

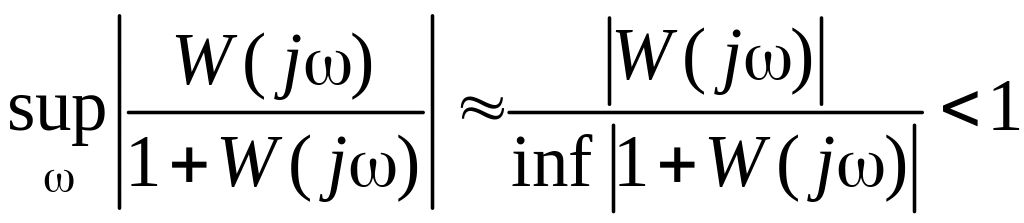, (8.68)

откуда запишем условие

, (8.69)

где ₁  частота, на которой обеспечивается инфинимум |1 + W(j)|.

Условие (8.69) означает, что кривая W(j) не должна входить в круг радиуса |W(j₁)|, поскольку, как правило, |W(j₁)| существенно меньше единицы, условие (8.69) менее жесткое, чем условие (8.62).

Использование критерия

||₂T||_ < 1 (8.70)

при соответствующем векторе весовой функции ₂ позволяет смягчить условие (8.69).

Задача Нехари

Пусть нужно найти устойчивую матрицу Х(р), которая в Н^-пространстве аппроксимирует неустойчивую матрицу R, так чтобы ошибка RX была минимальной в смысле Н^-нормы . Оптимальное значение Х представляет оператор Теплица _R, а (RX_опт) есть оператор Ганкеля.