Глава 8. Анализ и синтез систем
автоматического управления в условиях
неопределенности
8.1. Элементы Н-теории
Множество всех дробно-рациональных функций комплексного аргумента p = c + j типа
B(p)/A(p) (8.1)
являются полем пространства. Множество всех полиномов комплексного полинома с вещественными коэффициентами
,
(8.2)
принадлежат к полю, которое обозначается символом R(p).
Если бы эти коэффициенты были комплексными, то такое поле обозначают символом С(р).
Поле это алгебраическое понятие, связанное с алгебраическими операциями над множеством элементов определенного признака. В результате операций над элементами этих множеств получаем элементы, которые принадлежат к этому полю. Наряду с полями бывают множества целых чисел, которые по аналогичным свойствам объединяются в свое пространство, называемое кольцом и обозначаемое часто символом Z.
Среди свойств пространств можно выделить, например, свойства аддитивности (коммутативность, ассоциативность, существование противоположного элемента и нуля) и свойство однородности (операции умножение на число). Если пространство обладает указанными свойствами, то оно относится к классу линейных.
Если среди операций в линейном пространстве существует операция, переводящая элементы множества V в элементы множества неотрицательных действительных чисел и позволяющая найти норму, то такое пространство называется нормированным.
Во всяком нормированном пространстве можно ввести меру удаленности элементов этого пространства метрику. Если оказывается, что всякая сходящаяся последовательность точек пространства содержит и предельную точку с предельными свойствами, то такое метрическое пространство называют полным. Полное нормированное пространство называют банаховым. Если в линейном пространстве вводится понятие скалярного произведения элементов (х, у), то такое пространство называется евклидовым пространством Е и нормированным с нормой
. (8.3)
Полное евклидово пространство бесконечного числа измерений называется гильбертовым пространством Н.
Элементами нормированных пространств могут быть и функции, функционалы и операторы. Нормы каждого из этих математических объектов задаются по-разному. Так, Лебегом были сформулированы менее жесткие требования для интегрируемости функции, чем Риманом, что позволяет охватить более широкий класс функций, которые можно назвать элементами пространства L.
Пространство Н включает функции, свойствами которых обладают большинство функций, используемых в теории управления. Пространство Н включает правильные дробно-рациональные функции, не содержащие особенностей в правой полуплоскости и на мнимой оси комплексного переменного.
Функция, комплексной переменной F(p), принадлежащая пространству Н имеет норму
. (8.4)
Для линейной системы с передаточной функцией
,
(8.5)
где W комплексно-сопряженная функции W(j).
Норма ||W(j)|| соответствует пику амплитудно-частотной характеристики. Частота, которая удовлетворяет этому условию, определяется на основе
(8.6)
или для матричной передаточной функции
. (8.7)
Если исходной матричной передаточной функции в пространстве состояния соответствует выражение
WT(p) = C[pI – A]1B, (8.8)
то можно определить матрицу Гамильтона:
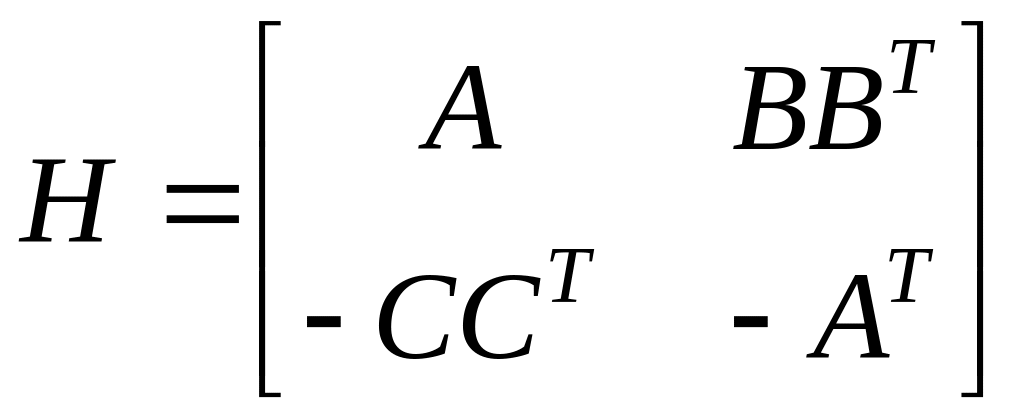. (8.9)
Если матрица Гамильтона не имеет собственных чисел на мнимой оси, то существует теорема, утверждающая что ||WT|| < 1.
На основе этой теоремы строится алгоритм поиска ||WT||. Фактически ищется не сама норма, а ее верхняя оценка. Для этого масштабируют WT, используя положительное число такое, чтобы выполнялось условие ||1G|| < 1, эквивалентное ||G|| < . Можно взять, например, вместо В матрицу В1. Тогда изменится матрица Гамильтона. Для выбранного ищут собственные значения и оценивают на близость к мнимой оси с заданной точностью.
8.2. Особенности описания систем в н-теории
Пусть многомерная система управления имеет структурную схему (рис. 8.1).
Рис. 8.1. Структурная схема линейной многомерной системы
Модель системы управления имеет вид
O(p) = G(p)J(p). (8.10)
Вектор J(p) включает вектор возмущающих (р) и управляющих u(p) воздействий.
Через Z(p) обозначены выходы для контроля качества системы. Через у(р) обозначены выходы, используемые для улучшения качества систем с помощью регулятора.
Можно выделить составляющие модели типа
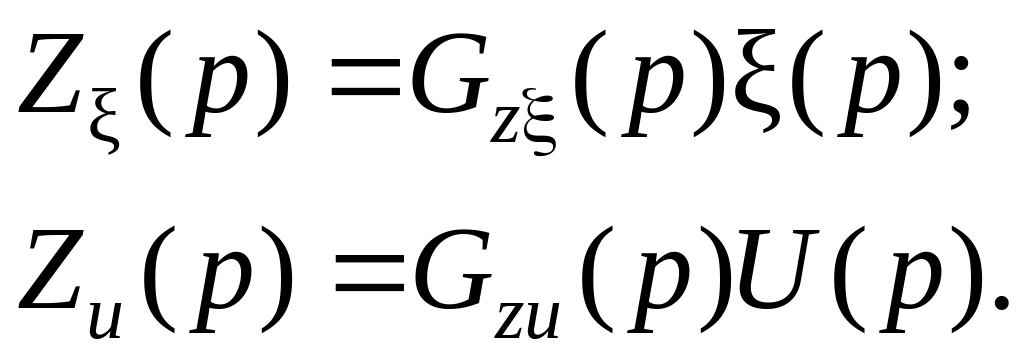(8.11)
Таким образом, при представлении сигналов и операторов в области преобразований Лапласа модель системы не имеет отличий от ранее использованных моделей.
В пространстве состояний соотношение (8.10) традиционно представляется выражениями
(8.12)
В Н-теории управления распространена другая форма записи (8.12) в виде (8.10), но во временной форме
,
(8.13)
где
,
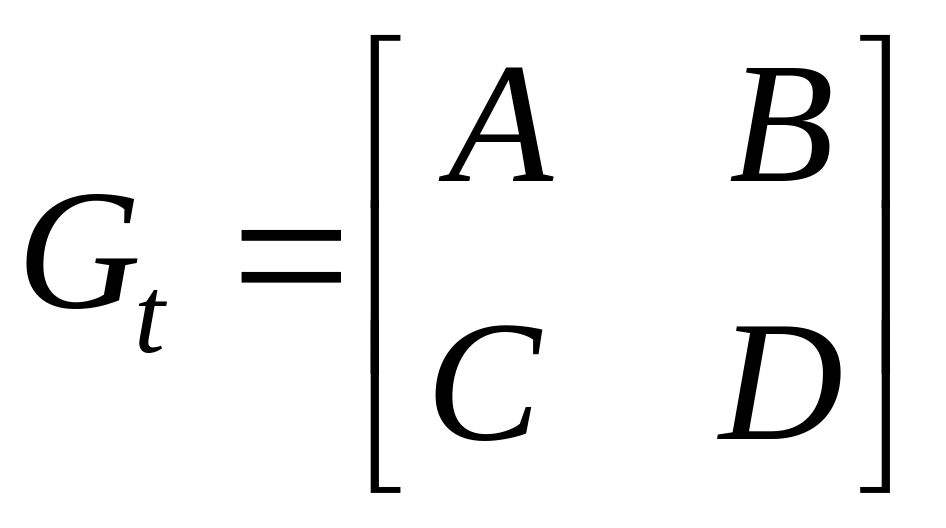O0
и J0
обобщенные векторы соответственно
выхода и входа.
При большей детализации модели (8.12) относительно переменных структурной схемы рис. 8.1 можем записать
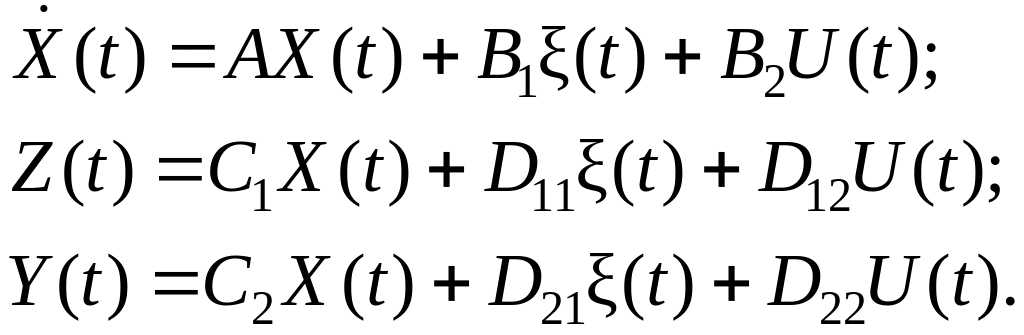(8.14)
Матрицу Gt для системы в виде уравнений (8.14) можно записать
,
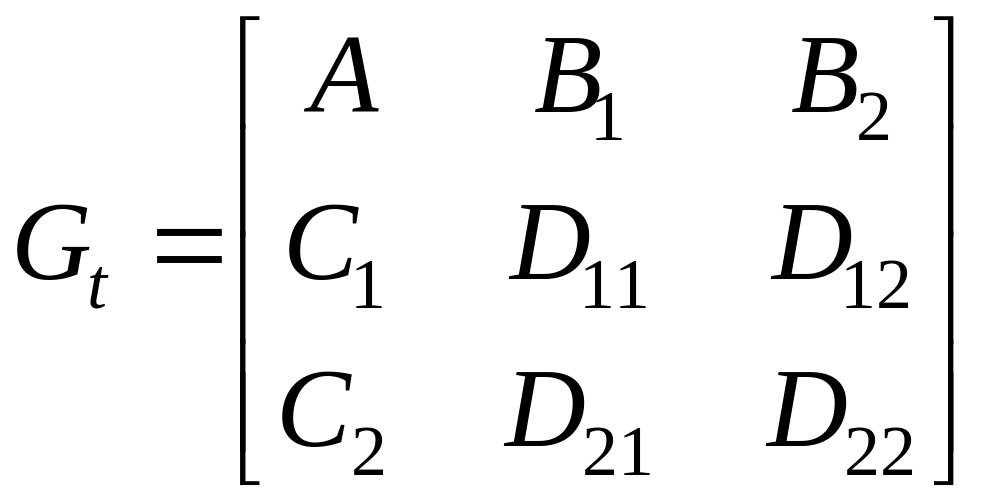(8.15)
где сплошные и пунктирные линии используются только для наглядности и в дальнейшем будут опущены.
Используя правила структурных преобразований линейных многомерных систем, введем понятие линейных дробных преобразований.
Рассмотрим структурную схему системы (рис. 8.2).
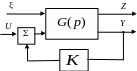
Рис. 8.2. Структурная схема системы с регулятором
Передаточная функция системы по каналу z равна
.
(8.16)
Близкое к виду (8.10) запишем уравнение
FL(G, K) = G11 + G12K(I + G22K)1G21, (8.17)
которое называют нижним линейным дробным преобразованием.
Структурная схема системы управления приведена на рис. 8.3.
Рис.8.3. Структурная схема системы управления
По аналогии с выражением (8.17) можно записать верхнее линейное дробное преобразование
Fu(G, ) = G22 + G21(I + G11K)1G12, (8.18)
которое близко к
передаточной функции системы (рис. 8.2)
по каналу
U(p)
Y(p).
Если существуют обратные матрицы K1,
1,
то в результате преобразований FL(G,
K)
совпадает с
и Fu(G,
)
совпадает
с
.
Выполним преобразование FL(G, K):
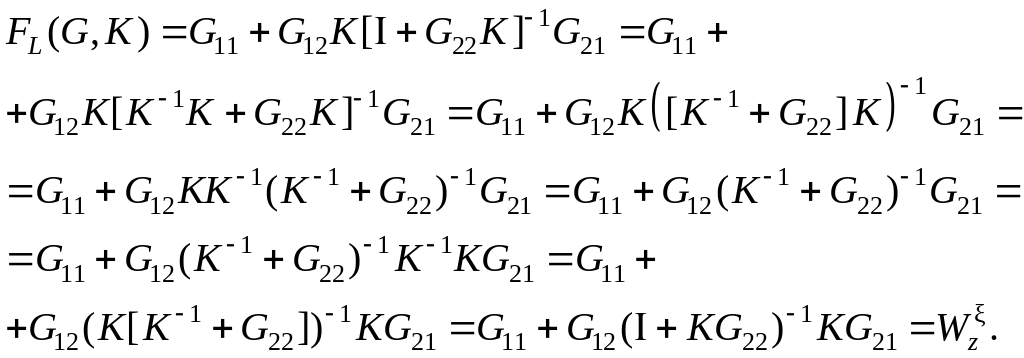(8.19)
Реальная работа системы проходит в условиях неопределенности за счет внешних воздействий, возмущений конкретных параметров системы (структурированные возмущения) и в виде возмущения матричной передаточной функции (неструктурированные возмущения).
Рассмотрим основные способы задания неструктурированных возмущений. Возмущающая добавка (р) является аддитивной
G(p) + (p) = Ga(p), (8.20)
а структура системы имеет вид (рис. 8.4).
Рис. 8.4. Структурная схема аддитивной неопределенности объекта
Неструктурированные возмущения могут быть в виде мульти-пликативной добавки
.
(8.21)
Структура системы имеет вид (рис. 8.5)
Рис. 8.5. Структурная схема мультипликативной неопределенности объекта
Также можно представить неопределенности в виде аддитивных взаимно простых добавок
,
(8.22)
составляющих схему (рис. 8.6).
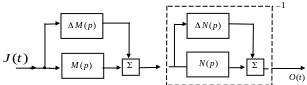
Рис. 8.6. Структурная схема с неопределенностью в виде компонент
с взаимнообратной связью
Все рассмотренные неструктурированные возмущения можно описать с помощью верхних линейных дробных преобразований.
Введем вместо G(p) новую передаточную матрицу обобщенного объекта следующего вида:
для Ga
;
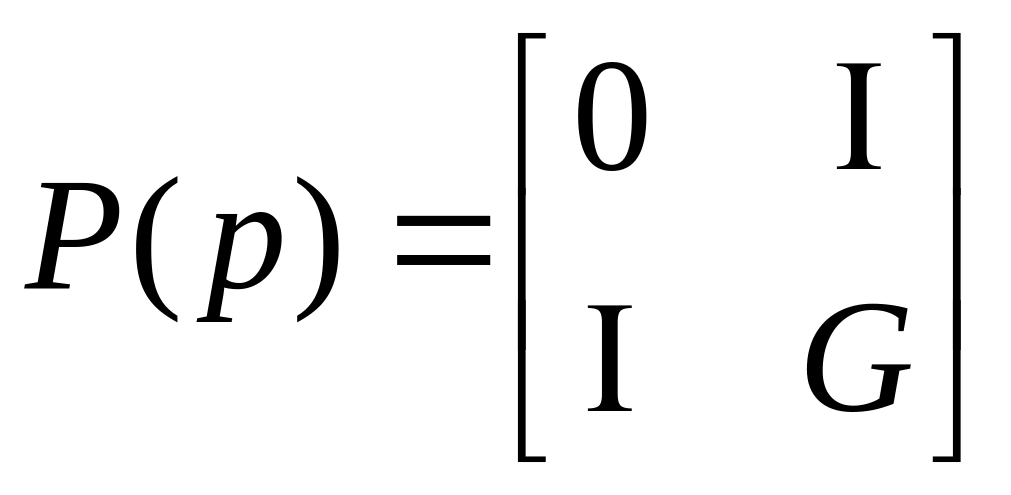для GM
;
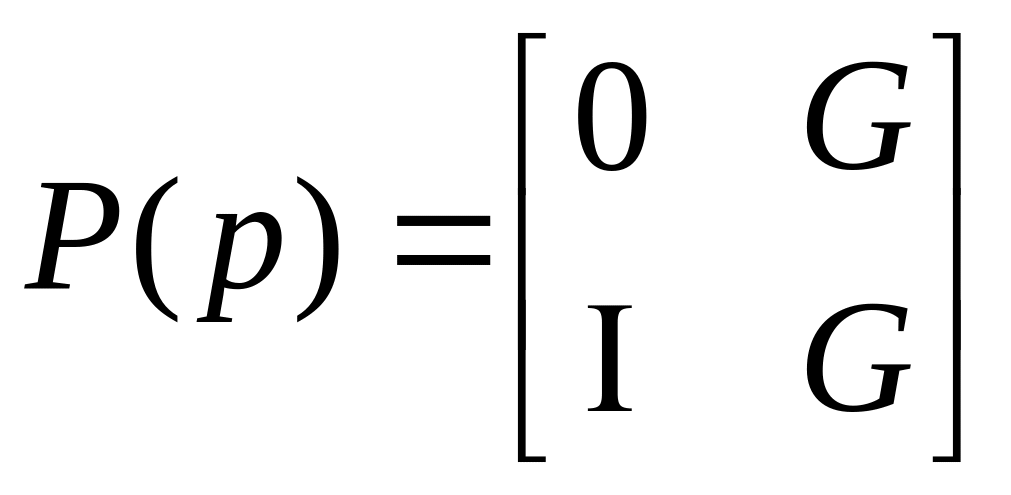для Ga
.
Запишем Fu(p, ) согласно (8.18), например, для GM:
.
С учетом схем рис. 8.2, рис. 8.5 можно представить структуру данной системы с неопределенностью объекта в виде рис. 8.7.
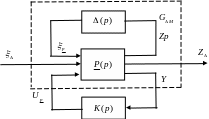
Рис. 8.7. Структурная схема системы с неопределенностью объекта (р)
Блоки обобщенной передаточной матрицы объекта GM на основании (8.21) равны
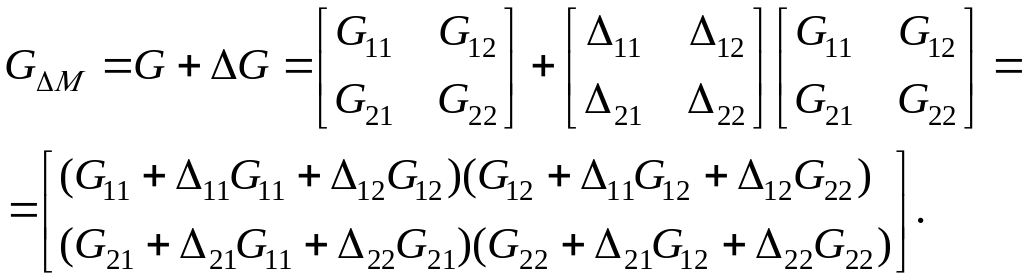(8.23)
Используя приведенное
выражение и формулу (8.22),
можно найти передаточную матричную
функцию
:
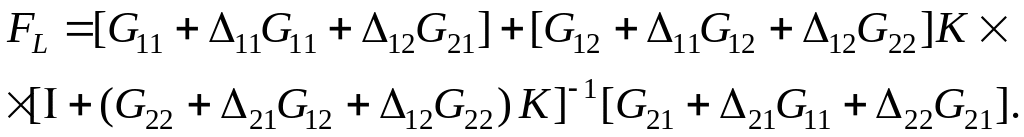(8.24)