6.7. Оптимальное управление системами с распределенными параметрами

Для решения задачи воспользуемся принципом максимума. Ограничимся случаем параболического уравнения второго порядка в нормированном виде относительно пространственной координаты z

(6.145)

с граничными условиями:

; (6.146)

. (6.147)

В качестве критерия качества используем форму, записанную в виде:

(6.148)

где r, s  пространственные координаты по оси z.

Функции Гамильтона составляются в виде

(6.149)

; (6.150)

; (6.151)

. (6.152)

Необходимые условия оптимальности имеют вид

(6.153)

; (6.154)

. (6.155)

Если уравнение зависит только от времени u(t), то необходимые условия изменяются и имеют вид

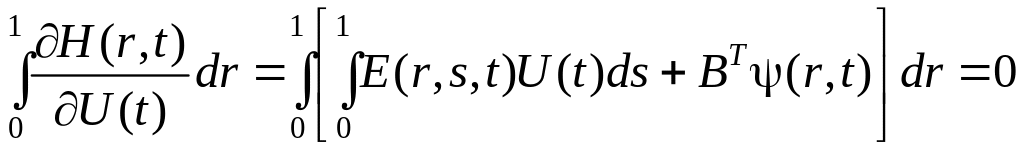. (6.156)

Из условия (6.153) имеем

(6.157)

где .

Подставляя (6.157) в (6.156), получим

. (6.158)

Таким же образом получим зависимости для U₀(t) и U₁(t):

; (6.159)

. (6.160)

Уравнения для сопряженных переменных  имеют вид

(6.161)

с граничными условиями:

, (6.162)

(6.163)

Введем матрицу S(r, s, t) в виде уравнения

. (6.164)

Производная по времени выражения (6.164) имеет вид

или

. (6.165)

С учетом (6.164) перепишем правую часть выражения (6.161):

. (6.166)

Можно преобразовать часть составляющих в уравнениях (6.165, 6.166) к виду

(6.167)

. (6.168)

В результате преобразований сопряженные переменные запишем

(6.169)

В свою очередь можно переписать часть составляющих (6.169) в виде

(6.170)

; (6.171)

. (6.172)

Подставляя (6.167)–(6.172) в (6.165), (6.166), получаем уравнение

(6.173)

с граничными условиями

; (6.174)

(6.175)

и условием на конечное состояние

. (6.176)

Тогда перепишем оптимальный закон управления

(6.177)

и для u(t)

. (6.178)

Граничные условия задаются в виде

; (6.179)

. (6.180)

На основании уравнений (6.173)(6.176) можно находить S(r, s, t) и затем использовать в уравнениях (6.177)(6.180).

В качестве примера рассмотрим теплообменник с паровой рубашкой. Вдоль теплообменника длиной L установлены датчики температуры в точках . Управление осуществляется изменением положения клапана, регулирующего подачу пара. Модель процесса имеет вид

,

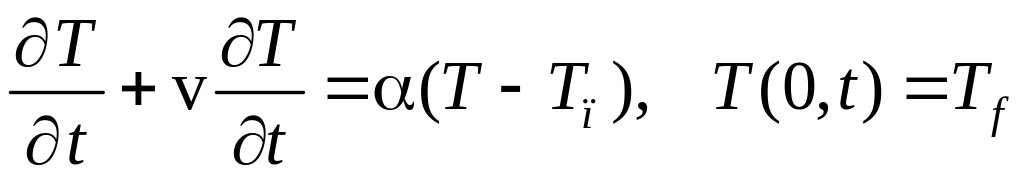где Т  температура нагреваемой жидкости, Т_п  температура паровой рубашки; v  скорость жидкости;  - коэффициент теплообмена.

Введем новые координаты:

х = Т – Т_д, u = Т_п – Т_пд ,

где Т_д  заданное распределение температуры вдоль теплообменника, Т_пд  распределение температуры паровой рубашки. В новых переменных модель имеет вид

.

Критерий качества примем в виде

.

Отметим, что приведенным формулам в данной задаче соответствует

Оптимальный закон регулирования на основе (6.178) равен

;
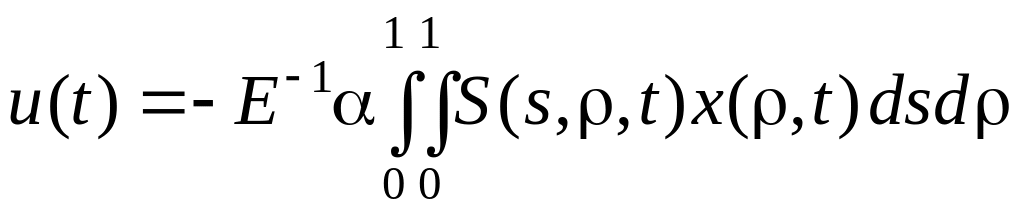