6.3.1. Свойства функции Гамильтона на оптимальном решении
Функция Гамильтона зависит от переменных x, , t и управления и, которое может иметь разрывы первого рода. Однако функция Гамильтона остается непрерывной по t.
Вычислим полную производную функции Н по времени:
.
Поскольку
,
производная
для оптимального закона внутри допустимого
диапазона изменения и,
а на границе
,
то
.
Функция Гамильтона на оптимальном решении не меняется.
Для задачи о максимальном быстродействии линейного объекта
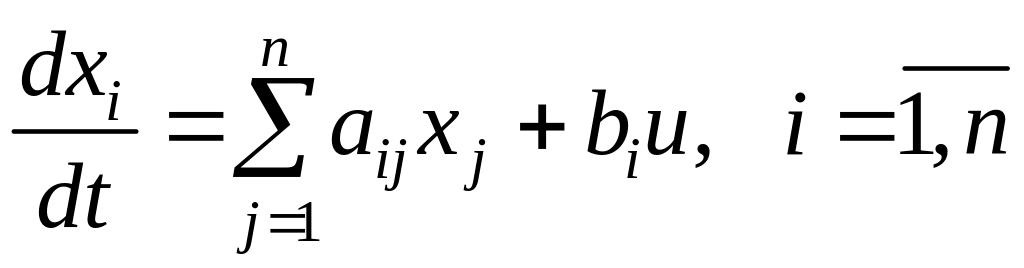(6.39)
рассмотрим вариант модели, когда характеристическое уравнение (при и = 0) имеет только отрицательные действительные корни. Сопряженные уравнения в этом случае можно переписать в виде
.
(6.40)
Известно
;
(6.41)
;
(6.42)
;
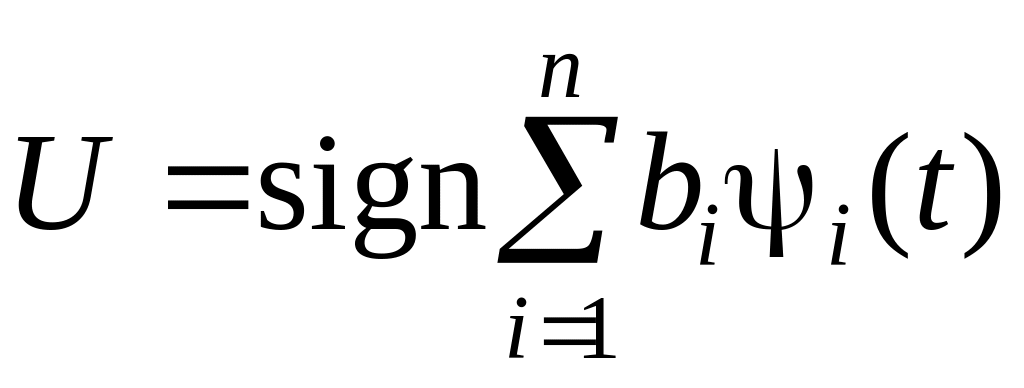(6.43)
(6.44)
где
.
Выражение
переходит через нуль не более чем (n
– 1) раз и имеет, следовательно, не более
n
интервалов постоянства знака. Отсюда,
как следствие, управляющее воздействие
и
имеет в общем случае n
интервалов постоянства знака для систем
n-го
порядка.
6.4. Динамическое программирование
Метод динамического программирования был предложен американским ученым Р. Беллманом примерно в те же годы, что и принцип максимума.
Р. Беллман интересовался решением задач путем разложения сложной на отдельные простейшие, причем каждое из составных решений связано с общим решением.
В основу динамического программирования положен принцип, получивший наименование принципа оптимальности. Согласно этому принципу оптимальное уравнение определяется конечной целью управления и состоянием системы в рассматриваемый момент времени, независимо от того, каким образом система пришла в это состояние. Для любой оптимальной траектории каждый ее участок, связывающий любую промежуточную точку этой траектории с конечной, также является оптимальной траекторией.
Пусть имеем дискретную модель объекта
x(k+1) = f(x(k),u(k)) (6.45)
и необходимо найти
управляющие воздействия
,
которые обеспечат минимум критерия:
. (6.46)
Критерий оптимальности является функцией (n+1) переменных U(k), каждая из которых действует на своем временном интервале, что позволяет задачу расчленить на n-подзадач, связанных на соседних временных интервалах. В результате имеем последовательную цепочку простых задач, каждая из которых требует найти лишь одно управляющее воздействие для фиксированного интервала времени. При таком подходе участки процесса рассматриваются в последовательности обратной их номеру от конца процесса к его началу.
Пусть структура процесса в виде отдельных участков имеет вид рис. 6.5.
Рис. 6.5. Структура дискретного процесса управления
Для последнего интервала времени из допустимого диапазона u(n – 1) U при возможных значениях x(n – 1) X можно выбрать такие u(n – 1), которые минимизируют величину Jn.
Обозначим минимальное значение Jn через n (x(n – 1)):
.
(6.47)
Затем переходим к предпоследнему интервалу времени n 1. Значения входной координаты и управляющего воздействия здесь соответственно равны x(n 2) и u(n 2). Теперь минимизацию Jn-1 будем осуществлять с помощью управления u(n 2), дополняя полученные решения результатами n для последнего участка, вводя обозначения
или
переписав с учетом модели движения
объекта
Расчеты, производимые аналогичным образом для произвольного интервала времени, можно записать в виде рекуррентной формулы:
(6.48)
Так продолжается расчет до тех пор, пока не приходим к первому интервалу с заданным значением х(0), что позволяет, используя модель динамики движения объекта для каждого такта, находить из ранее зафиксированных табличных значений оптимальные значения (Uопт(0), Uопт(1), Uопт(2), …).
Этот метод можно рассматривать как алгоритм для вычисления на ПЭВМ. Используем теперь идею динамического программирования для оптимизации управления в непрерывных процессах.
Пусть требуется выбрать x(t) таким образом, чтобы интеграл
(6.49)
принял минимальное значение при движении из точки x(t0) в точку x(tf). Пусть (x, t) есть функция, соответствующая минимуму интеграла J с нижним пределом t:
. (6.50)
Минимизацию можно производить, например, по :
. (6.51)
Для использования ранее рассмотренного принципа оптимальности разобьем траекторию движения системы на два интервала времени [t, t + ] и [t + , tf]. Первый интервал времени выбираем малым. Для него начальным условием является x(t), а для второго x(t + ).
Перепишем функцию (x, t) в виде
.
(6.52)
Воспользовавшись принципом оптимальности, можем считать, что для интервала [t + , tf] существует оптимальное решение. Это позволяет записать
, (6.53)
где
.
Так как очень мало, то можно переписать (6.53) в виде
.
Разложим в ряд Тейлора выражение
и ограничимся линейными членами разложения. Тогда можно записать (x, t) следующим образом:
.
(6.54)
Выражение (6.54) можно привести к виду
.
(6.55)
Окончательно запишем уравнение в виде
. (6.56)
Если бы х был вектором, тогда уравнение (6.56) записывалось бы в виде
. (6.57)
Назовем полученное уравнение уравнением Беллмана для непрерывных систем.
Рассмотрим пример управления объектом первого порядка:
где
Пусть критерий качества системы имеет вид
.
Введем функцию
.
Используя уравнение Беллмана, запишем
.
Функция в фигурных скобках достигает минимум при условии
.
Оптимальное управляющее воздействие принимает значения +U или U в соответствии со знаком производной /x, удовлетворяющей дифференциальному уравнению в частных производных:
.
Аналитическое решение этой задачи трудно получить и поэтому часто используют численные методы. Как и в случае с принципом максимума, так и в случае использования динамического программирования, мы имеем проблему с нахождением функции (t).