6.12. Метод последовательных приближений для решения задачи синтеза оптимальных управлений

Пусть задана система

, (6.275)

причем фазовые координаты х₁, …, х_n и управления u₁,…,u_n подчинены ограничениям вида

(6.276)

и задан функционал

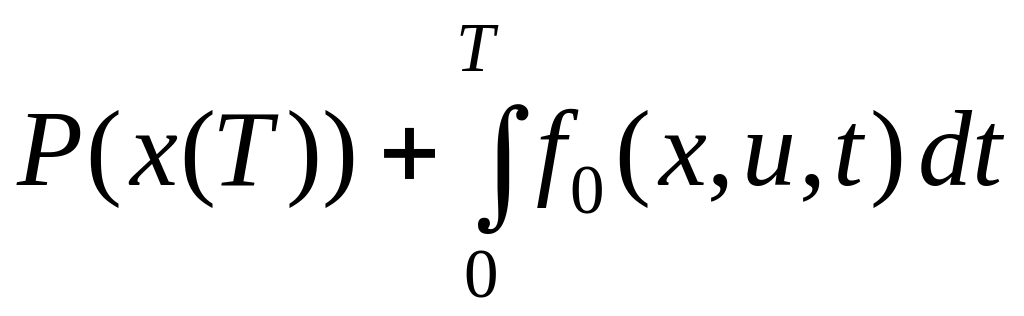, (6.277)

где Т > 0  фиксированный момент времени. Возьмем управление u(x, t). Подставим его в (6.275) и построим решение полученной системы:

, (6.278)

где х₁  некоторая точка фазового пространства. Вычислим значение функционала (6.276) при управлении u = u(x, t). Тогда получим некоторую величину J(u, x₁). Управление u₀ (x, t) называется оптимальным, если оно доставляет величине J(u, x₁) возможное наименьшее значение в каждой точке х₁ и притом удовлетворяет ограничениям (6.276).

Рассмотрим метод последовательных приближений для отыскания оптимального управления u₀ (x, t). Пусть u₁ (x, t)  некоторое допустимое управление. Подставив это управление в систему (1), найдем решение получившихся уравнений x = x(t, x₁). Далее рассмотрим уравнение

, (6.279)

где V₁ – искомая функция.

Величина х в правой части уравнения (6.279) есть решение x(t, x₁) упомянутой системы. Найдем решение уравнения (6.279) с начальным условием

при t = T. (6.280)

В результате получим функцию . Пользуясь решением системы, исключим вектор х₁ из функции . Тогда получим функцию V₁(x, t). Величина

Z = V₁ – V(x, t)

является интегралом системы

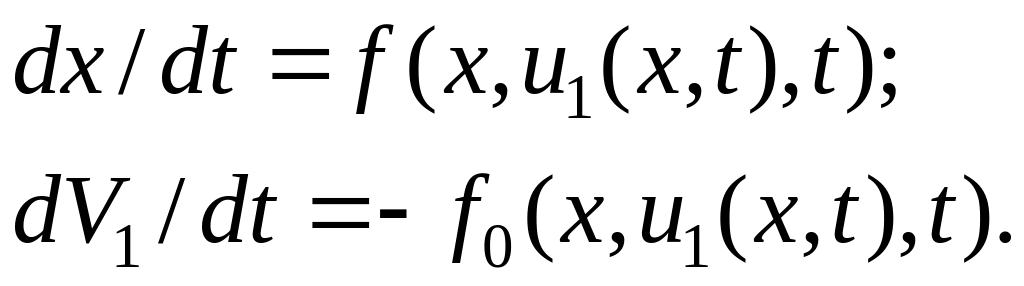(6.281)

При этом интеграл принимает нулевое значение на любом движении вида x = x(t, x₁), . Пользуясь функцией V₁, построим управление u₂ (x, t) так, чтобы оно удовлетворяло ограничению (6.276) и доставляло функции

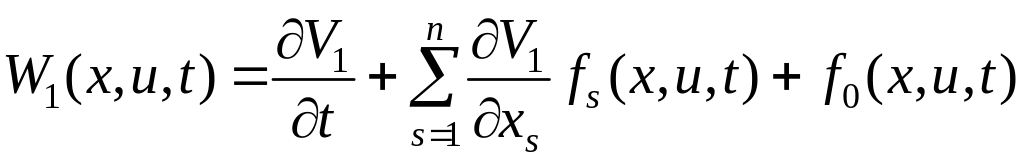
возможное наименьшее значение. Разумеется, что возможное наименьшее значение функции W₁ (x, u₁(x, t), t) не положительно, так как W₁ (x, u₁(x, t), t)  0.

С функцией u₂ (x, t) поступим точно так же, как и с u₁ (x, t). В результате этого получаются последовательности u₁, u₂, …, V₁ (x, t), V₂ (x, t) … .

Если процесс построения этих последовательностей оказывается возможным, то для любой точки х₁ последовательность u₁, u₂, … будет минимизирующей:

,

так что

В общем случае этот метод остается методом минимизации функционала и сходимость его к оптимальному управлению имеет место, вообще говоря, лишь при выполнении ограничительных условий на правые части системы (6.275), на функции g_j, входящие в (6.276), и на Р и f₀ из (6.277). Построение последовательных приближений для систем с неограниченным временем еще более затруднительно. Действительно, пусть дан функционал

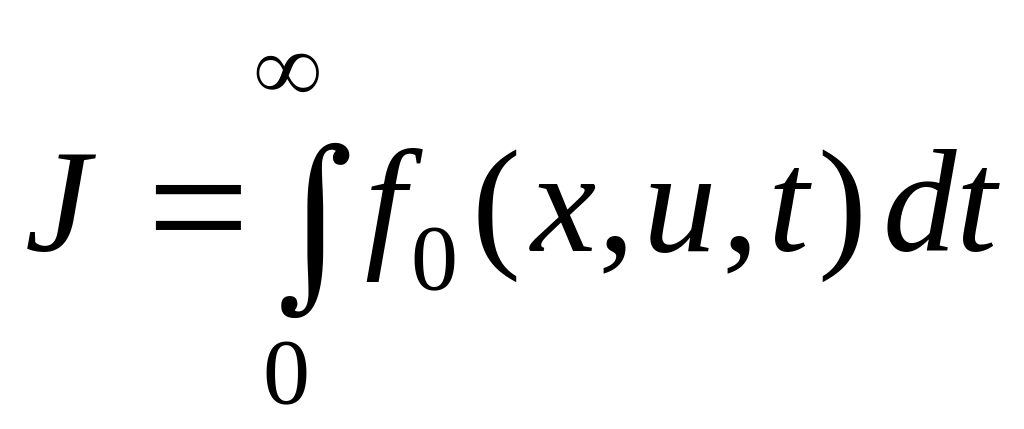. (6.282)

Допустимыми управлениями u (x, t) будем считать такие, при которых система (6.275) имеет асимптотически устойчивое нулевое решение, и выполняются условия (6.276). Пусть u₁ (x, t)  некоторое допустимое управление. Построим семейство решений х = х (t, х₁) и функцию

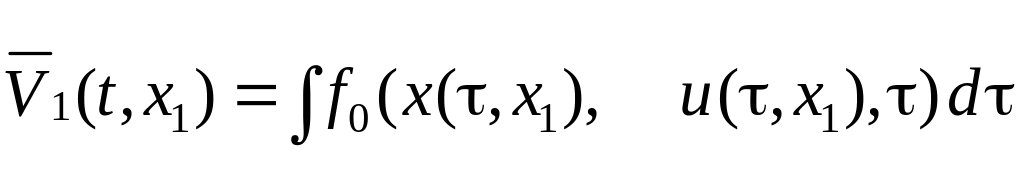. (6.283)

Пользуясь семейством решений, исключим из (6.283) вектор x₁, тогда получим функцию V₁(x, t). Затруднительным является построение семейства решений и, следовательно, самой функции V₁(x, t). С помощью функции V₁(x, t) строим управление u₂(x, t) так, чтобы оно доставляло функции

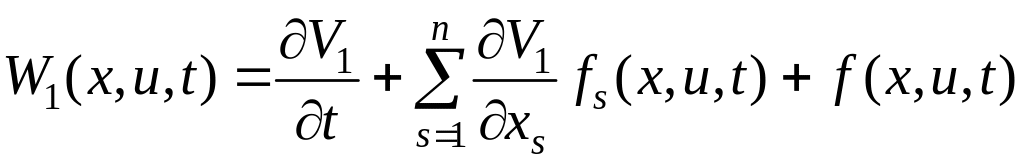
возможное наименьшее значение при условии выполнения ограничений (6.276), причем минимум ищется среди всех таких управлений, которые доставляют системе (6.275) нулевое асимптотически устойчивое решение. Если u₂(x, t) построено, то, поступая с ним как с V₁(x, t), найдем функцию V₂(x, t) и т. д. Если процесс построения оказывается возможным, то в результате получим минимизирующую последовательность u₁(x, t), u₂(x, t),…, такую, что

, (6.284)

где V_k(x₁,0) = J(u_k, x₁)..

Следовательно, u_1, u_2,… – минимизирующая последовательность для любой x₁.

Пусть система регулирования некоторым заданным объектом описывается с помощью дифференциальных уравнений

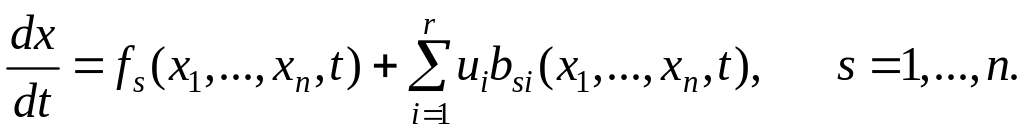(6.285)

Предположим, что управления u_{1 ,… ,} u_r удовлетворяют некоторым ограничениям:

(6.286)

Будем рассматривать движения системы, определенные на промежутке 0,Т. Следовательно, управления будем считать кусочно-непрерывными функциями, заданными на 0,Т.

Предположим, что качество управления определяется с помощью функционала J:

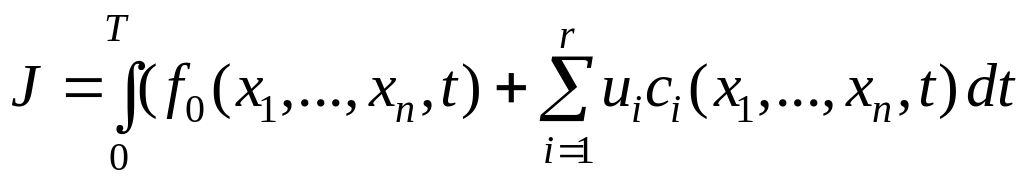(6.287)

и что задано начальное состояние системы

x = x₀ при t = 0.

Требуется среди указанных выше управлений найти такое, которое доставляет функционалу J возможное наименьшее значение. Такое управление будем обозначать через u₁⁽⁰⁾,…, u_r⁽⁰⁾ и называть оптимальным. Для решения этой задачи введем в рассмотрение функцию V(x₁,…, x_n, t), являющуюся решением уравнения в частных производных

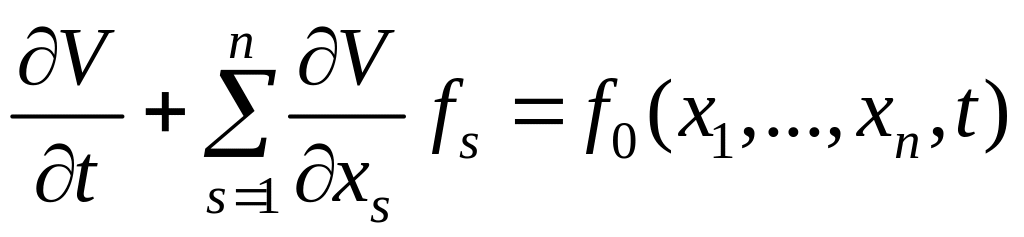(6.288)

с граничными условиями

V = 0 при t = T. (6.289)

Существование функции V может быть установлено с помощью следующего рассуждения. Рассмотрим левую часть уравнения (6.288) как полную производную функции V, вычисленную в силу уравнений

Тогда уравнение (6.288) может быть записано в виде

(6.290)

Найдем решение уравнения (6.290) с начальными условиями

при

Обозначим это решение через

(6.291)

Подставляя (6.291) в (6.290) и интегрируя с учетом условия (6.289), находим

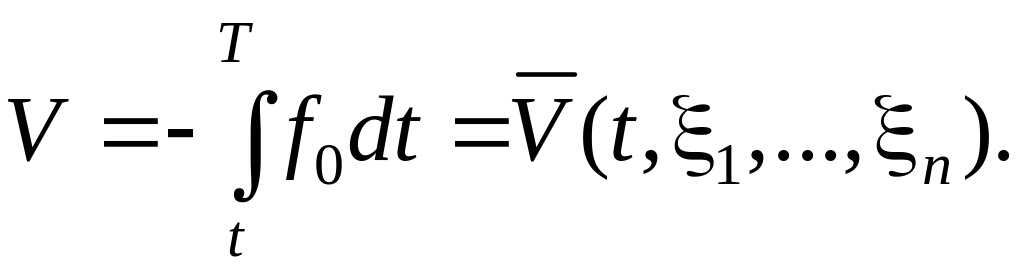(6.292)

Разрешая равенство (6.291) относительно ₁,…, _n, получим

(6.293)

Подставляя (6.293) в (6.292), получим функцию V(t, x₁,…, x_n,), которая будет удовлетворять уравнению (6.288) при условии (6.289). Итак, будем считать, что такая функция построена.

Перейдем к решению задачи. Рассмотрим функционал

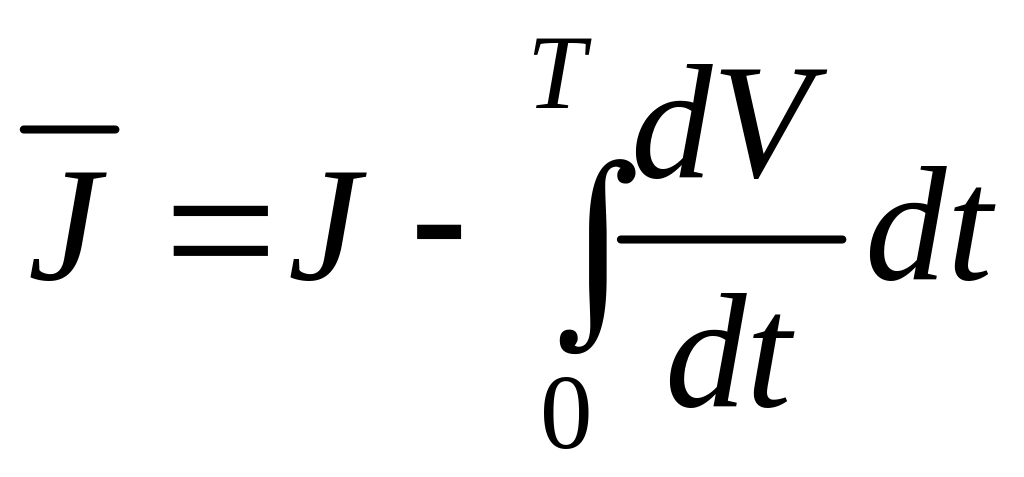. (6.294)

В функционале (6.294) полная производная от функции V берется в силу системы (6.285), следовательно,

откуда вытекает, что управления являются оптимальными по отношению к функционалу J и наоборот.

Проведем преобразования над функционалом J:

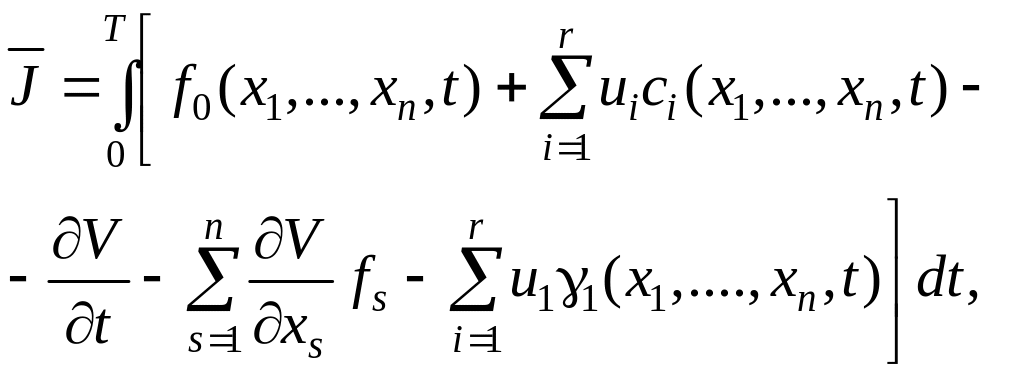(6.295)

где .

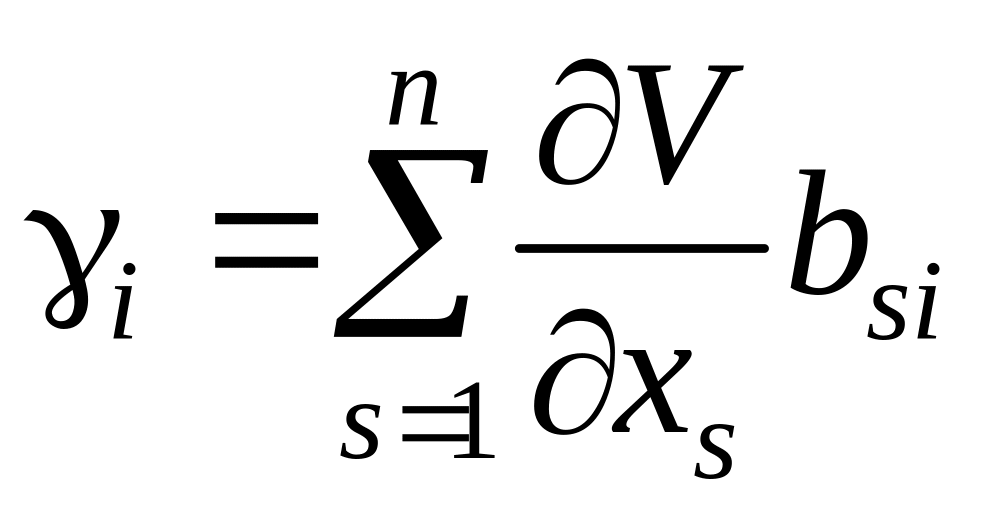Из уравнений (6.288) следует, что первый, третий и четвертый члены под интегралом в формуле (6.295) исчезают, следовательно, окончательно имеем

. (2.296)

Из (6.296) непосредственно вытекает, что оптимальное управление приближенно определяется формулами

. (6.297)

Эти формулы содержат в себе приближенное решение проблемы синтеза оптимального управления для того случая, когда правый конец траектории остается свободным.

Рассмотрим теперь проблему синтеза асимптотически устойчивых оптимальных управлений. Предположим, что система (6.285) при любом выборе кусочно-непрерывных управлений, удовлетворяющих условиям (6.286), имеет положительные равновесия:

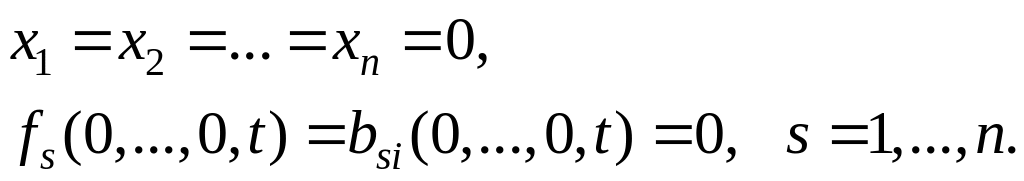
Будем считать это положение равновесия асимптотически устойчивым при u₁ =…= u _r = 0. Требуется выбрать управления u₁, …, u_r так, чтобы положение равновесия системы (6.285) было по-прежнему равномерно асимптотически устойчивым и чтобы функционал

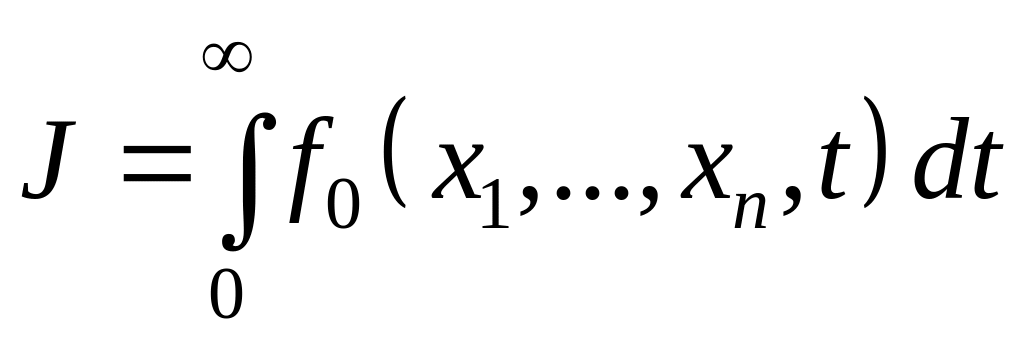(6.298)

имел наименьшее возможное значение, где f₀ (x₁, …, x_n, t) есть положительно определенная функция x₁, …, x_n. Для решения поставленной задачи рассмотрим функцию V, являющуюся решением уравнения (6.298) и удовлетворяющую условию

при . (6.299)

Известно, что решение уравнения (6.288) с начальным условием (6.289) существует, причем V является отрицательно определенной функцией.

Рассмотрим функционал

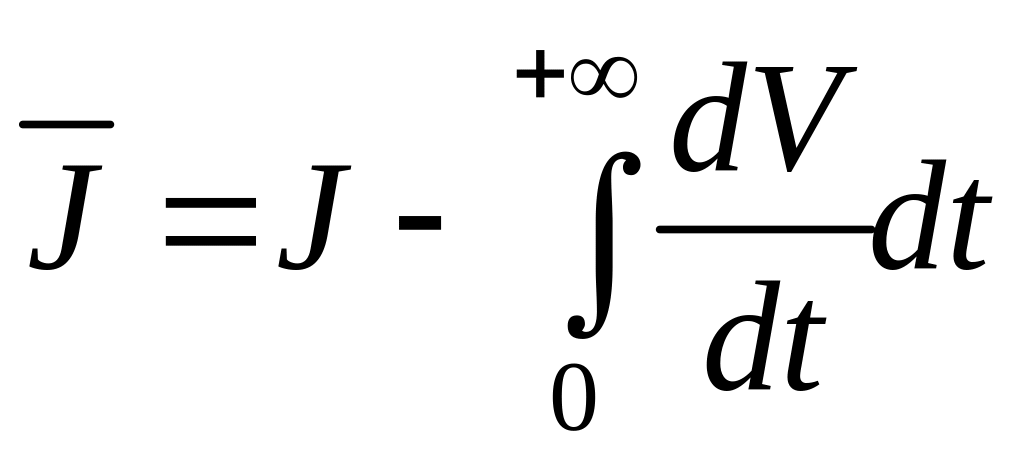. (6.300)

Полная производная функции V в функционале (6.300) берется в силу системы (6.285). Если управления u₁, …, u_r делают положение равновесия равномерно асимптотически устойчивым, то функционал J вполне определен и может быть представлен в виде

,

так как V  0 при t  +  .

Произведя преобразования над функционалом , получим

, (6.301)

откуда находим, что оптимальное управление будет приближенно определяться формулами

, (6.302)

где, как и выше

.

При управлении (6.302) положение равновесия системы (6.285) действительно будет равномерно асимптотически устойчивым, так как для этого управления

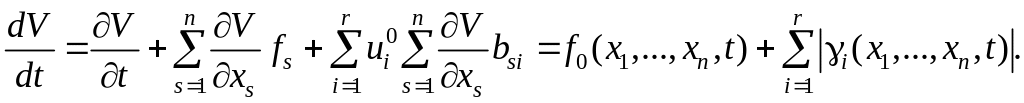Следовательно,

(6.303)

Функция V является отрицательно определенной, имеет бесконечно малый высший предел, ее полная производная в силу системы (6.285) положительно определена. Следовательно, нулевое решение системы (6.285) равномерно асимптотически устойчиво при управлении (6.302). Управления (6.297) и (6.302) могут быть построены лишь в том случае, когда известна функция V. Эту функцию можно строить путем последовательных приближений. Это обстоятельство приводит к методу последовательных приближений для отыскания управлений (6.297) и (6.302).

Остановимся сначала на случае конечного интервала. Пусть f₀ является полиномом степени l относительно x₁, …, x_n, а f_s – линейные функции:

. (6.304)

При этих условиях оказывается, что уравнение (6.288) имеет единственное решение V в виде полинома степени l, удовлетворяющее условию (6.289), причем определение функции V сведется к интегрированию линейных систем обыкновенных дифференциальных уравнений.

Если же в (6.304) r_s заменить рядом относительно x₁, …, x_n, в котором разложение начинается с членов второго порядка, то функция V также определится единственным образом в виде ряда.

Остановимся подробнее на случае (6.304). Будем искать решение уравнения (6.288) в виде

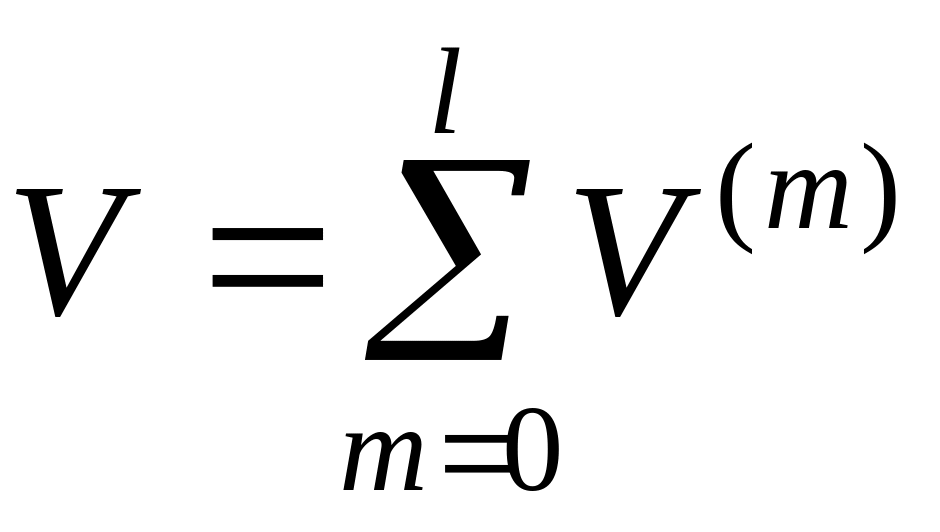. (6.305)

Полагая в (6.288)

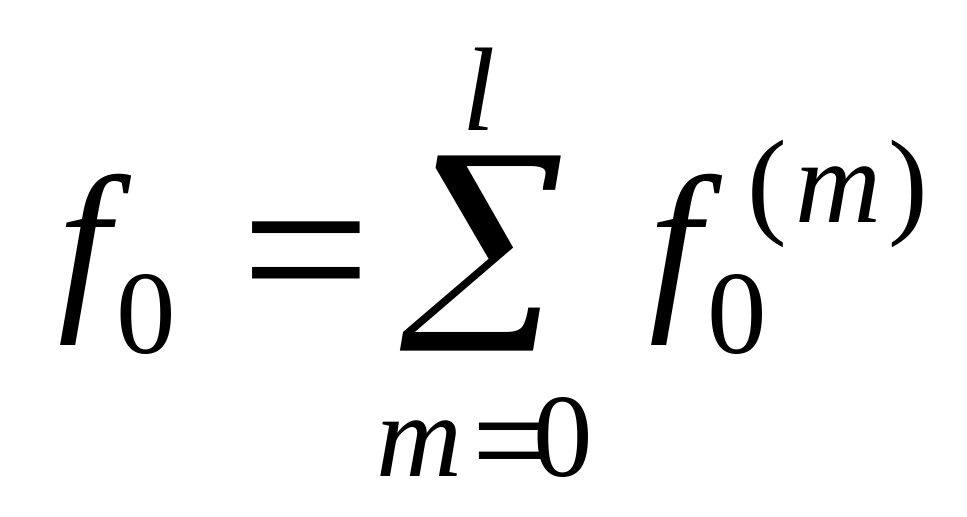, (6.306)

найдем

(6.307)

Для m = l имеем

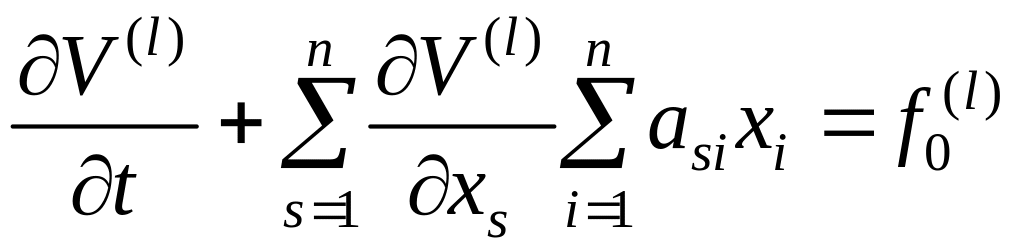. (6.308)

Формы V ^(m)  – удовлетворяют условиям

V ^(m) = 0 при t = T

Уравнения (6.307) и (6.308) получены путем подстановки в (6.288) выражений (6.305) и (6.306) и приравнивания слева и справа форм одинакового измерения. При этом частная производная заменена на полную, так как она относится только к коэффициентам форм. Из уравнений (6.307) и (6.308) вытекает, что коэффициенты искомых форм являются решениями неоднородных линейных дифференциальных уравнений с начальными условиями, заданными на правом конце при t = T, и, следовательно, определяются единственным образом.

Приведенные выше рассуждения позволяют дать метод последовательных приближений для определения функции V. Предположим, что задан полином V₁, например V₁  0. Построим последовательные приближения V_N как решения уравнений

с начальными условиями

V_N = 0, при t = T.

Следовательно,

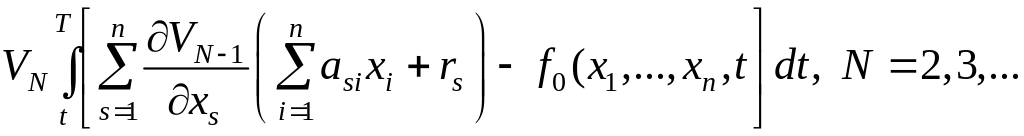(6.309)

Переменные x₁, …, x_n под интегралом в формуле (6.309) рассматриваются как параметры, следовательно, интегрирование относится лишь к функциям времени. Легко видеть, что 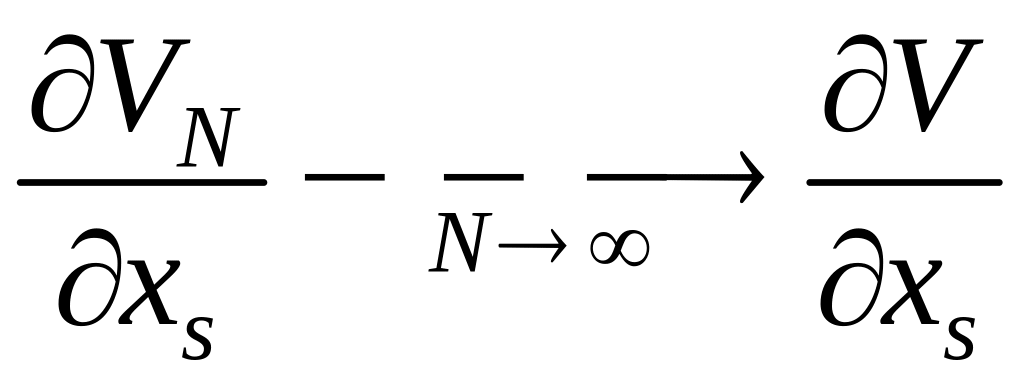равномерно по отношению к в любой ограниченной области изменения переменных x₁, …, x_n.

Положим

(6.310)

Ясно, что управления u_iN (i = 1,…, r) сходятся при    к управлению u_i⁽⁰⁾ (i = 1,…, r). Аналогичный метод последовательных приближений можно сформулировать для того случая, когда (6.305), (6.306) заменяются рядами относительно x₁, …, x_n, разложение которых начинается с членов не ниже второго порядка.

Рассмотрим теперь случай полубесконечного промежутка. Пусть

где  однородные формы степени m относительно x₁, …, x_n. Будем считать, что является положительно определенной квадратичной формой.

Предположим, что нулевое решение системы

(6.311)

равномерно асимптотически устойчиво. Тогда существует квадратичная форма V^(r), являющаяся отрицательно определенной и удовлетворяющая уравнению

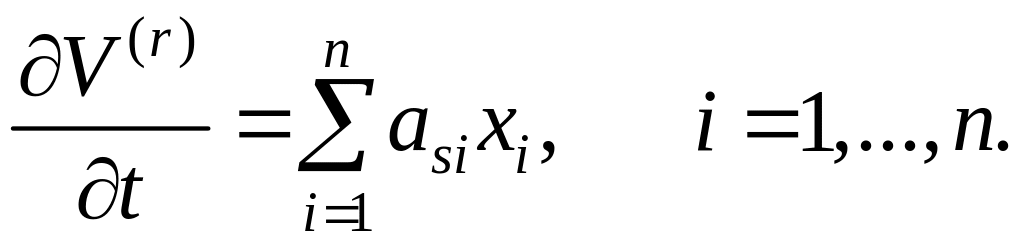(6.312)

Положим V₁ = V^(r), а приближение V_N определим как ограниченное решение уравнения

Здесь x₁, …, x_n. следует рассматривать как параметры. При известных предположениях относительно сходимости рядов f₀ и g_s можно утверждать, что

при N  

равномерно на всяком конечном интервале [0, T] в некоторой фиксированной окрестности положения равновесия, причем функция V здесь является отрицательно определенным решением уравнения (6.288). Отсюда вытекает, что последовательность управлений

,

где 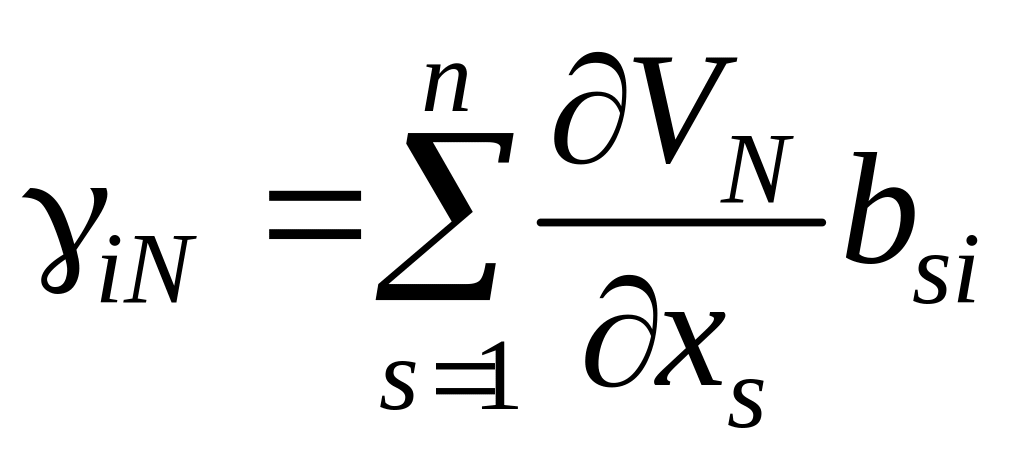, можно рассматривать как последовательность приближений для управлений (6.302).

Обратимся теперь к учету краевых условий и ограничений. Пусть требуется найти оптимальное управление по отношению к функционалу J среди всех тех управлений, для которых выполняются граничные и краевые условия

которые удовлетворяют ограничениям

Способ учета краевых условий и ограничений сводится к введению нового функционала

, (6.313)

где L_j и K_ (j = 1,…, k;  =1,…, ) – положительные величины, подлежащие определению. Функционал (6.313) можно представить в форме

(6.314)

Полная производная функция может быть представлена в виде

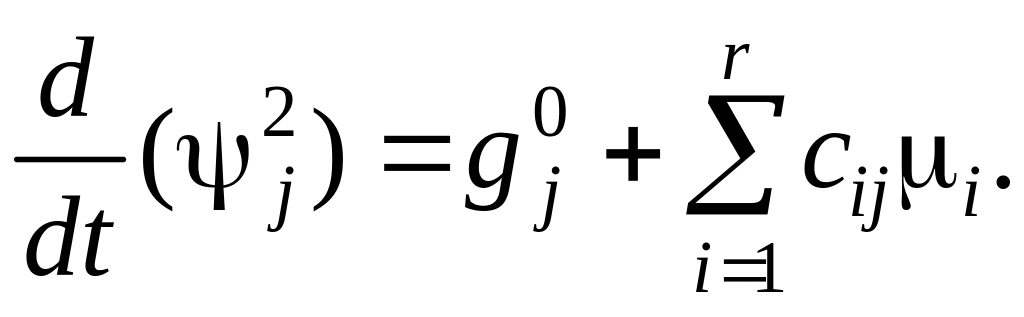
Рассмотрим функцию V, удовлетворяющую уравнению вида

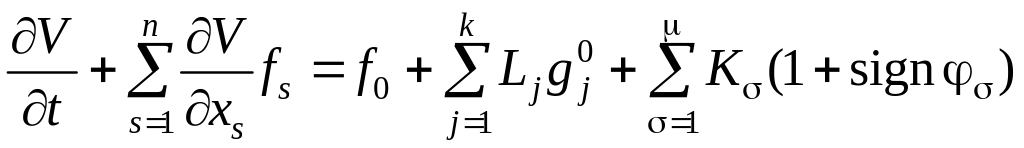(6.315)

и условию

V = 0 при t = T. (6.316)

Решение уравнений (6.315) при условии (6.316) можно искать в форме

где функция V₀ удовлетворяет уравнению (6.288) и условию (6.279), а функции V_1j и V_2 удовлетворяют соответственно уравнениям

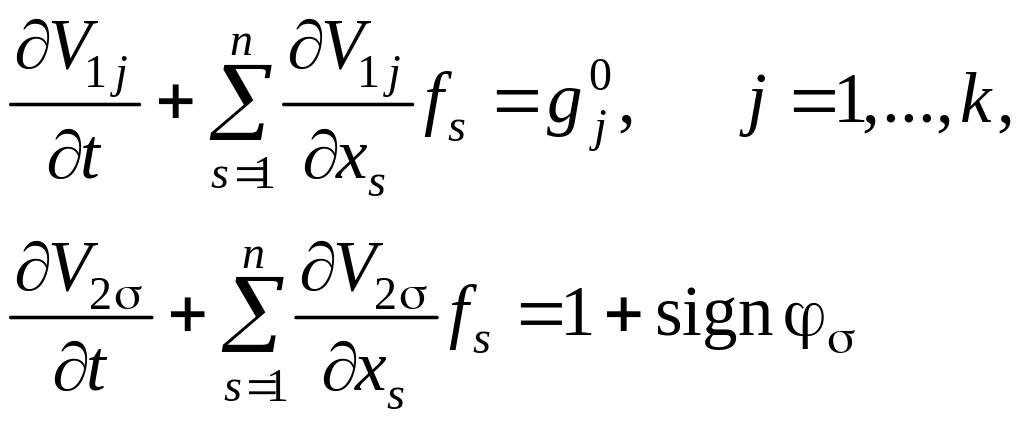
и краевым условиям

V_1j = V_2 = 0 при t = T, j = 1, …, k;  = 1, …, .

Предположим, что решение уравнения (6.135) при условии (6.316) найдено. Обозначим через (t, L₁, …, L_k, K₁, …, K_), i = 1, …, r управления, доставляющие функционалу L наименьшее возможное значение при условии, что правый конец свободен и ограничения не учитываются. Тогда это управление также будет оптимальным и по отношению к функционалу

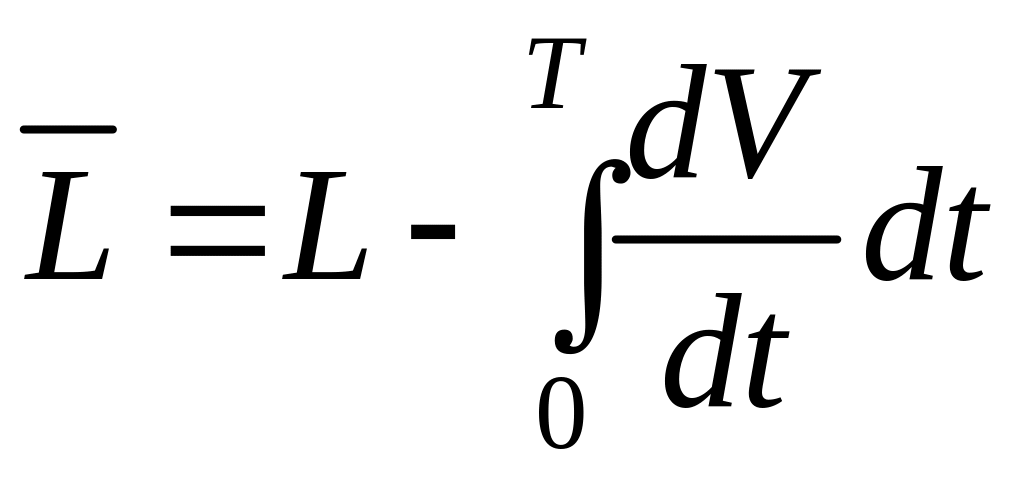. (6.317)

Произведя преобразования над функционалом (6.317), получаем

oткуда вытекает, что

, (6.318)

где

.

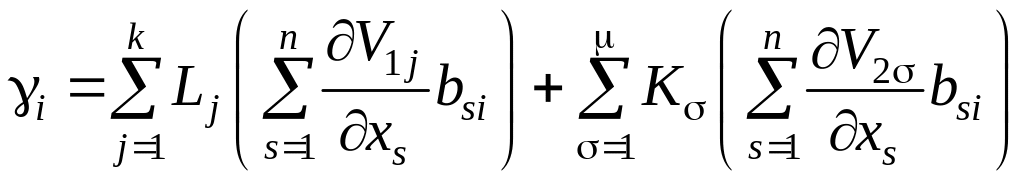Подставим управление (6.308) в функционал L и будем выбирать величины (L₁, …, L_k, K₁, …, K_), так, чтобы функционал L минимизировать. При этом в ряде случаев можно установить, что существуют такие последовательности величин (t, L₁, …, L_k, K₁, …, K_), которые позволяют сколь угодно точно аппроксимировать решение задачи с учетом краевых условий и ограничений, если такое решение существует.

В приведенных рассуждениях величина Т считалась закрепленной, однако предлагаемый метод последовательных приближений пригоден также для решения задачи и в случае незакрепленного Т.

Заметим, что выше нигде не были оговорены свойства функций, входящих в дифференциальные уравнения. Можно считать, что эти функции удовлетворяют условиям, при которых существует решение дифференциальных уравнений, и их даже можно отнести для простоты к дифференцируемым, принимающим вещественные значения и заданным при всех значениях аргументов, входящих в них. Из формул (6.297), (6.298), (6.318) вытекает, что управления разрывны по отношению к фазовым координатам. Это обстоятельство может привести к тому, что движения не будут определены в классическом смысле на всем рассматриваемом промежутке. Для того чтобы избежать этого, необходимо принять соглашение о скользящих режимах либо в окрестности поверхностей разрыва ввести гистерезисные петли, которые позволят однозначно определить движения на всем рассматриваемом промежутке. Управления с петлями гистерезиса будут весьма мало отличаться от построенных оптимальных.

Заметим, что в некоторых случаях формулы (6.297) и (6.302) определяют оптимальные управления. Например, это всегда имеет место для линейных задач с линейным функционалом. В общем случае рассмотренное построение служит для определения второго приближения, если в качестве первого взято нулевое управление.