Глава 6. Оптимальное управление

6.1. Общие понятия

Оптимальная система автоматического управления в определенном смысле обладает наилучшими свойствами.

Обычно задачи оптимального управления делят на два класса. Это задачи, связанные с построением оптимальной программы управления, и задачи синтеза замкнутых оптимальных систем.

Решить оптимальную задачу синтеза гораздо сложнее, чем задачу построения оптимальной программы управления.

При оптимизации системы всегда присутствует критерий оптимальности, который в математической форме отражает цель управления. Так, для достижения максимальной точности системы может служить минимум ошибки в виде интегрального квадратичного критерия:

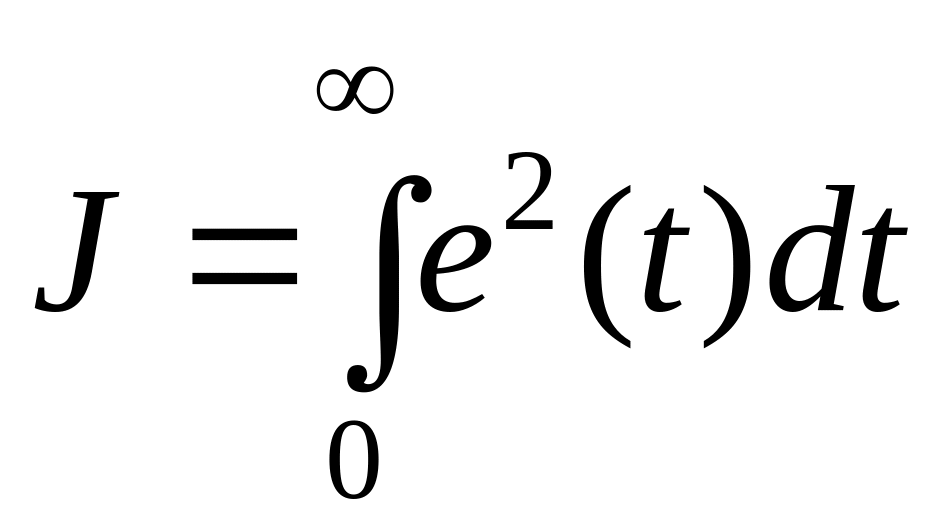, (6.1)

где e(t)  отклонение регулируемой величины от требуемого значения (ошибка регулирования).

Величина J называется функционалом, так как она зависит от выбора функций e(t), которую в свою очередь можно определить лишь после синтеза системы из условия минимума функционала J. Если целью системы управления является наиболее быстрый переход от одного состояния к другому, то в качестве критерия оптимальности используется

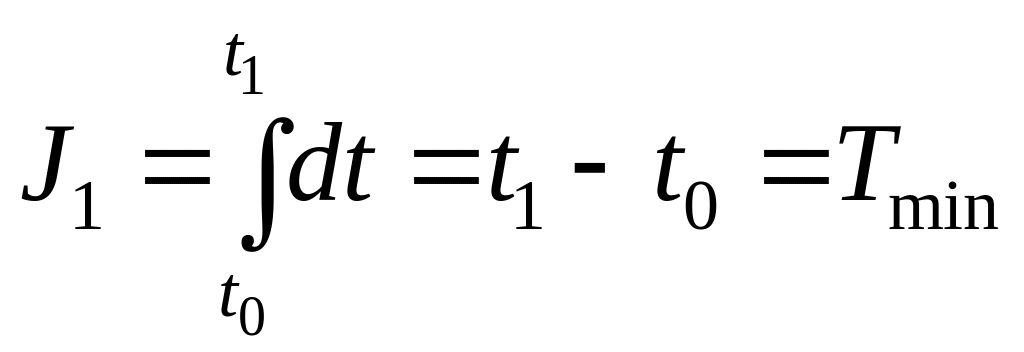. (6.2)

Функционал, минимум которого нужно получить, может представлять любую желаемую комбинацию оценок разных качеств системы.

Достаточно часто в качестве подынтегральной функции в критерии оптимизации используют положительно определенные квадратичные формы от фазовых координат x_i и управляющих воздействий U_q, где i, q .

Для систем дискретного типа операция интегрирования заменяется суммированием.

Если необходимо, чтобы система удовлетворяла нескольким критериям оптимизации, то в этом случае существенно усложняется задача синтеза оптимальной системы в сравнении с синтезом на основе одного критерия.

Для технических систем автоматического управления всегда характерно наличие значительного числа ограничений на переменные и соответственно на составляющие критериев оптимизации и переменные модели движения объекта управления.

Задача оптимального управления формируется следующим образом. Из множества допустимых управлений требуется выбрать такое, которое переводит объект управления из начального положения в конечное и минимизирует функционал качества. Такое управление и соответствующая траектория движения объекта называются оптимальными.

Свобода выбора оптимальных управляющих воздействий существенно ограничивается допустимым диапазоном изменений фазовых координат и управляющих воздействий, условиями в виде голономных связей

, (6.3)

неголономных связей

(6.4)

и изопериметрических ограничений в виде функционалов

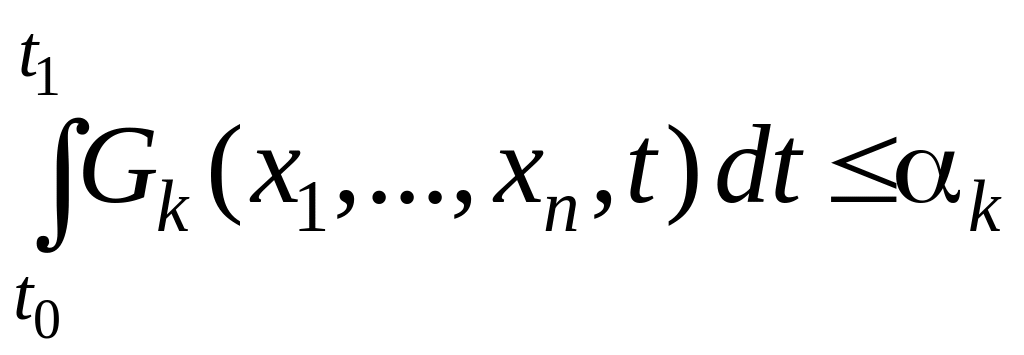. (6.5)

Существуют различные способы оптимизации. В основе большинства способов лежат математические вариационные методы. Оптимальные законы управления, учитывающие имеющиеся ограничения, часто получаются нелинейными.

6.2. Вариационное исчисление в оптимальном управлении

В вариационном исчислении традиционно выделяются задачи Лагранжа, Майера и Больца.

В задаче Лагранжа имеем интегральный критерий оптимизации вида

(6.6)

при ограничениях типа системы дифференциальных уравнений

. (6.7)

В задаче Майера критерий оптимизации имеет вид

(6.8)

при ограничениях (6.7) и системе конечных условий

. (6.9)

Задача Больца включает задачи Лагранжа и Майера.

Рассмотрим задачу Лагранжа в виде минимизации интеграла:

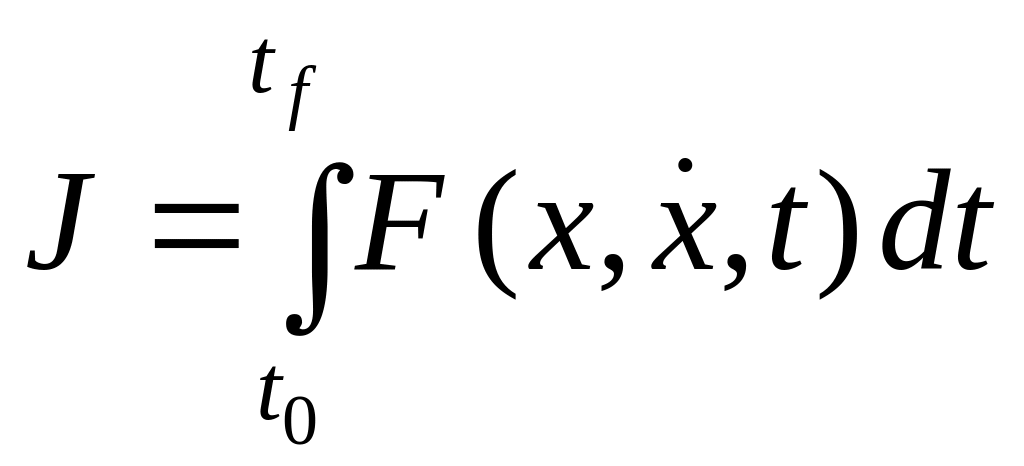. (6.10)

Требуется найти функцию x(t), минимизирующую интеграл (6.10).

Пусть x(t)  функция, обеспечивающая минимум, а   функция близкая к x(t). Тогда x(t) и связаны соотношением

(6.11)

где e  малый параметр; (t)  произвольная функция, для которой

. (6.12)

Заменяя x и в интегральном критерии соответственно на и , имеем

.

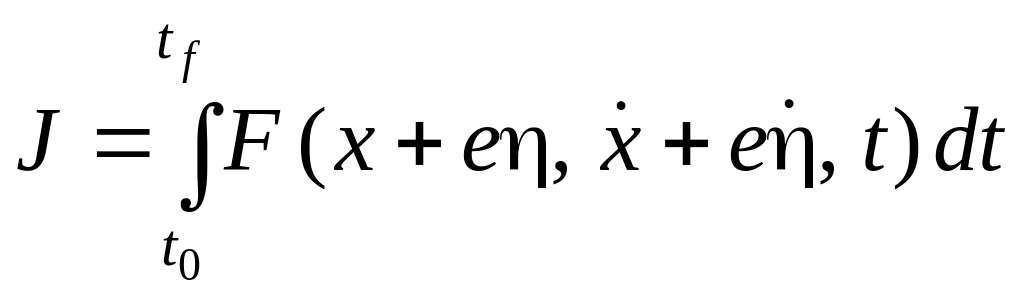Разлагая подынтегральное выражение в ряд Тейлора и пренебрегая нелинейными составляющими ряда, имеем

.

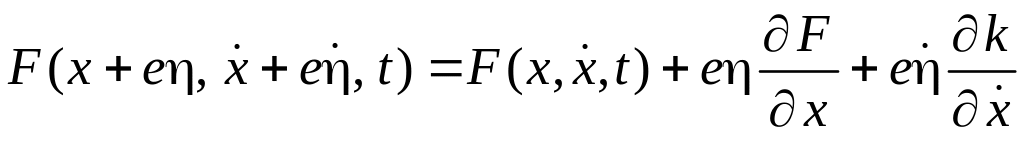Интегральный критерий перепишем в виде

. (6.13)

Необходимым условием для нахождения экстремума функции J является

dJ/de = 0. (6.14)

Откуда следует

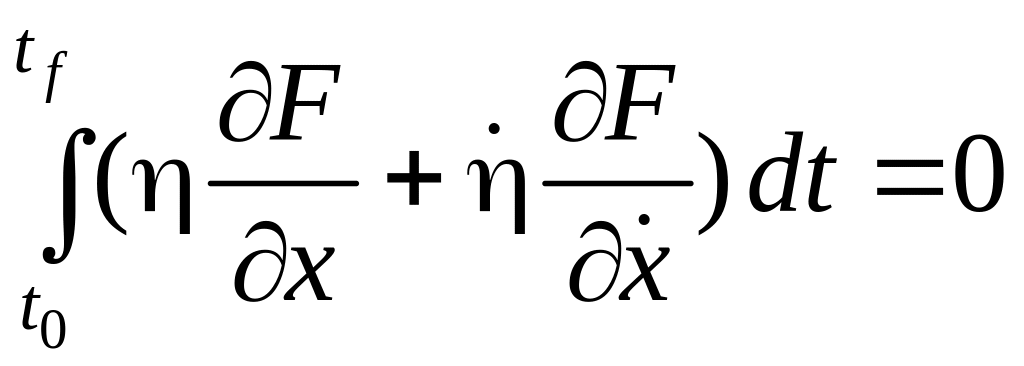. (6.15а)

Интегрирование по частям второго члена в этом интеграле

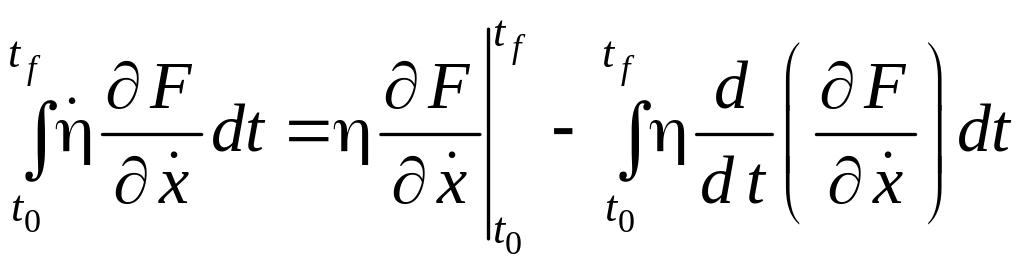(6.15б)

приводит к выражению

. (6.15в)

Используя данную зависимость в условии для экстремума, имеем

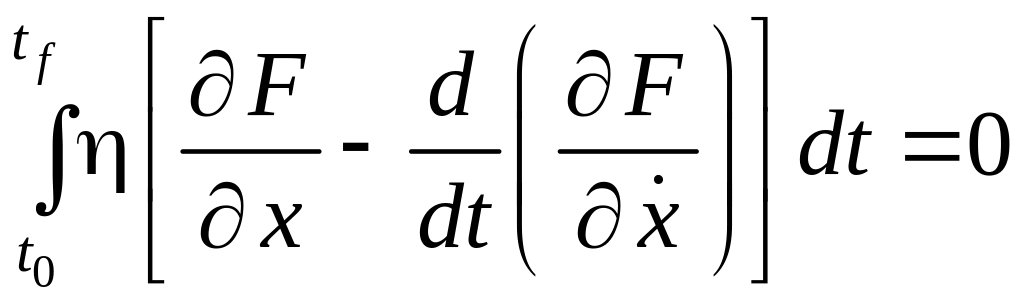. (6.15г)

Откуда следует уравнение Эйлера:

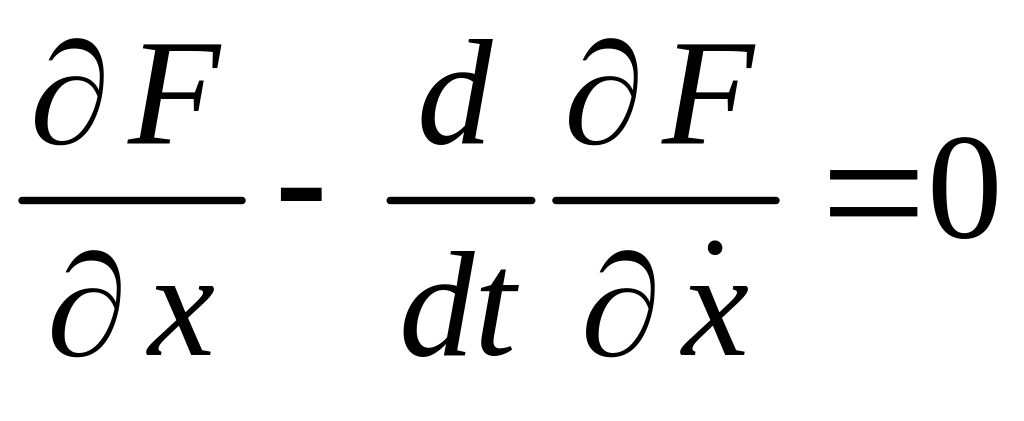, (6.16)

решение которого в большинстве случаев определяет функцию, доставляющую экстремум J. Данное условие соответствует задаче с закрепленными точками x(t₀) и x(t_f). Если закреплена точка x(t₀), а точка x(t_f) лежит на кривой с(t), то уравнение Эйлера дополняется условием трансверсальности:

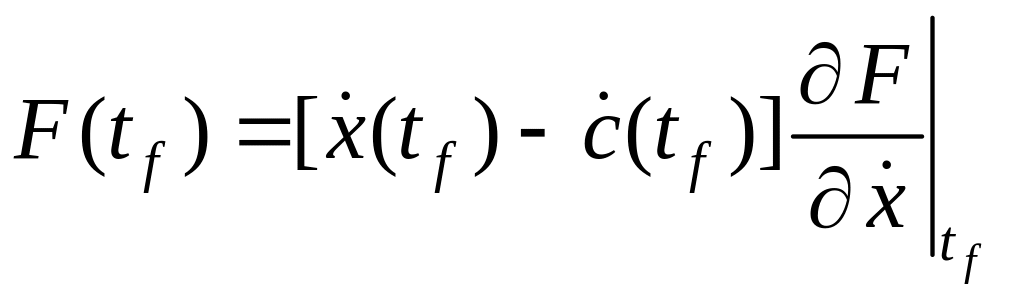. (6.17)

Рассмотрим примеры использования уравнения Эйлера. Пусть требуется найти функцию x(t), которая минимизирует функционал

.

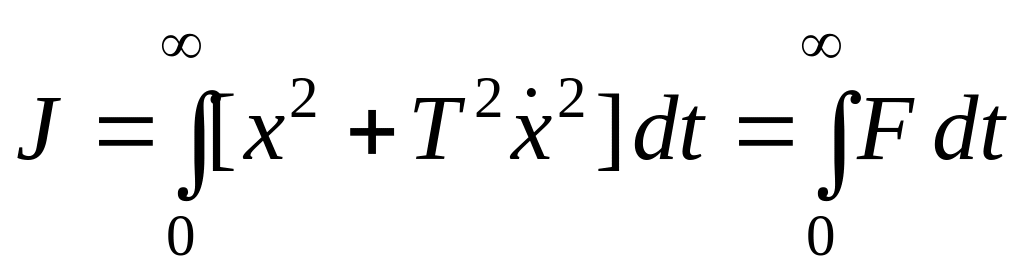Находим производные

.

Подставляя производные в уравнение Эйлера, имеем уравнение

,

решение которого запишем в виде

.

Если процесс в системе затухает, то при с₂ = 0, с₁ = х(0) переходный процесс, минимизирующий функционал, описывается уравнением x(t) = x₀e ^{– t/T}.

Изменим критерий качества

.

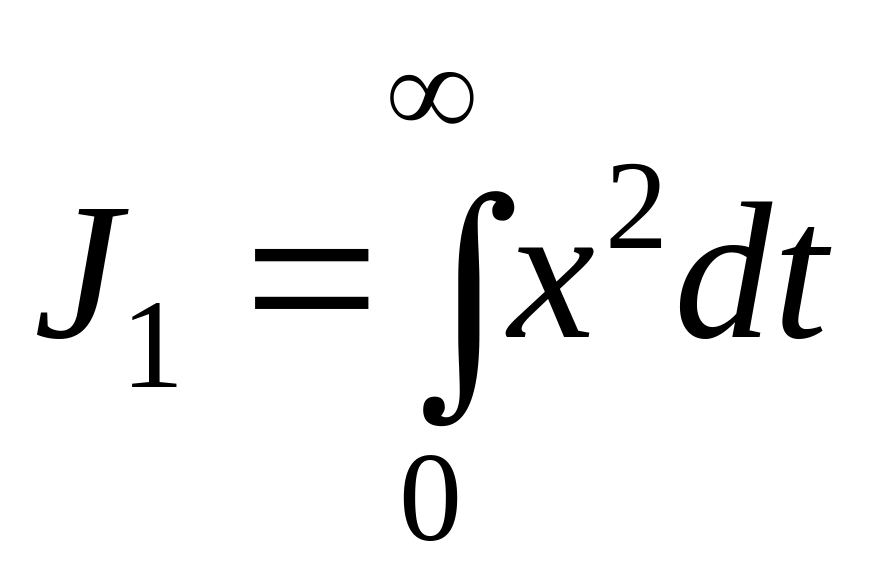В этом случае уравнение Эйлера вырождается в алгебраическое уравнение:

2x(t) = 0.

Если х(0)  0, то обеспечить в системе управления мгновенное устранение отклонения можно лишь при использовании чрезмерно больших управляющих воздействий.

Вариационные методы применимы, если функции, обеспечивающие экстремум, можно дифференцировать. Управляющие воздействия современных систем могут изменяться, например, по релейному закону, что исключает в этом случае использование вариационного исчисления для решения таких задач.