6.2 Розрахунок розмірних ланцюгів імовірнісним методом

Цей метод ґрунтується на відомому положенні теорії ймовірності, згідно з яким граничні значення (найбільше, найменше) розмірів усіх складових ланок розмірного ланцюга зустрічаються значно рідше, ніж їх середні значення.

Замикаючу ланку розмірного ланцюга розглядають як випадкову величину, яка є сумою незалежних (за величиною відхилень) складових ланок ланцюга.

Приймають, що , де – діапазон розсіювання похибок для кожної із ланок ланцюга (вважають, що похибки підпорядковуються законові нормального розподілу). Відповідно для замикаючої ланки

; (6.12)

. (6.13)

Граничні відхилення складових ланок розраховують за середнім відхиленням (координатою середини поля допуску ):

. (6.14)

; (6.15)

. (6.16)

Для замикаючої ланки:

; (6.17)

; (6.18)

; (6.19)

, (6.20)

де координати середини полів допусків ланок (замикаючої, збільшуючих, зменшуючих) розмірного ланцюга.

В оберненій задачі визначають: , , , (див. ф-ли 6.13, 6.20, 6.18, 6.19).

При розв’язуванні прямих задач застосовують ті ж способи, що і в розрахунках методом повної взаємозамінності, а саме спосіб рівних допусків:

, (6.21)

й спосіб допусків однакової точності:

. (6.22)

Визначивши допуски складових ланок розмірного ланцюга , підбирають значення розмірів , виходячи з умови 6.19 якщо

, (6.23)

, (6.24)

Застосування імовірнісного методу розрахунку розмірних ланцюгів порівняно з методом повної взаємозамінності дозволяє:

• при розв’язуванні прямої задачі за заданим допуском замикаючої ланки призначити більш грубі допуски складових ланок, які технологічно легше виконувати;

• при розв’язуванні оберненої задачі за відомими допусками складових ланок визначити більш вузький, але більш ймовірний діапазон розсіювання або допуск замикаючої ланки.

Недоліки методу:

• відсутність повної гарантії від браку за точністю замикаючої ланки;

• відносна складність і велика трудомісткість обчислювальних робіт;

• точність і достовірність розрахунків залежать від точності й достовірності визначення статистичних характеристик розподілу.

6.3 Приклад розв’язування задачі

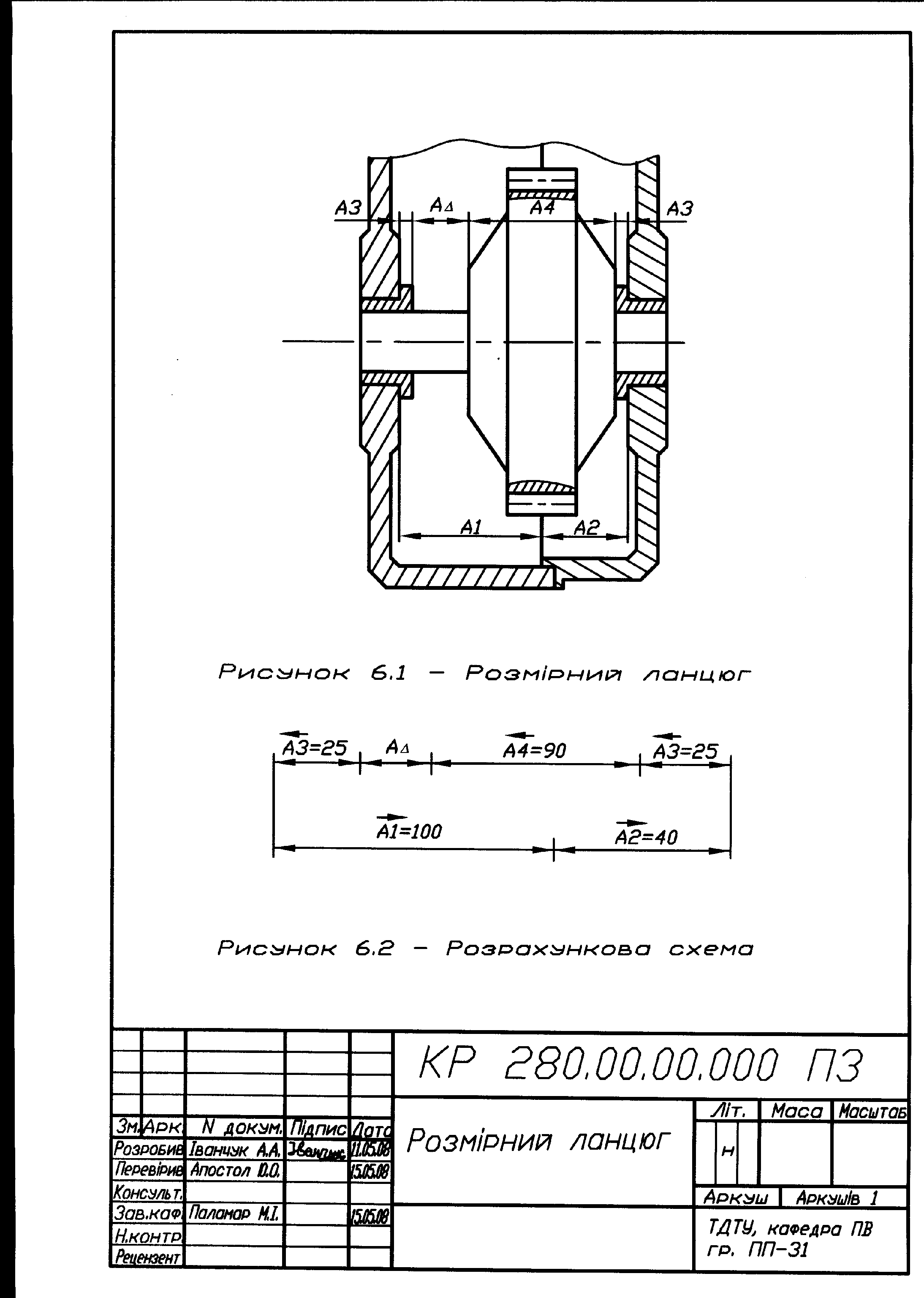
Для заданого розмірного ланцюга (рис. 6.1) призначити допуски складових ланок: А₁=100 мм, А₂=40 мм, А₃=25 мм (дві ланки див. рис. 6.1), А₄=90 мм, якщо відомо граничні відхилення замикаючої ланки

мкм,

мкм.

Розв’язування

Метод повної взаємозамінності

Будуємо розрахункову схему розмірного ланцюга (рис. 6.2) й для зручності результати обчислень записуємо в таблицю 6.1 (зауважимо, що розмірний ланцюг містить дві ланки А₃=25 мм див. рис.6.1).

Розв’язуємо пряму задачу методом повної взаємозамінності. Оскільки складові ланки входять в різні інтервали, то застосовуємо спосіб допусків однакової точності.

Розраховуємо допуск замикаючої ланки розмірного ланцюга як різницю її граничних відхилень ( мкм, мкм)

,

мкм.

Одиниці допуску складових ланок знаходимо за таблицею 6.3. Визначаємо суму цих одиниць (врахувавши значення і для двох ланок А₃)

=2,17+1,56+1,31+2,17+1,31=8,52 мкм.

За формулою 6.9 обчислюємо коефіцієнт точності розмірного ланцюга

,

.

Його значення ( ) відповідає 6 квалітету точності (див. табл.6.4). Згідно з ДСТУ 2500–94 знаходимо допуски складових ланок розмірного ланцюга.

Таблиця 6.1– Результати розрахунків методом повної взаємозамінності

Номінальні значення розмірів , мм	Одиниця допуску і, мкм	Допуск розміру , мкм	Розміри складових ланок , мм (прийняті)
А1=100	2,17	22
А2=40	1,56	16	40+0,016
А3=25	1,31	13	25–0,013
А3=25	1,31	13	25–0,013
А4=90	2,17	22	90–0,022

Для охоплюючого розміру А₂ (див. розрахункову схему рис. 6.2) допуск проставляємо як для основного отвору (тобто у ”+”), а для охоплюваних А₃, А₄ як для основного вала (тобто у ”–”).

Граничні відхилення розміру А₁ визначаємо за формулами 6.4–6.5:

;

;

Отримуємо ;

;

;

Допуск ланки А₁

;

мкм.

Перевіряємо виконання умови 6.11:

;

мкм;

мкм;

80 мкм=80 мкм.

Імовірнісний метод розрахунку

Розрахунок проводимо за таблицею 6.2 (стовбці 1, 2 такі ж, як в табл. 6.1), з якої отримуємо

=15,25 мкм.

Таблиця 6.2 – Результати розрахунків імовірнісним методом

Номінальні значення розмірів , мм	Одиниця допуску і, мкм	і2, мкм2	Допуск розміру , мкм	ІТ2, мкм2	Допуск розміру , мкм	ІТ2, мкм2	Розміри складових ланок , мм (прийняті)
А1=100	2,17	4,7	35	1225	54	2916
А2=40	1,56	2,43	25	625	39	1521	40+0,039
А3=25	1,31	1,71	21	441	21	441	25–0,021
А3=25	1,31	1,71	21	441	21	441	25–0,021
А4=90	2,17	4,7	35	1225	35	1225	90–0,035
Сума		15,25		3957		6544

Допуск замикаючої ланки розмірного ланцюга ( мкм, мкм):

,

мкм.

Коефіцієнт точності розмірного ланцюга

,

.

Відповідно до отриманого значення приймаємо 7 квалітет точності для усіх ланок розмірного ланцюга. Згідно з ДСТУ 2500–94 знаходимо допуски розмірів (для 7-го квалітету й відповідного інтервалу).

За формулою 6.13 та даними табл.6.2 допуск замикаючої ланки дорівнює

,

мкм,

що є менше від заданого ( мкм).

Виходячи з конструктивних міркувань, для розмірів А₁, А₂ призначаємо допуски за 8 квалітетом точності, а для решти розмірів приймаємо 7 квалітет (див. 6, 7 стовбець табл.6.2). Тоді мкм – більше заданого.

Для охоплюючого розміру А₂ (див. розрахункову схему рис. 6.2) допуск проставляємо як для основного отвору (тобто у ”+”), а для охоплюваних А₃, А₄ як для основного вала (тобто у ”–”).

Граничні відхилення розміру А₁ визначаємо за формулами 6.14–6.20:

;

мкм.

Для ланки А₂ (див. 6.23):

;

,

а для охоплюваних розмірів А₃, А₄ (див.6.24):

;

.

За формулою 6.20 отримаємо

;

;

мкм;

Розраховуємо граничні відхилення ланки А₁ (див. рівності 6-15, 6.16)

;

мкм;

;

мкм.

Приймаємо мкм, мкм.

Таким чином, допуски складових ланок, визначені імовірнісним методом більш технологічні, ніж допуски, визначені методом повної взаємозамінності.

Таблиця 6.3 – Значення одиниці допуску для основних інтервалів розмірів

Інтервали номінальних розмірів, мм	Одиниця допуску і, мкм	Інтервали номінальних розмірів, мм	Одиниця допуску і, мкм
До 3	0,55	50–80	1,86
3–6	0,73	80–120	2,17
6–10	0,9	120–180	2,52
10–18	1,08	180–250	2,89
18–30	1,31	250–315	3,22
30–50	1,56	315–400	3,54

Таблиця 6.4

Позначення допуску	Величина допуску	Інтервали номінальних розмірів, мм	Величина допуску
ІТ5	7і	ІТ11	100і
ІТ6	10і	ІТ12	160і
ІТ7	16і	ІТ13	250і
ІТ8	25і	ІТ14	400і
ІТ9	40і	ІТ15	640і
ІТ10	64і	ІТ16	1000і