3 Электродинамическое действие токов кз

Силы взаимодействия проводников с током принято называть электродинамическими. В электрических машинах они широко используются для преобразования электрической энергии в механическую, однако при КЗ в электрических установках они могут привести к механическим разрушениям.

3.1 Взаимодействие параллельных проводников точечного сечения

Применим закон Био-Савара-Лапласа, согласно которому, на каждый элемент проводника 2 с током , находящегося в поле проводника 1 с током i₁, действует сила

, (28)

где - индукция в месте расположения элемента , - угол между векторами и . Направление силы перпендикулярно плоскости угла и определяется по правилу левой руки.

Индукция от воздействия тока i₁ в любой точке пространства может быть определена интегрированием

(29)

по всей длине проводника 1, где r – радиус, проведенный от элемента в точку наблюдения, - угол между направлениями векторов и . Направление индукции перпендикулярно плоскости угла и определяется по правилу буравчика.

Д ля случая, когда проводники параллельны и имеют бесконечную длину (рис.3.1)

Рисунок 3.1 – Взаимодействие параллельных проводников точечного сечения

Выразим B через H:

По закону полного тока :

; ; ; , Гн. (30)

где Гн/м - магнитная проницаемость вакуума.

Индукция B₁ постоянна вдоль проводника 2, следовательно, с учетом того, что , сила на длине проводника l равна:

(31)

3.2 Взаимодействие между тонкими полосами в параллельных плоскостях

Рассмотрим взаимодействие между элементами dy и dx полос, имеющих высоту поперечного сечения h.

Т оки этих элементов соответственно равны:

и

Как для проводников точечного сечения можно записать

Поскольку

и , то

Интегрируем

, (32)

где - коэффициент формы.

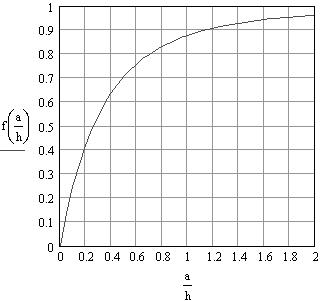
Рисунок 3.4 – Зависимость коэффициента формы от соотношения a/h

Коэффициент формы показывает, во сколько раз сила взаимодействия проводников конечного сечения отличается от силы взаимодействия бесконечно тонких проводников расположенных на том же расстоянии и с теми же токами. Чтобы определить К_ф для проводников конечного сечения необходимо разделить проводники на множество элементарных нитей и определить силу взаимодействия каждой нити одного проводника со всеми нитями другого и найти сумму этих сил.

3.3 Взаимодействие шин прямоугольного сечения

Э та достаточно сложная задача решена для проводников прямоугольного сечения в предположении равномерного распределения плотности тока по сечению проводника, т.е. без учета поверхностного эффекта и эффекта близости.

Р

Рисунок 3.5 – К определению сил взаимодействия между шинами прямоугольного сечения

азбиваем каждую шину на тонкие полосы, как показано на рис.3.5, тогда токи полос будут равны и , а силу их взаимодействия можно найти с помощью (32).

Сила, действующая на полосу толщиной dx, будет равна сумме сил ее взаимодействия со всеми элементарными полосами второго проводника:

.

Искомую силу, действующую на весь проводник, найдем как сумму сил, действующих на его элементарные полосы

, (33)

где .

При b = 0 .

При ≥ 2 , т.е. силы взаимодействия в этом случае можно определять по выражению (30), справедливому для бесконечно тонких проводников.

Рисунок 3.6 – Коэффициент формы проводников прямоугольного сечения

Коэффициент формы для круглых сплошных проводников, а также для проводников кольцевого сечения равен 1.