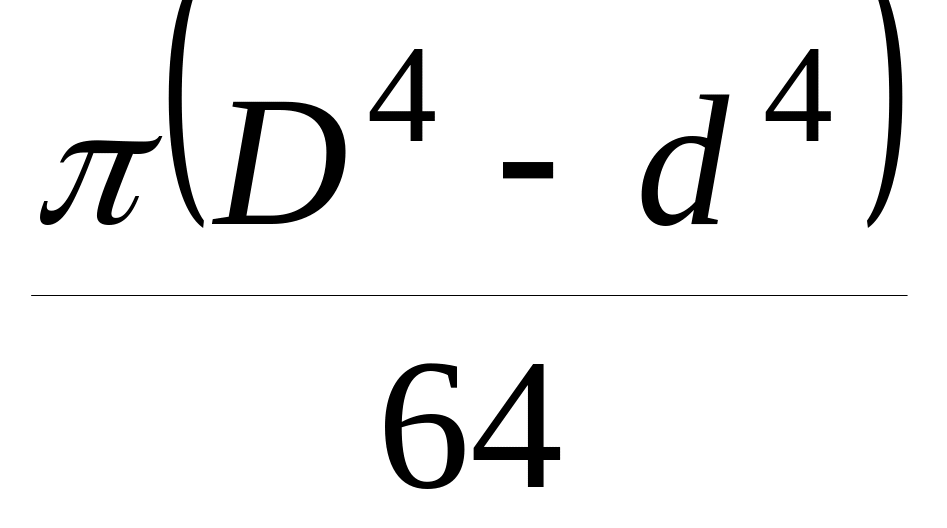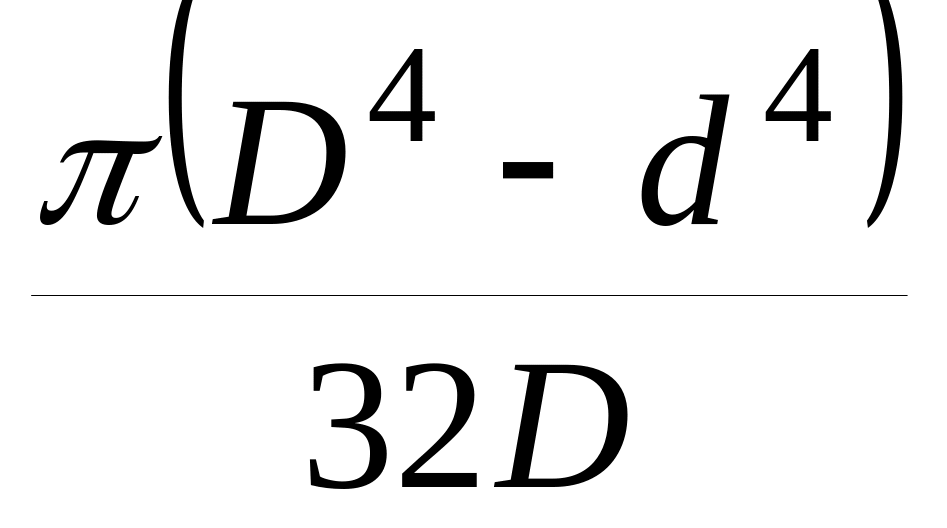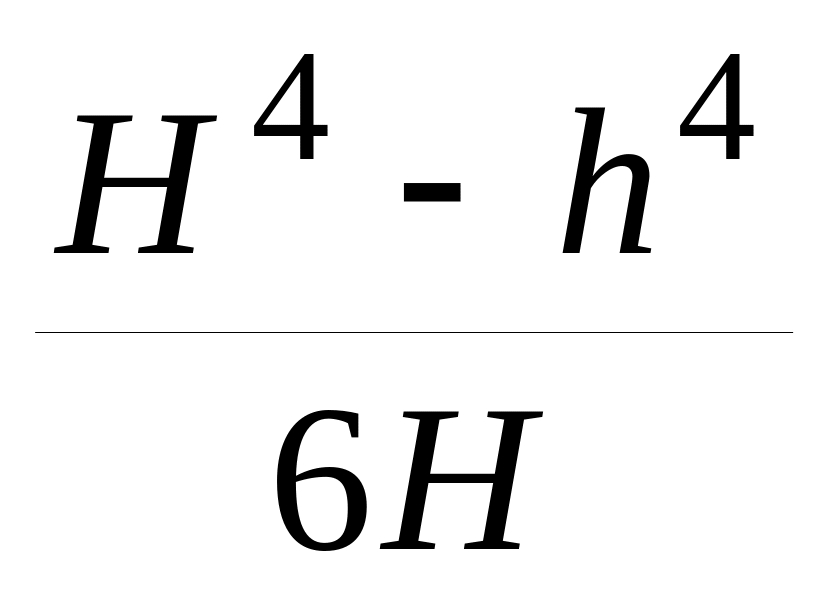3.7 Взаимодействие шин при трехфазном кз

В соответствии с (34) при = 90º токи фаз будут иметь вид:

Направим токи фаз так, как если бы ток фазы A возвращался по фазам B и C (рис. 3.12), а силы – как результат отталкивания проводников друг от друга.

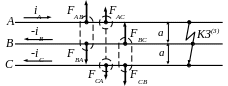
Рисунок 3.12 – Взаимодействие шин при трехфазном КЗ

Силы взаимодействия определяются по формуле (2.31):

Силы F_A, F_B, F_C, имеют наибольшие значения при одних и тех же условиях, когда = -15, 75, 165 или 255˚. Рассмотрим токи фаз при = -15˚. При этом угле включения ток фазы A наиболее близок к рассмотренному случаю двухфазного КЗ.

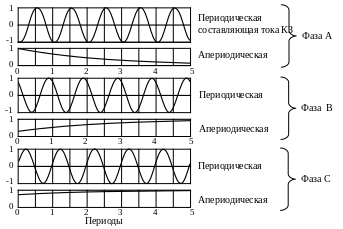
Рисунок 3.13 – Составляющие токов фаз при трехфазном КЗ для = -15˚

Важно отметить, что ток фазы A протекает в прямом направлении к точке КЗ и возвращается, разделившись на токи фаз B и C. На рисунке 3.13 это выполняется как для периодических, так и для апериодических составляющих токов фаз. Таким образом, если расположить проводник фазы C в непосредственной близости к фазе B, то на фазу A будут действовать силы, как при двухфазном КЗ (рис. 3.11).

При удалении фазы C на расстояние 2a от фазы А, сила их взаимодействия уменьшится в 2 раза (рис. 3.14), что снизит результирующее максимальное значение силы F_A до

. (38)

Можно отметить также, что на очень небольших промежутках времени сила меняет знак, но общий характер – отталкивание.

В силу симметрии системы шин .

В наиболее тяжелых условиях будет находится шина В (рис.3.15). С одной стороны на нее действует такая же сила взаимодействия F_AB = – F_BA, как и на шину А, но, с другой стороны, сила взаимодействия с фазой С велика, вследствие ее близкого расположения.

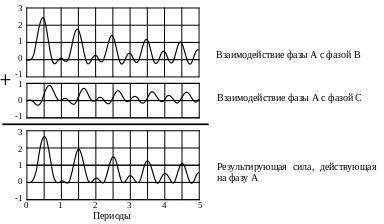
Рисунок 3.14 – Силы, действующие на фазу A

Усилия, прилагаемые к фазе B, носят выраженный знакочередующийся характер и имеют большой размах колебаний. Максимальное усилие

. (39)

больше, чем для фазы A.

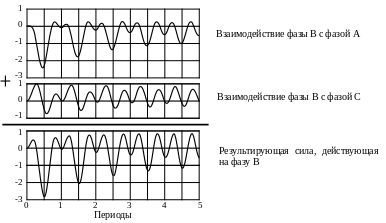
Рисунок 3.15 – Силы, действующие на фазу B

Т

Периоды

аким образом, шины фаз отталкиваются друг от друга.

Сила взаимодействия между проводниками при трехфазном КЗ больше, чем при двухфазном. Действительно, так как при удаленных КЗ соотношение токов

, то .

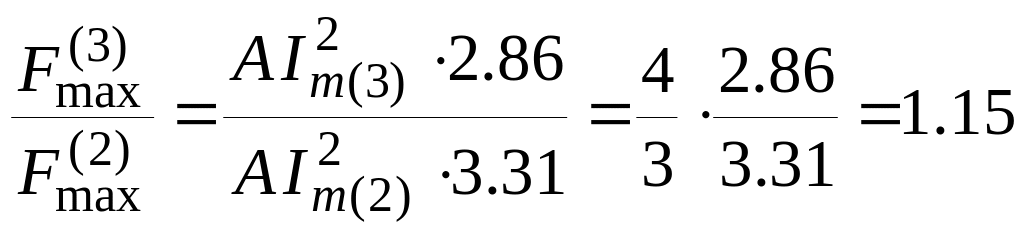Поэтому трехфазное КЗ является расчетным видом КЗ при проверке проводников и аппаратов на электродинамическую стойкость.

3.8 Расчет шин на электродинамическую стойкость

Шинная конструкция, состоящая из шин, изоляторов и основания, к которому прикреплены изоляторы, представляет собой упругую систему, которая под действием электродинамических сил приходит в сложное колебательное движение. При этом нагрузка от шин передается изоляторам. Критериями механической прочности (электродинамической стойкости) являются максимальные напряжения в материале шин и максимальные нагрузки на изоляторах, которые не должны превышать допустимые.

Как было показано в предыдущем разделе, на шины действует 50-герцовая составляющая силы – до затухания апериодической составляющей тока и 100-герцовая – все время действия КЗ. Если собственные частоты колебательной системы совпадут с этими значениями, система накопит энергию и амплитуда колебаний значительно превысит смещение шин от такой же величины, но статической нагрузки. Процесс аналогичен раскачиванию качелей: периодически прилагая небольшое усилие можно достичь большой амплитуды качаний. В то же время приложение такого же, но постоянного во времени усилия, приведет лишь к небольшому отклонению качелей.

Если собственные частоты меньше 30 и больше 200 Гц, то механического резонанса не возникает, и могут быть приняты следующие допущения, позволяющие значительно упростить задачу:

1. Шинная линия представляется статической системой, в которой не учитываются колебания шин и изоляторов.

2. Нагрузка равномерно распределена по длине пролетов между изоляторами.

3. Шины свободно лежат на опорах и расположены в одной плоскости.

Рисунок 3.16 – Расчетная схема шины, свободно лежащей на опорах (а); б – стержень с защемленными концами; в – стержень со свободными концами

Касательные к изогнутой оси шины во всех точках крепления, кроме крайних, совпадают с недеформированной осью шины. Отсюда следует, что пролет шины можно рассматривать как стержень с защемленными концами (рис. 3.16). Однако крайние участки шин имеют один защемленный, а второй свободный концы, поэтому в качестве расчетного значения принимают среднее значение момента

,

где f – равномерно распределенная сила, H/м; l – длина пролета, м.

Момент инерции поперечного сечения определяет свойство шины сопротивляться искривлению в зависимости от формы и размеров поперечного сечения. Модуль упругости характеризует то же свойство шины сопротивляться искривлению, но в зависимости от свойств материала. Произведение EJ называется жесткостью шины при изгибе. Чем больше жесткость шины, тем меньше ее прогиб под действием изгибающего момента.

Таблица 3.1 – Механические характеристики материала шин

Материал	Марка	Разрушающее напряжение, σразр, МПа	Допустимое напряжение, σдоп, МПа	Модуль упругости, E, Па
Алюминий	АО, А1	120	80	7·1010
	АДО	60 – 70	40	7·1010
Алюминиевый сплав	АД31Т	130	75	-
	АД31Т1	200	90	-
Медь	МГТ	250 – 300	140	10·1010
Сталь	Ст 3	370 – 500	160	20·1010

Методика расчета.

П

ри проектировании РУ с жесткими шинами производится определение частоты собственных колебаний, которые для алюминиевых шин определяются по формуле:

, для медных – ,

где l – длина пролета между изоляторами, м; J – момент инерции поперечного сечения относительно оси, перпендикулярной направлению изгибающей силы, см² ; q – поперечное сечение шины, см².

Если полученная частота попадает в опасную область 30 < f₀ < 200 Гц, то, изменяя длину пролета и форму сечения шин, добиваются выхода из области резонанса. Далее предполагается, что система является статической, с нагрузкой, равной максимальному усилию, возникающему при КЗ.

Напряжение в материале шин, возникающее под действием изгибающего момента

, МПа,

где M – изгибающий момент, Н·м; W – момент сопротивления поперечного сечения шины относительно оси, перпендикулярной действию силы, см³, определяется по таблице 3.2.

При трехфазных КЗ удельная сила, действующая на проводник фазы B

, Нм.

Тогда , МПа.

Шины механически прочны, если – расчетное напряжение в материале шин меньше допустимого (табл. 3.1). В электроустановках широко применяют шины прессованные из алюминиевого сплава, закаленные и естественно состаренные (марка АДЗ1Т) или закаленные и искусственно состаренные (марка АДЗ1Т). Согласно ПУЭ .

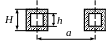
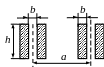
Таблица 3.2 – Моменты инерции и сопротивления

Р асположение шин	Момент инерции, J, см4	Момент сопротивления, W, см3
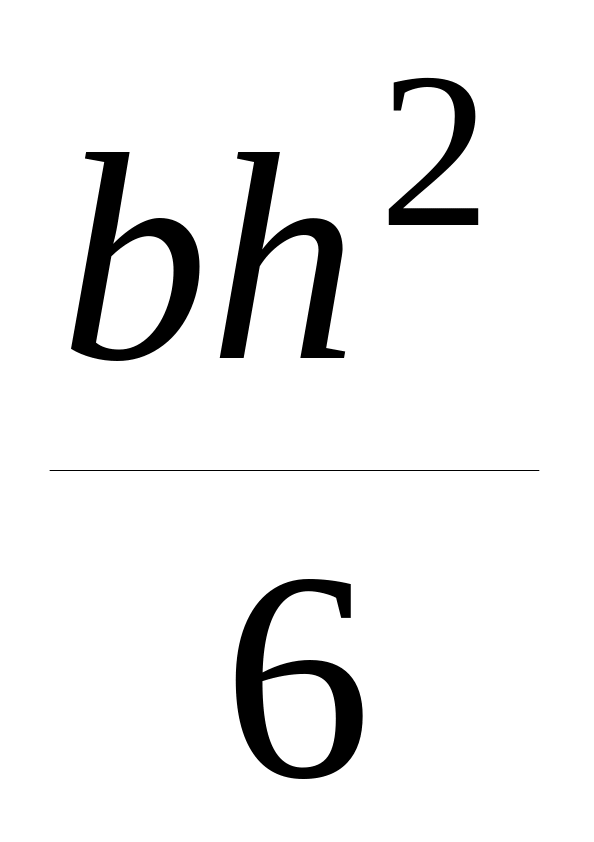
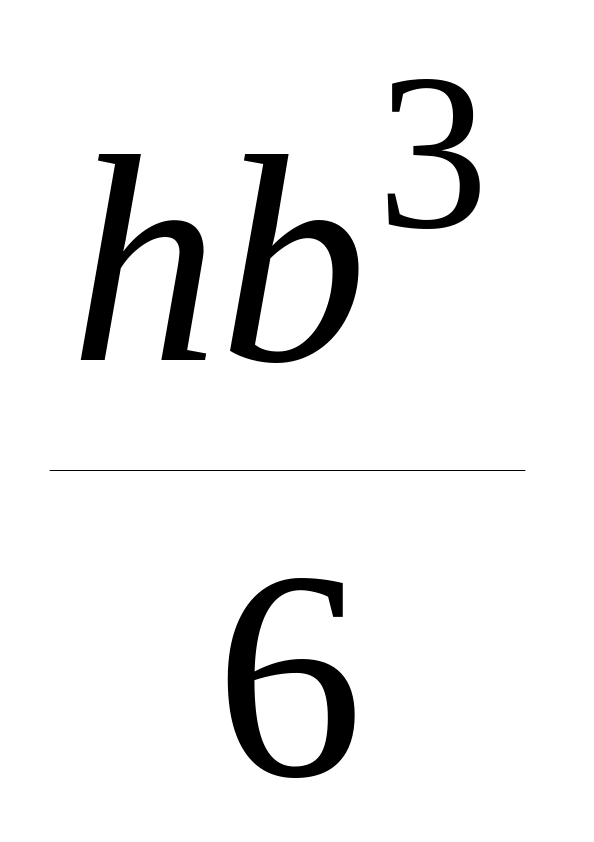
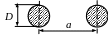
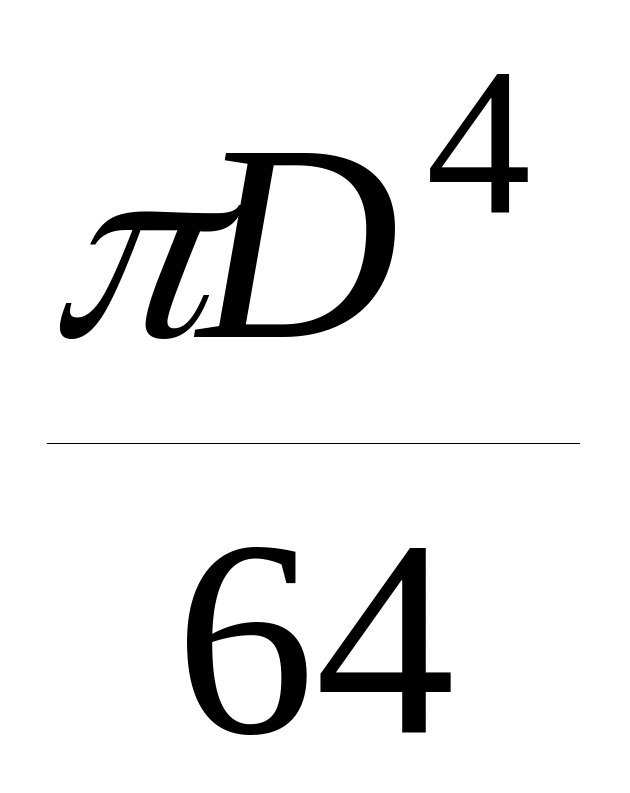
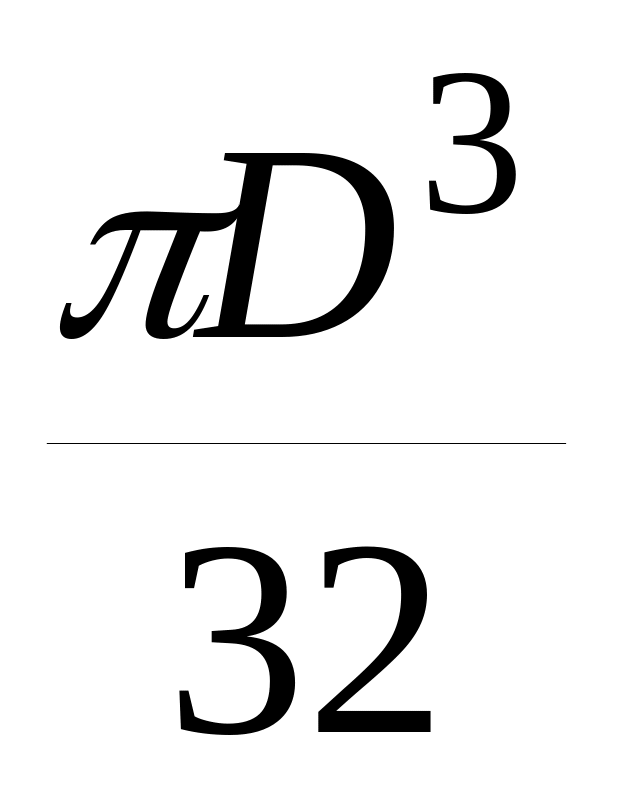
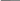
d a D