Ответы на вопросы

1. Световые волны и их основные характеристики. Световые лучи. Нормальная и лучевая скорости. Интенсивность света. Корпускулярно – волновой дуализм.

Волной называется процесс распространения колебаний или других возмущений в пространстве.

Электромагнитными волнами называется процесс распространения в пространстве переменных электрических и магнитных полей. Теоретически существование электромагнитных волн предсказано английским ученым Максвеллом в 1865 г., а впервые они экспериментально получены немецким ученым Герцем в 1888 г. Под светом будем понимать электромагнитное излучение в широком интервале длин волн .

В электромагнитной волне колеблются векторы Е и Н.

Как показывает опыт, физиологическое, фотохимическое, фотоэлектрическое и другие действия света вызываются колебаниями электрического вектора. В соответствии с этим мы будем в дальнейшем говорить о световом векторе.

Отношение скорости световой волны в вакууме к фазовой скорости v в некоторой среде называется абсолютным показателем преломления этой среды и обозначается буквой n.

N=

Для подавляющего большинства прозрачных веществ µ практически не отличается от единицы. Поэтому можно считать, что

N=

Формула связывает оптические свойства вещества с его электрическими свойствами. Значения показателя преломления характеризуют оптическую плотность среды. Среда с большим n называется оптически более плотной, чем среда с меньшим n. В веществе длины световых волн будут иными

ƛ0= ƛ=

Период и частота при переходе из среду в среду не изменяется. Частоты видимых световых волн лежат в пределах

Модуль среднего по времени значения плотности потока энергии, переносимой световой волной, носит название интенсивности света I. Плотность потока электромагнитной энергии определяется вектором Пойнтинга S. I~EH и E~H или I~EE.

Устройства предназначенные для обнаружения и измерения опт. Излучения называют опт.приёмниками. Линии, вдоль которых распространяется световая энергия, называются лучами. Усредненный вектор Пойнтинга (S) направлен в каждой точке по касательной к лучу. В изотропных средах направление (S) совпадает с нормалью к волновой поверхности, т. е. с направлением волнового вектора к. Следовательно, лучи перпендикулярны к волновым поверхностям. В анизотропных средах нормаль к волновой поверхности в общем случае не совпадает с направлением вектора Пойнтинга, так что лучи не ортогональны волновым поверхностям. Корпускуля́рно-волново́й дуали́зм — принцип, согласно которому любой объект может проявлять как волновые, так и корпускулярные свойства.курпускула-частица. свет можно трактовать как поток корпускул (фотонов), которые во многих физических эффектах проявляют свойства электромагнитных волн.

2. Центрированная оптическая система. Главные точки и плоскости. Формула оптической системы.

Оптической системой называется совокупность оптических деталей (призмы, линзы, зеркала), предназначенных для преобразования пучков световых лучей посредством преломления и отражения на поверхностях, которыми ограничены оптические детали.

Оптическую систему называют центрированной, если центры сферических поверхностей или оси симметрии других поверхностей, образующих оптическую систему, расположены на одной прямой, называемой оптической осью.

Совокупность лучей образует пучок. Если лучи при своем продолжении пересекаются в одной точке, пучок называется гомоцентрическим. Гомоцентрическому пучку лучей соответствует сферическая волновая поверхность. На рис. 1.1, а показан сходящийся, а на рис. 1.1,б — расходящийся гомоцентрический пучок ,в- параллельный.

Если пучок световых лучей, идущий из какой-либо точки Р (см.рис1), после прохождения через оптическую систему пересекается в точке Р', то точка Р' называется изображением точки Р. Изображение, образованное пересечением лучей выходящих из оптической системы, называют действительным, а изображение, образованное пересечением геометрических продолжений этих лучей - мнимым.

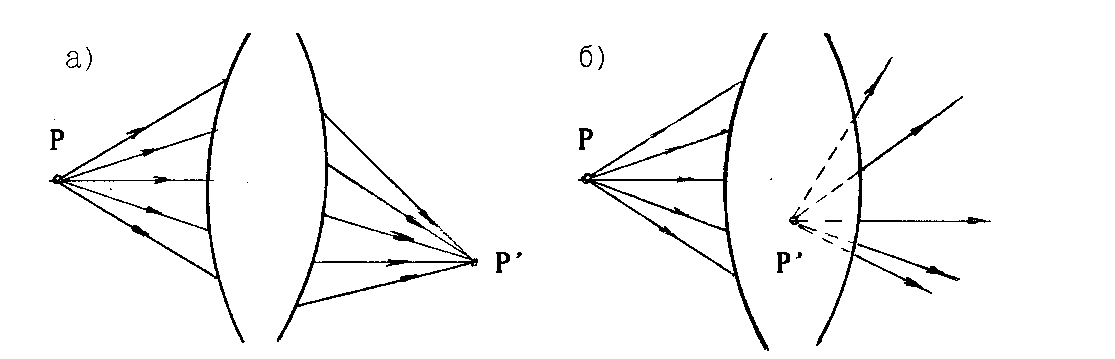
Рис.1. Изображение точки в оптической системе:

а - действительное, б - мнимое.

Идеальная оптическая система изображает точку в виде точки, т.е. все лучи, исходящие из любой точки предмета, собираются после выхода из системы в одной точке изображения. С помощью такой системы пространственная непрерывность точек Р отображается в виде пространственной непрерывности точек Р. Первая непрерывность точек называется пространством предметов, вторая — пространством изображений.

Каждой точке Р или плоскости S в пространстве предметов соответствует сопряженная с ней точка Р или плоскость S в пространстве изображений. Среди бесконечного множества сопряженных точек и сопряженных плоскостей имеются точки и плоскости, обладающие особыми свойствами.

Такие точки и плоскости называются кардинальными. К их числу относятся фокальные, главные и узловые точки и плоскости. Задание кардинальных точек или плоскостей полностью определяет свойства идеальной центрированной оптической системы.

Выберем в предметной плоскости Q перпендикулярной оптической оси отрезок длиной y. Его изображение будет расположено в сопряженной плоскости Q и будет иметь линейные размеры y ).

Отношение размера изображения к размеру предмета называют линейным увеличением оптической системы ():

 = У/ У. (3)

Для пары сопряженных плоскостей Q и Q' перпендикулярных оптической оси линейное

увеличение постоянно и не зависит от величины предмета. При  › 0 изображение перевернутое, при  ‹ 0  изображение прямое.

Две сопряженные и перпендикулярные оптической оси плоскости, в которых линейное увеличение равно плюс единице ( = +1), называются передней и задней главными плоскостями Qh и Qh Точки их пересечения с оптической осью называются главными точками Н и Н

Любой отрезок в передней главной плоскости изображается равным и одинаково расположенным отрезком в задней главной плоскости. Отсюда следует, что входящий в оптическую систему и выходящий из нее лучи,пересекают главные плоскости на равных высотах h = h.

Таким образом действие всех преломляющих поверхностей оптической системы для лучей, идущих из бесконечности, можно свести к действию плоскости, перпендикулярной оптической оси, содержащей в себе точку пересечения лучей входящих в эту систему и выходящих из нее. Для лучей, идущих слева направо, это будет задняя главная плоскость, а для лучей, идущих справа налево - передняя главная плоскость.

Положение фокусов и главных плоскостей определяют путем расчета или графического построения хода лучей, параллельных оптической оси, в прямом и обратном направлениях. При построениях изображений в оптической системе можно считать, что между главными плоскостями лучи идут параллельно оптической оси.

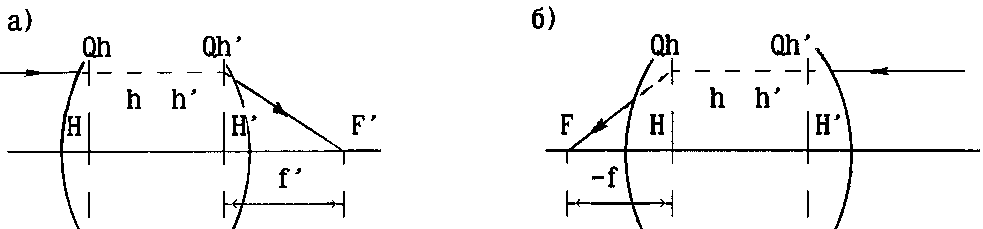
Задание кардинальных плоскостей или точек полностью определяет свойства оптической системы. В частности, зная положение кардинальных плоскостей, можно построить оптическое изображение, даваемое системой. Возьмем в пространстве предметов отрезок ОР, перпендикулярный к оптической оси. Положение этого отрезка можно задать либо расстоянием х отсчитанным от точки F до точки О, либо расстоянием s от Н до О.

Величины х и s, как и фокусные расстояния f и являются алгебраическими.

Проведем из точки Р луч 1 параллельный оптической оси. Он пересечет плоскость Н в точке А. В соответствии со свойствами главных плоскостей сопряженный лучу 1 луч Г должен проходить через сопряженную с точкой А точку А плоскости Н. Так как луч 1 параллелен оптической оси, сопряженный с ним луч 1’ пройдет через задний фокус F’. Теперь проведем из точки Р луч 2, проходящий через передний фокус F. Он пересечет плоскость Н в точке В.

Сопряженный с ним луч 2 пройдет через сопряженную с В точку В’ плоскости H’ и будет параллельным оптической оси. Точка Р’ пересечения лучей 1’ и 2’ представляет собой изображение точки Р. Изображение О’Р’, как и отрезок ОР, перпендикулярно к оптической оси.

Положение изображения О’Р’ можно охарактеризовать либо расстоянием х’ от точки F’ до точки О’, либо расстоянием s’ от Н’ до О’. Величины х’ и s’ являются алгебраическими. В случае, изображенном на рис. 116.7, они положительны.

Величина x’ определяющая положение изображения, закономерно связана с величиной х, определяющей положение предмета, и с фокусными расстояниями f и f’. Для прямоугольных треугольников с общей вершиной в точке F можно написать соотношение

Аналогично, для треугольников с общей вершиной в точке F’ имеем

Объединив оба соотношения, получим, что откуда

Это равенство называется формулой Ньютона.

. Из рис. видно, что (-x)=(-s)-(-f),x’=s’-f’/ Подставив эти выражения для в формулу и произведя преобразования, получим

При выполнении условия f’=-f формула упрощается следующим образом:

Соотношения представляют собой формулы центрированной оптической системы.