3.5. Емпірічна функція розподілу.

Нехай є статистичний розподіл частот деякої ознаки . Позначимо як загальну кількість спостережень. Нехай – довільне дійсне число (точка числової прямої). Позначимо як – кількість спостережень, при яких спостерігалися ознаки менше .

Тоді відносна частота події дорівнює . Якщо змінюється, т, взагалі кажучи, змінюється й , а отже й , тобто є функцією від . Ця функція знаходиться емпіричним (дослідним) шляхом, тому її називають емпіричною.

Означення. Емпірічною функцією розподілу називається функція , яка визначає для кожного значення відносну частоту події .

Тобто за означенням:

.

Означення. Інтегральну функцію розподілу генеральної сукупності називають теоретичною функцію розподілу.

Функція відрізняється від функції тим, що вона визначає ймовірність події , а функція – відносну частоту цієї події.

Якщо до функцій та застосувати теорему Бернуллі (див. п. 2.41), то отримаємо:

для будь якого . Тобто при збільшенні числа випробувань подія, яка полягає в тому, що емпірична функція розподілу буде мало відрізнятися від теоретичної функції розподілу, стає практично достовірною. А звідси випливає доцільність використання функції для наближеного зображення теоретичної функції розподілу генеральної сукупності. Можна сказати, що функція є статистичним аналогом функції .

Такий висновок підтверджується також тим, що функція має властивості, які аналогічні властивостям функції . А саме.

1. Всі значення функції належать відрізку :

.

2. Функція є неспадною, тобто, якщо , то .

3. .

Ця властивість фактично означає наступне: якщо – найменша варіанта,

то при ; якщо – найбільша варіанта, то при .

Приклад. Знайти емпіричну функцію розподілу за даним статистичним розподілом вибірки:

	2	6	10
	12	18	30

Побудувати графік функції .

Об’єм вибірки дорівнює . Найменша варіанта , отже при . Найбільша варіанта , отже при . Знайдемо при . Подія у цьому випадку еквівалента події , а відносна частота цієї події , тобто . При подія еквівалента сумі подій , , і відносна частота цієї суми , тобто . Отже дістаємо:

Графік цієї функції має вигляд:

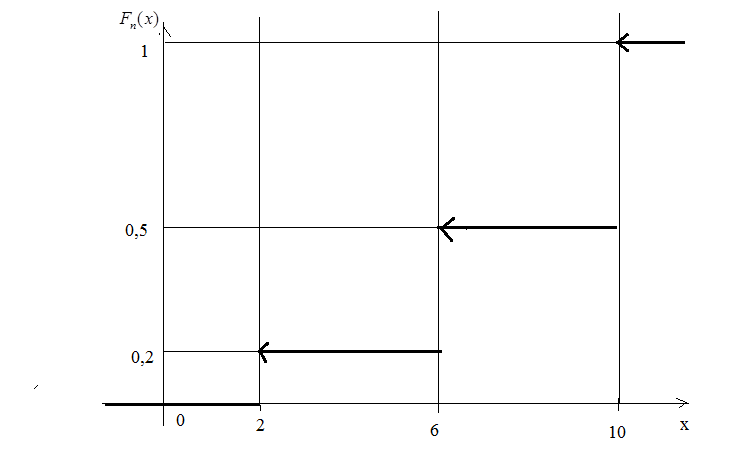
Рис. 40.

Цей графік можна розглядати як наближений графік теоретичної функції розподілу. Він демонструє перелічені вище властивості функції , а також наступні властивості: ця функція кусково-стала, у точках, що відповідають значенням ознаки, вона має розриви I роду і неперервна зліва в цих точках. Легко помітити, що ці властивості аналогічні властивостям функції розподілу дискретної випадкової величини (див. п. 2.16).

6. . Полігон і гістограма

З метою наглядного відображення даних вибірки використовуються графічні засоби. До них, зокрема, відносяться полігон і гістограма.

Нехай задано вибірку:

– об’єм вибірки.

Означення. Полігоном частот вибірки називається ламана лінія на координатній площині, вершини якої знаходяться у точках , , … , .

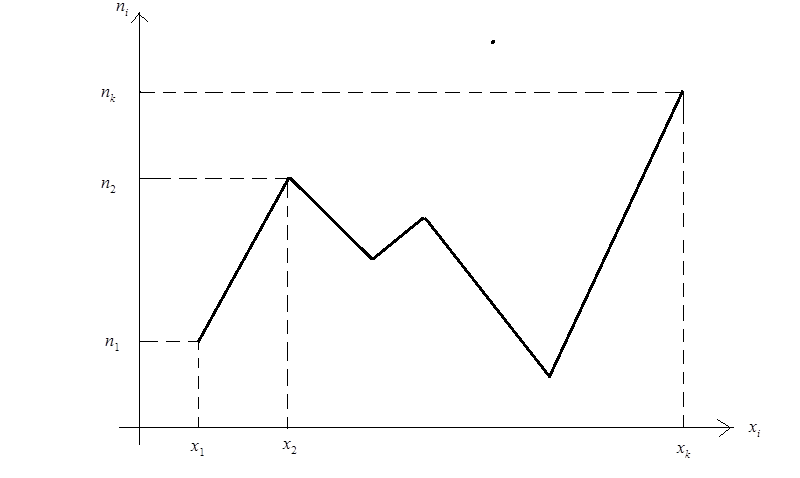
Рис. 41.

Означення. Полігоном відносних частот вибірки називається ламана лінія на координатній площині, вершини якої знаходяться у точках , , … , , де – відносні частоти вибірки.

Приклад. Нехай задано вибірку:

	1	2	4	6	7
	10	20	15	5	30

Побудувати полігони частот та відносних частот.

Полігон частот має вигляд:

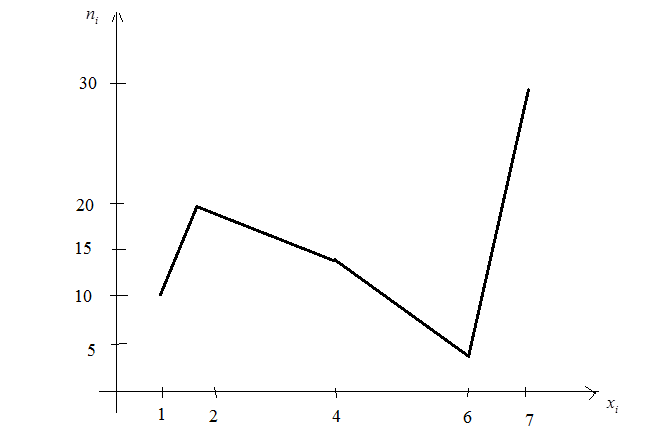
Рис. 42.

Знайдемо відносні частоти:

,

, , , , .

Статистичний розподіл відносних частот:

	1	2	4	6	7
	0,125	0,25	0,1875	0,0625	0,375

Полігон відносних частот має вигляд:

Рис. 43.

Якщо ознака неперервна, або число різних елементів вибірки досить велике, то замість полігону використовують гістограму. Будується вона наступним чином. Розглянемо деякий інтервал , до якого належать всі елементи вибірки. Розіб’ємо цей інтервал на частинних проміжків. Для спрощення будемо вважати, що всі ці проміжки мають однакову довжину , хоча у загальному випадку довжини цих проміжків можуть бути різними. Для кожного частинного проміжку знайдемо суму частот тих елементів вибірки, які потрапили до цього проміжку. Позначимо як – суму частот елементів вибірки, які потрапили до -го проміжку . Тоді . На кожному частинному проміжку побудуємо прямокутника, основа якого співпадає з частинним проміжком, а висота дорівнює , де – номер проміжку. Висоти прямокутників таким чином пропорційні кількості елементів вибірки, які потрапили у відповідний проміжок – чим більше елементів потрапило у частинний проміжок, тим вище прямокутник, побудований на цьому проміжку. Тобто ці висоти відображають щільність вмісту елементів вибірки у відповідному проміжку.

Сукупність цих прямокутників є ступінчатою фігурою, яка й називається гістограмою.

Площа -го прямокутника дорівнює , тобто кількості елементів, що потрапили до -го проміжку. Таким чином площа всієї гістограми дорівнює об’єму вибірки.

Іноді будують гістограму відносних частот. Вона відрізняється тим, що висота -го прямокутника дорівнює . Таким чином його площа , а площа всієї гістограми:

.

Гістограма таким чином є статистичним аналогом щільності розподілу випадкової величини, її контур наближено відображає графік відповідної щільності розподілу. Наприклад, якщо висоти прямокутників приблизно однакові, то це свідчить про те, що розподіл відповідної випадкової величини близький до рівномірного (див. п. 2.21).

Рис. 44.

Якщо висоти прямокутників помітно спадають з ростом номеру частинного проміжку, то це свідчить про те, що розподіл відповідної випадкової величини близький до показникового (див. п. 2.22).

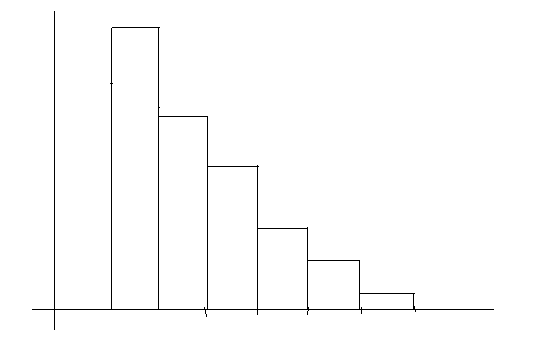
Рис. 45.

Якщо висоти прямокутників, які знаходяться ближче до середини інтервалу , помітно більше, ніж висоти прямокутників, що знаходяться ближче до кінців інтервалу , то це свідчить про те, що розподіл близький до нормального (див. п. 2.25).

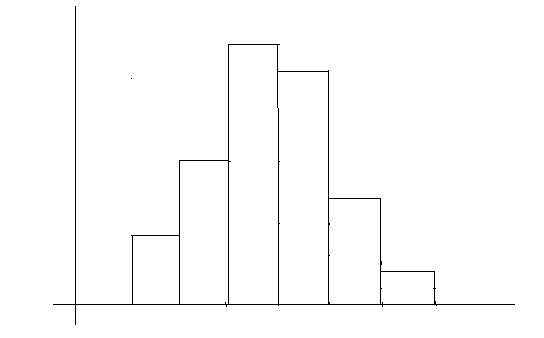
Рис. 46.

Приклад. Нехай відомо наступний розподіл частот вибірки:

Частинні проміжки ( )	Сума частот вибірки	Щільність частот
5 – 10	4	0,8
10 – 15	6	1,2
15 – 20	16	3,2
20 – 25	36	7,2
25 –30	24	4,8
30 – 35	10	2,0
35 – 40	4	0,8

Гістограма має вигляд:

Рис. 47.

Форма гістограми свідчить про те, що даний розподіл близький до нормального.