3.23. Вибірковий коефіцієнт кореляції.

Перетворимо формули для і наступним чином:

.

Величина

називається вибірковим коефіцієнтом кореляції. З використанням його отримаємо:

.

Аналогічно дістанемо:

.

Підставимо ці значення у рівняння прямої лінії регресії :

.

Або:

. (*)

Рівняння (*) називається вибірковим рівнянням прямої лінії регресії на .

Аналогічно знаходиться вибіркове рівняння прямої лінії регресії на :

. (**)

На площині обидві прямі (*) та (**) проходять через одну й ту ж точку , яка називається центром сумісного розподілу.

Вибірковий коефіцієнт кореляції характеризує тісноту зв’язку між величинами та . Нескладно довести, що . Чим ближче до 1, тим тісніше зв’язок між та . У цьому випадку рівняння (*) буде близьким до рівняння (**) (у випадку ці рівняння співпадають), тобто прямі лінії регресії, що описуються цими рівняннями, будуть відрізнятися незначно, кут між ними буде невеликим. Дійсно, тангенс цього кута виражається величиною:

, звідки видно, що у випадку буде , тобто або .

Для задач геології зв’язок між величинами вважається суттєвим, якщо .

3.24. Приклад побудови прямих ліній регресії.

Нехай величини та приймають значення:

	-7,00	-6,00	-5,00	-4,00	-3,00	-2,00	-1,00	0,00	1,00
	7,75	6,27	5,67	4,26	3,09	2,03	1,32	0,79	-0,70

Треба знайти вибірковий коефіцієнт кореляції, визначити тісноту зв’язку між величинами та , побудувати рівняння прямих ліній регресії на та на , побудувати ці прямі на координатній площині.

Для знаходження вибіркового коефіцієнта кореляції скористаємось формулою:

.

Знайдемо:

, , , , , , ,

, .

Отже:

.

Ми бачимо, що досить близький до 1, отже зв’язок між величинами та значний.

Рівняння прямої лінії регресії на :

.

Підставляючи знайдені величини, отримаємо:

.

Або:

.

Або:

.

Рівняння прямої лінії регресії на :

.

Підставляючи знайдені величини, отримаємо:

.

Або:

.

Або:

.

Ми бачимо, що кутові коефіцієнти цих прямих майже співпадають, і обидві ці прямі проходять через точку (-3; 3,39) – центр сумісного розподілу. Отже ці прямі також майже співпадають, що також свідчить про тісний зв’язок між величинами та .

Прямі лінії регресії на та на побудовано на рис. 49.

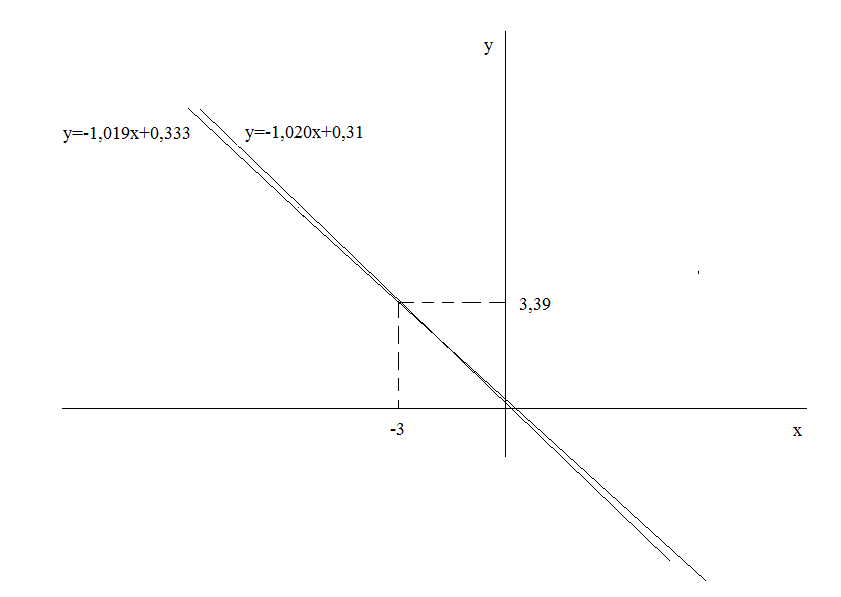
Рис. 49.

Контрольні питання до розділу III.

1. У чому полягає предмет математичної статистики, які її основні задачі?

2. Що є основним методом математичної статистики?

3. Що таке генеральна та вибіркова сукупності?

4. Що таке повторна та безповторна вибірка?

5. Які існують способи відбору з генеральної сукупності?

6. Що таке статистичний розподіл вибірки? Які у нього спільні риси із законом розподілу дискретної випадкової величини?

7. Що таке емпірична функція розподілу? Які у неї спільні риси з функцією розподілу випадкової величини?

8. Що таке полігон і гістограма? Як будується гістограма? Що є аналогом гістограми в теорії випадкових величин?

9. Що таке точкові оцінки параметрів розподілів, які існують вимоги до них?

10. Що таке вибіркове середнє та вибіркова дисперсія? Аналогом яких характеристик випадкових величин є ці числові характеристики вибірки?

11. Що таке початкові та центральні емпіричні моменти?

12. У чому полягає метод моментів точкових оцінок параметрів розподілів?

13. У чому полягає метод найбільшої правдоподібності точкових оцінок параметрів розподілів?

14. Що таке мода, медіана, розмах вар’ювання?

15. У чому полягає ідея інтервальних оцінок параметрів розподілів? У яких випадках доцільніше використання точкових оцінок, а у яких – інтервальних?

16. Що таке довірчий інтервал і довірча ймовірність?

17. Як будується довірчий інтервал для оцінки математичного сподівання нормального розподілу?

18. Що таке статистична гіпотеза?

19. Що таке критерій узгодженості? Які бувають критерії узгодженості? Як ними користуються на практиці?

20. Що таке функціональна, статистична та кореляційна залежності? Наведіть відповідні приклади.

21. Що таке вибірковий коефіцієнт кореляції, що він характеризує?

22. У чому полягає ідея методу найменших квадратів побудови прямих ліній регресії?

Вправи для самостійного розв’язування.

1. Знайти емпіричну функцію заданого статистичного розподілу та побудувати її графік.

	15	20	25	30
	10	15	30	20

2. Побудувати полігон частот та відносних частот заданого розподілу вибірки

	4	7	8	12	15	20
	12	2	8	8	7	3

3. Побудувати гістограму частот за заданим розподілом вибірки:

Частинні проміжки ( )	Сума частот вибірки	Щільність частот
1 – 5	10	2,5
5 – 9	20	5
9 – 13	50	12,5
13 – 17	12	3
17 –21	8	2

4. З генеральної сукупності добуто вибірку:

	1	3	6	26
	8	40	10	2

Знайти незсунуту оцінку середнього генерального.

5. Знайти вибіркову дисперсію та вибіркове середньоквадратичне відхилення за даним розподілом вибірки:

	2502	2804	2903	3028
	8	30	6	2

6. Знайти вибіркову дисперсію та вибіркове середньоквадратичне відхилення за даним розподілом вибірки:

	18,4	18,9	19,3	19,6
	5	10	20	15

7. Знайти виправлену вибіркову дисперсію за даним розподілом вибірки:

	0,01	0,05	0,09
	2	3	5

8. Вибірка з великої партії електроламп містить 100 ламп. Середня тривалість горіння однієї лампи 1000 годин. Знайти з надійністю довірчий інтервал для середньої тривалості горіння всієї партії, якщо відомо, що середньоквадратичне відхилення тривалості горіння лампи 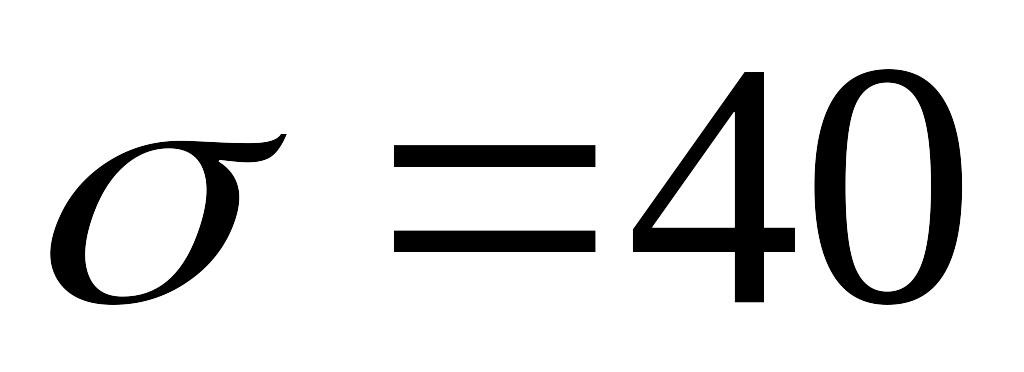годин.

9. З генеральної сукупності добуто вибірку:

	-2	1	2	3	4	5
	2	1	2	2	2	1

З надійністю знайти довірчий інтервал для оцінки математичного сподівання нормально розподіленої ознаки генеральної сукупності.

10. З генеральної сукупності добуто вибірку:

	-0,5	-0,4	-0,2	0	0,2	0,6	0,8	1	1,2	1,5
	1	2	1	1	1	1	1	1	2	1

З надійністю знайти довірчий інтервал для оцінки середньоквадратичного відхилення нормально розподіленої ознаки генеральної сукупності.

11. За допомогою критерія Пірсона на рівні значущості 0,05 перевірити гіпотезу про нормальний розподіл генеральної сукупності, якщо з неї добуто вибірку:

	5	7	9	11	13	15	17	19	21
	15	26	25	30	26	21	24	20	13