3.19. Критерій Пірсона перевірки статистичної гіпотези про нормальний розподіл випадкової величини.

При отриманні критерію для перевірки гіпотези, яка полягає в тому, що функцією розподілу випадкової величини є певна функція , ми вводимо міру відхилення емпіричної функції розподілу від гіпотетичної функції розподілу . В якості такої міри часто використовується міра, яку введено К. Пірсоном.

Нехай задано вибірку об’єма . Оберемо деякий інтервал , у якому містяться всі елементи вибірки. Розіб’ємо цей інтервал на декілька частин (для спрощення вважатимемо їх рівними). Позначимо , ( – число інтервалів). Частинні проміжки позначатимемо як , ,…, ,…, .

Припустимо, що випадкова величина , що досліджується, розподілена нормально із параметрами і . Тоді (див. п. 2.26):

.

Оскільки параметри та завчасно невідомі, то їх наближено можна замінити їх статистичними аналогами, відповідно та . Тоді:

.

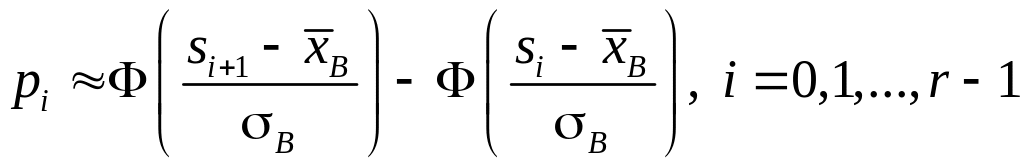Знаючи ймовірності , знайдемо для кожного частинного проміжку величину . Величини називаються теоретичними частотами – вони показують, скільки елементів вибірки, скоріше всього, потрапило б до відповідного інтервалу, якби випадкова величина дійсно була б розподілена нормально з параметрами та .

Далі для кожного частинного проміжку знайдемо величину , яка показує, скільки дійсно елементів вибірки потрапило до цього частинного проміжку. Величини називаються емпіричними частотами. Якщо гіпотеза про нормальний розподіл правдоподібна, то емпіричні частоти не повинні значно відрізнятися від теоретичних частот, тобто має бути: . Тому треба ввести до розгляду величину, яка характеризувала б ступінь близькості цих частот. За пропозицією К. Пірсона такою мірою є:

.

Це й є міра відхилення емпіричної функції розподілу від теоретичної. Користуються цією мірою наступним чином. Визначається так зване число ступенів вільності ( – кількість частинних проміжків). Задається рівень значущості , і в залежності від і за спеціальною таблицею (див. Додаток ) визначають критичну точку . Якщо знайдена за даними вибірки величина більше, ніж , то це буде означати, що розбіжність між емпіричними та теоретичними частотами суттєве, і у цьому випадку гіпотеза про нормальний розподіл має бути відкинута. Якщо , то це означає, що суттєвої розбіжності між емпіричними та теоретичними частотами нема, і тому гіпотеза може бути прийнята.

3.20. Приклад перевірки статистичної гіпотези про нормальний розподіл випадкової величини за допомогою критерію Пірсона.

Нехай за допомогою критерію Пірсона на рівні значущості треба перевірити гіпотезу про нормальний розподіл випадкової величини за даними наступної вибірки об’єму :

0,60 1,64 2,07 2,20 2,31 2,81 2,82 2,91 3,41 3,42

3,54 3,77 3,90 4,23 4,33 4,34 4,57 5,08 5,15 5,49

5,50 5,51 5,64 5,66 5,77 5,96 6,08 6,09 6,13 6,16

6,31 6,38 6,39 6,59 6,68 7,18 7,41 7,44 7,72 8,12

8,29 8,42 8,55 8,87 8,93 9,24 9,52 9,56 10,07 10,72

Знайдемо числові характеристики цієї вибірки:

, , , , .

У припущенні, що випадкова величина розподілена нормально, знайдемо з надійністю довірчі інтервали для оцінки математичного сподівання та середньоквадратичного відхилення випадкової величини. Довірчий інтервал для оцінки математичного сподівання знаходимо за формулою (***) п. 3.17, де значення параметра для , дорівнює: . Підставивши до цієї формули числові дані, отримуємо:

.

Довірчий інтервал для оцінки середньоквадратичного відхилення знаходимо за формулою (****) п. 3.17, де значення параметра для , дорівнює: . Підставивши числові дані, отримуємо:

(1,90; 2,92).

Перейдемо тепер до перевірки статистичної гіпотези про нормальний розподіл. Оберемо відрізок , до якого входять всі елементи вибірки, і розіб’ємо його на 6 частинних проміжків довжиною : , , , , , . Для кожного проміжку знайдемо ймовірність, що випадкова величина прийме значення з цього проміжку, за формулою:

.

Маємо:

,

,

,

,

,

.

Тепер для кожного частинного проміжку знайдемо теоретичні частоти :

,

,

,

,

,

.

Далі для кожного частинного проміжку знайдемо емпіричні частоти , тобто підрахуємо, скільки елементів вибірки потрапило до цього частинного проміжку. Отримаємо:

, , , , , .

Зведемо отримані дані до наступної таблиці:

Частинні проміжки	Емпірічні частоти	Ймовірності	Теоретичні частоти
	2	0,0483	2,42	0,1764	0,073
	11	0,1707	8,53	6,1	0,715
	13	0,3093	15,46	6,05	0,391
	13	0,2879	14,39	1,93	0,134
	9	0,1378	6,89	4,45	0,646
	2	0,0337	1,68	0,01	0,06

Обчислимо суму елементів останнього стовпця таблиці, тобто

.

Порівняємо це значення з критичною точкою , яка знаходиться за таблицею (див. Додаток, Таблиця 5) для числа ступенів вільності та рівня значущості : . Оскільки , то гіпотеза про нормальний розподіл випадкової величини приймається.

За першими двома стовпцями наведеної таблиці нескладно побудувати гістограму частот вибірки:

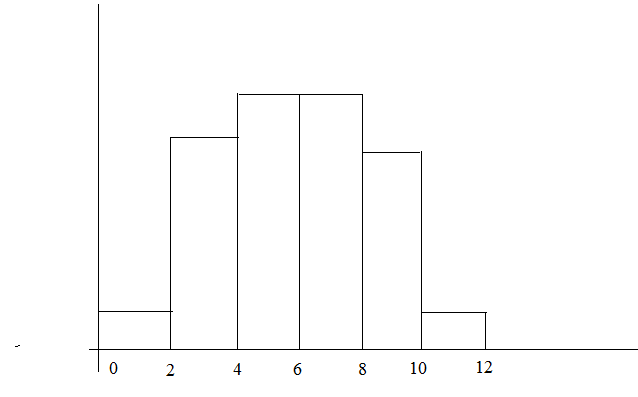
Рис. 48.

Вигляд гістограми також демонструє правдоподібність гіпотези про нормальний розподіл.