2.14. Неперервні випадкові величини. Функція розподілу.

Перейдемо тепер до розгляду неперервних випадкових величин (НВВ). Знову виникає питання – як таку величину можна охарактеризувати? Зрозуміло, що задати перелік всіх її можливих значень, як ми це робили для дискретних випадкових величин, тепер неможливо. Адже неможливо перелічити всі дійсні числа з суцільного проміжку. Тому виникає необхідність надання загального способу опису випадкових величин будь яких типів. Таким способом є введення так званої функції розподілу випадкової величини.

Нехай – дійсне число, – випадкова величина. При проведенні випробувань величина може з певною ймовірністю прийняти значення, яке менше . Очевидно, що, якщо змінюється, то, взагалі кажучи, буде змінюватися й ця ймовірність, тобто ця ймовірність є функцією . Ця функція називається функцією розподілу випадкової величини .

Означення. Функцією розподілу випадкової величини називається функція , яка дорівнює ймовірності того, що внаслідок випробування випадкова величина прийме значення, менше, ніж :

.

З геометричної точки зору функція є ймовірність того, що випадкова величина внаслідок випробування прийме значення, яке на числовій прямій зображується точкою, що лежить зліва від точки , тобто потрапить до інтервалу (рис. 16).

Рис. 16.

Приклад. Нехай точка випадковим чином потрапляє в круг радіусу . Нехай – випадкова величина, яка дорівнює відстані від точки до центра круга (рис. 17). Побудувати функцію розподілу величини .

Нехай – довільне дійсне число. Для кожного значення нам треба знайти . Розглянемо три можливі випадки.

1). . Тоді, оскільки – це за умовою задачі відстань, яка не може бути від’ємною, подія неможлива, отже .

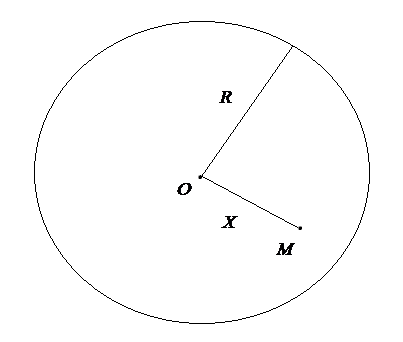
Рис. 17.

2). . Тоді є ймовірністю того, що точка , потрапляючи в круг радіусу , потрапить при цьому в концентричний з ним менший (принаймні, не більший) круг радіусу . Згідно з формулою геометричної ймовірності (див. п. 1.7):

.

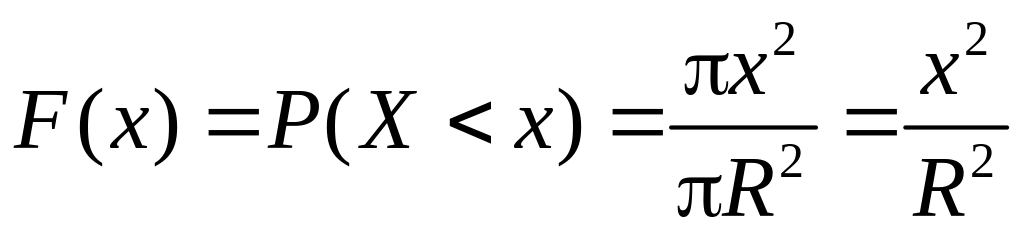3). . Тоді є ймовірністю того, що точка , потрапляючи в круг радіусу , потрапить в концентричний з ним більший круг радіусу . А це трапиться обов’язково, тобто подія цього разу достовірна, тому .

Таким чином маємо:

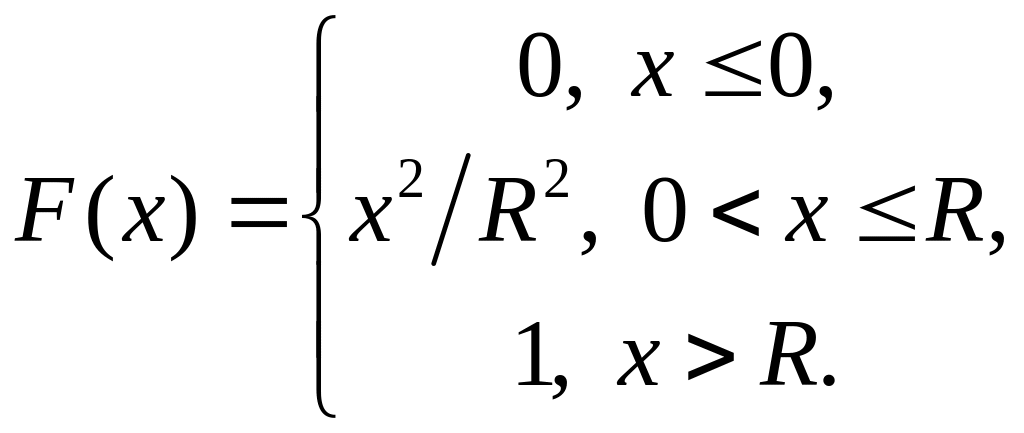
Графік функції наведено на рис. 18.

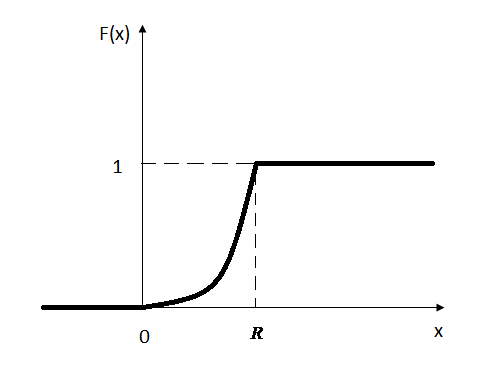
Рис. 18.

2.15. Властивості функції розподілу.

Властивість 1. Значення функції розподілу належать відрізку :

.

Дійсно, за означенням функція розподілу є ймовірність, а ймовірність завжди є число з відрізку .

Властивість 2. Функція є неспадною, тобто, якщо , то .

Доведення. Розглянемо:

, оскільки (будь яка ймовірність є невід’ємним числом).

Водночас отримуємо рівність:

. (*)

Якщо випадкова величина неперервна, то можна показати, що її функція розподілу також неперервна, тобто

.

Цей факт можна проілюструвати на підставі рівності (*). Покладемо у цій рівності , . Дістанемо:

. (**)

Ймовірність у лівій частині цієї рівності є ймовірність потрапляння випадкової точки (значення НВВ ) в інтервал, довжина якого дорівнює . І якщо прямує до нуля, то на підставі формули геометричної ймовірності ймовірність також прямує до нуля, отже

, а це й означає неперервність функції .

Властивість 3. Ймовірність того, що НВВ прийме одне певне значення, дорівнює нулю.

Ця властивість безпосередньо випливає з рівності:

.

Наслідок. Для НВВ мають місце рівності:

.

Дійсно, розглянемо, наприклад:

.

Властивість 3 цікава, і може мати невірне тлумачення. З цієї властивості, здавалось би, випливає, що подія неможлива, адже її ймовірність дорівнює нулю. І внаслідок довільності звідси випливав би парадоксальний висновок, що НВВ не може прийняти ніякого певного значення. В той же час очевидно, що внаслідок випробування випадкова величина обов’язково прийме деяке певне значення. Отже ми бачимо, що з того, що ймовірність події дорівнює нулю, не випливає, взагалі кажучи, що ця подія неможлива. Глибокі причини цього факту розкриваються в більш детальних курсах теорії ймовірностей, які ґрунтуються на теорії міри та теорії функцій дійсного змінного.

Властивість 4. Якщо всі можливі значення випадкової величини належать інтервалу , то при і при .

Доведення. Нехай . Тоді подія неможлива (значень, менших , величина не приймає), отже .

Нехай . Тоді подія достовірна (всі можливі значення величини менше ), отже .

Властивість 5. Справедливі наступні співвідношення:

, .

Доведення. Дійсно, розглянемо:

(значень, менших , зрозуміло, не існує).

(всі можливі значення випадкової величини менше ).

Приклади.

1. Функція розподілу НВВ задається рівністю:

, .

Визначити сталі і і знайти .

Маємо:

,

.

Отже для сталих і отримали систему двох лінійних алгебраїчних рівнянь:

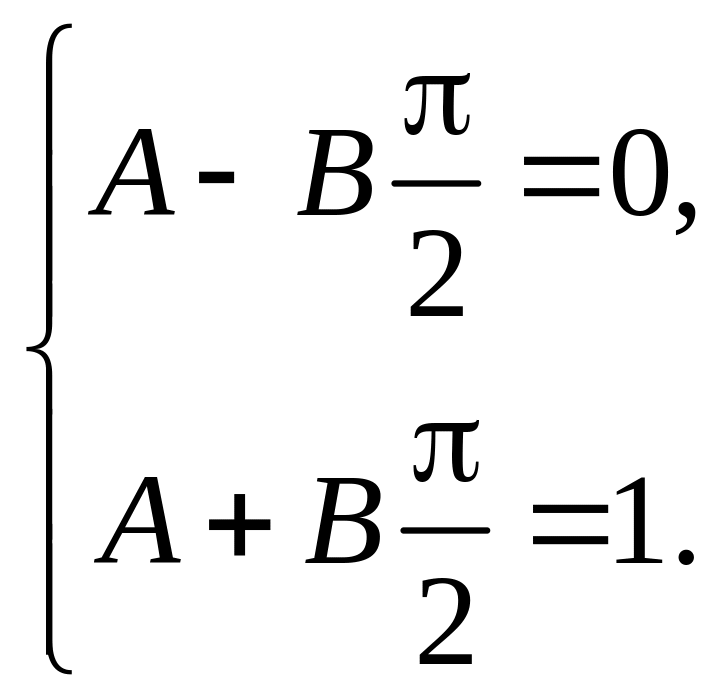
Розв’язуючи цю систему, отримуємо:

.

Отже

.

Графік цієї функції зображено на рис. 19.

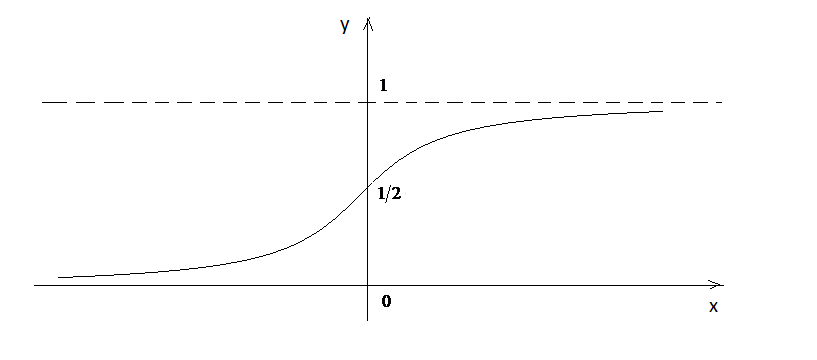
Рис. 19.

Знайдемо тепер:

.

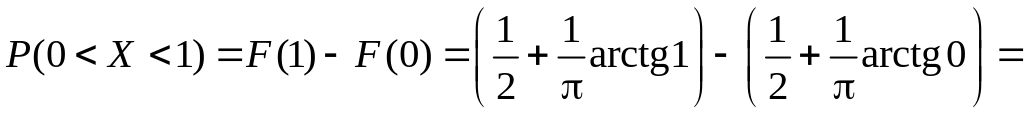
2. НВВ задана своєю функцією розподілу:

Визначити сталі і і знайти ймовірність того, що внаслідок 4-х незалежних випробувань величина рівно 3 рази прийме значення, яке належить інтервалу .

Сталі і визначимо з умови неперервності функції , зокрема, у точках та . Границі справа та зліва функції в цих точках мають збігатися, отже

.

Таким чином отримали систему лінійних алгебраїчних рівнянь:

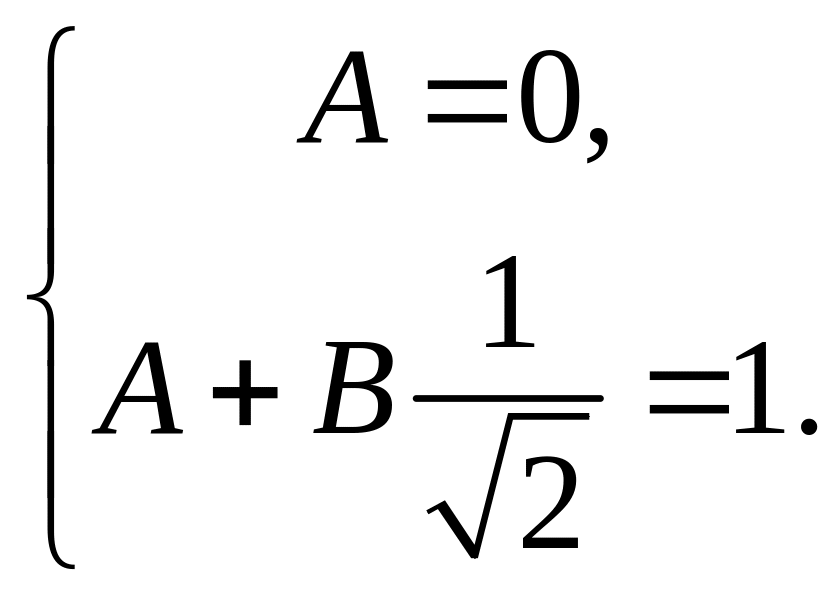
Звідси отримуємо: . Отже:

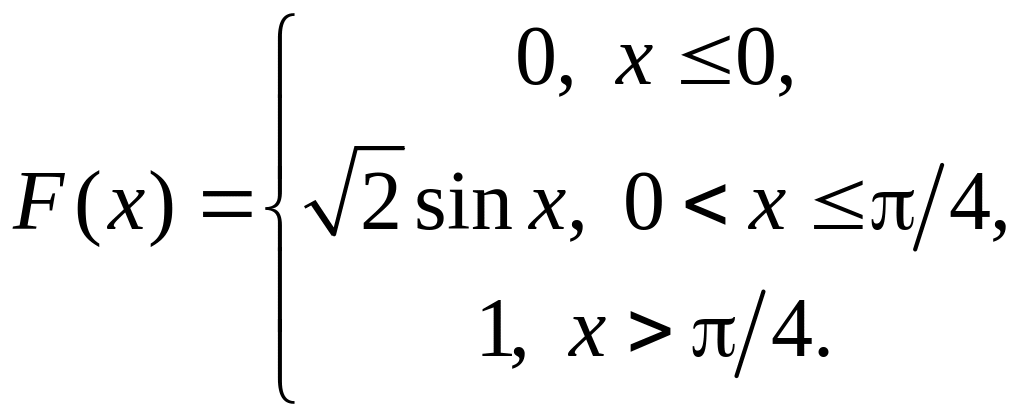
Знайдемо тепер:

.

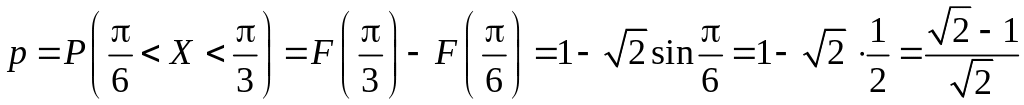Ймовірність того, що внаслідок 4-х випробувань значення з інтервалу випадкова величина прийме рівно 3 рази, знайдемо за формулою Бернуллі (див. п. 1.13):

.
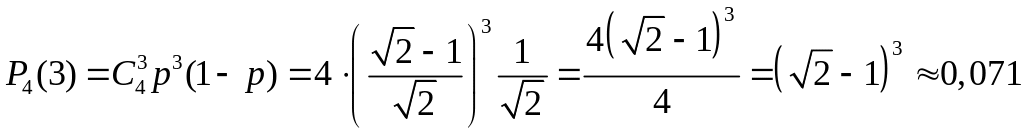