2.12. Розподіл Пуассона.

Означення. ДВВ називається розподіленою за законом Пуассона з параметром , якщо вона може приймати значення , причому

.

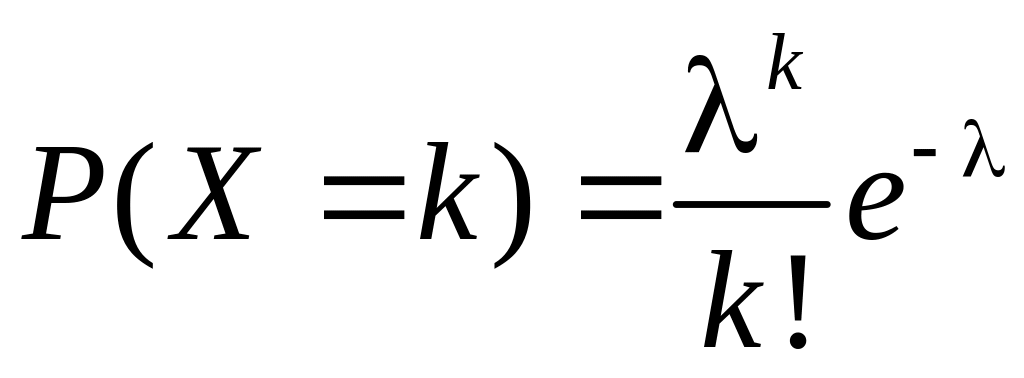Тобто закон розподілу має вигляд:

	0	1	2

.

Ця величина може приймати зліченну множину значень. Розподіл Пуассона іноді називають розподілом рідких подій. Прикладами випадкових величин, розподілених за цим законом можуть бути: число нещасних випадків, число дефектів у виробничих процесах тощо. Цей розподіл використовується у задачах статистичного контролю якості, в теорії надійності, теорії масового обслуговування та інших галузях.

Якщо у схемі незалежних випробувань число випробувань досить велике, а ймовірність появи події в одному випробуванні прямує до нуля, то біноміальний розподіл є близьким до розподілу Пуассона, параметр якого (див. п. 1.14).

Перевіримо виконання умови нормування. Розглянемо:

.

Знайдемо тепер математичне сподівання розподілу Пуассона:

.

Отже математичне сподівання розподілу Пуассона дорівнює параметру .

Знайдемо тепер дисперсію. Для цього спочатку знайдемо математичне сподівання квадрату випадкової величини:

.

Звідси маємо:

.

Таким чином, дисперсія розподілу Пуассона співпадає з математичним сподіванням і також дорівнює параметру . Очевидно тоді, що середньоквадратичне відхилення

.

Приклад. Прилад складається з великого числа незалежно працюючих елементів з однаковою дуже малою ймовірністю відмови кожного елементу за час . Знайти середнє число елементів, що відмовили за час , якщо ймовірність того, що за цей час відмовить хоча б один елемент, дорівнює 0,98.

Оскільки число елементів велике, елементи працюють незалежно один від одного, а ймовірність відмови кожного елемента мала, то число відмовлень розподілено за законом Пуассона. І треба знайти параметр – середнє число відмовлень.

Ймовірність того, що відмовить хоча б один елемент, дорівнює (див. п. 1.14):

,

отже

, звідки

.

Тоді

.

Отже за час відмовить у середньому 4 елементи.

2.13. Геометричний розподіл.

Означення. ДВВ називається розподіленою за геометричним законом з параметром , якщо вона може приймати значення , причому , де .

Тобто закон розподілу має вигляд:

	1	2	3

Припустимо, що ймовірність появи події в одному випробуванні дорівнює . Скільки треба провести випробувань до першої появи події ? Число цих випробувань й є випадкова величина , яка розподілена за геометричним законом. Очевидно, що вона може приймати зліченну множину значень: теоретично можна нескінченно продовжувати випробування, доки подія з’явиться.

Перевіримо виконання умови нормування. Знайдемо:

.

Тут ми скористалися формулою суми нескінченно спадної геометричної прогресії (звідси й назва розподілу) з першим членом і знаменником .

Знайдемо тепер математичне сподівання:

.

Тут ми скористалися тим, що степеневий ряд на інтервалі його збіжності можна почленно диференціювати.

Таким чином середнє число випробувань до першої появи події обернено пропорційно ймовірності цієї події.

Знайдемо дисперсію:

.

Розглянемо спочатку:

.

Тепер з виразу для дисперсії маємо:

.

Тоді середньоквадратичне відхилення:

.

Приклад. Скільки в середньому треба провести пострілів до цілі, якщо кожне влучання відбувається з ймовірністю 0,02?

Скористаємось геометричним розподілом. Середнє число випробувань (математичне сподівання) для нього дорівнює , отже

.

Тобто в середньому треба 50 пострілів.