2.10. Початкові та центральні теоретичні моменти.

Розглянемо ДВВ , яку задано наступним законом розподілу:

	1	2	5
	0,6	0,2	0,2

Її математичне сподівання:

.

А тепер розглянемо іншу ДВВ , яка, порівняно з величиною , має ще одне можливе значення, яке значно більше значень величини :

	1	2	5	100
	0,6	0,2	0,19	0,01

Ймовірність цього значення 100 дуже мала. Тобто при випробуваннях таке значення приймається випадковою величиною дуже рідко. Знайдемо:

.

Ми бачимо, що, незважаючи на появу у величини нового значення 100, яке значно більше решти значень, математичне сподівання величини , порівняно з математичним сподіванням величини , змінилося далеко не так значно. Тобто це велике значення 100 у математичному сподівання величини практично не урахувалося – число за своїм порядком таке ж саме, як і число . Це пов’язано з тим, що ймовірність значення 100 дуже мала.

Розглянемо тепер

.

А ось це число вже значно більше, ніж , і за своїм порядком воно таке ж саме, як це рідке значення 100. Тобто число дозволяє краще урахувати вплив на математичне сподівання того можливого значення, яке велике, але має малу ймовірність. Тому доцільно розглядати математичне сподівання натурального степеня випадкової величини.

Означення. Початковим моментом порядку випадкової величини називається математичне сподівання величини :

.

Зокрема:

.

З використанням початкових моментів формулу (*) п. 2.7 для обчислення дисперсії можна записати так:

.

Означення. Центральним моментом порядку випадкової величини називається математичне сподівання величини :

.

Зокрема:

,

.

Таким чином маємо:

.

Нескладно довести також справедливість наступних формул:

,

.

Моменти вищих порядків використовуються рідко.

Приклад. ДВВ задано законом розподілу:

	3	5
	0,2	0,8

Знайти центральні моменти 1-го, 2-го, 3-го та 4-го порядків.

Знайдемо спочатку початкові моменти 1-го, 2-го, 3-го та 4-го порядків:

;

;

;

.

Тепер знайдемо центральні моменти:

;

;

;

.

2.11 Біноміальний розподіл.

У цьому та двох наступних параграфах ми познайомимось з деякими законами розподілів дискретних випадкових величин, які зустрічаються в прикладних задачах. Тут ми розглянемо так званий біноміальний розподіл.

Означення. ДВВ називається розподіленою за біноміальним законом з параметром , якщо вона приймає значення ( – натуральне число), причому .

Тобто закон розподілу величини має вигляд:

	0	1	2

.

Легко помітити, що ДВВ – число появ у випробуваннях події за умови, що ймовірність появи події у одному випробуванні дорівнює . Та ймовірність того, що подія з’явиться разів, тобто , обчислюється за формулою Бернуллі (див. п. 1.13). Біноміально розподілені величини досить поширені на практиці. Зокрема вони особливо важливі в ігрових задачах.

Знайдемо числові характеристики величини . Перевіримо спочатку виконання умови нормування. Розглянемо:

.

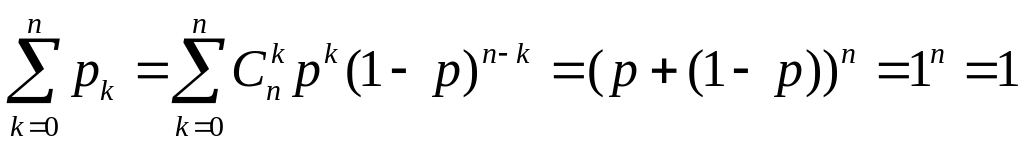Тут ми використали формулу бінома Ньютона:

(звідси й назва розподілу – біноміальний).

Знайдемо математичне сподівання величини . Тут можна використати два шляхи. Перший полягає у розгляді формального виразу для математичного сподівання величини :

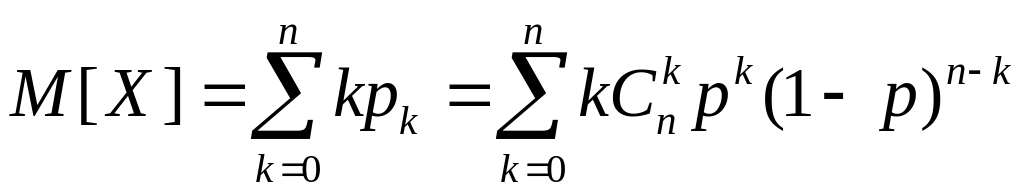та обчислення цієї суми. Але цей спосіб складний. Краще використати інший, який ґрунтується саме на тому, що величина – число появ події в випробуваннях.

Розглянемо випадкову величину , яку задано наступним законом розподілу:

	0	1

Тут . Така величина називається індикатором події . Вона дорівнює числу появ події в одному випробуванні, якщо . Знайдемо:

,

.

Повернемось до величини . Позначимо як – число появ події у -му випробуванні. Очевидно, що всі величини взаємно незалежні та мають один й той же закон розподілу, який збігається з законом розподілу величини . Тому , . Крім того, очевидно, що

.

Тому:

,

.

Приклад. Проводиться 10 кидань гральної кістки. Знайти математичне сподівання та дисперсію числа появ «шестірки».

Маємо: , ;

, .