2.8. Середньоквадратичне відхилення дискретної випадкової величини.
Використання дисперсії для врахування розсіяння значень випадкової величини навколо математичного сподівання має ту незручність, що змінює розмірність випадкової величини, адже визначається через її квадрат. Наприклад, якщо випадкова величина вимірюється в сантиметрах, то її дисперсія буде вимірюватись в квадратних сантиметрах. З метою уникнення такої незручності користуються іншою характеристикою розсіяння.
Означення.
Середньоквадратичним
відхиленням
випадкової величини
називається арифметичний квадратний
корінь з її дисперсії:
.
Приклад. Знайти середньоквадратичне відхилення ДВВ , яку задано законом розподілу:
|
4,3 |
5,1 |
10,6 |
|
0,2 |
0,3 |
0,5 |
Маємо:
;
;
;
.
Теорема. Середньоквадратичне відхилення суми скінченного числа взаємно незалежних випадкових величин дорівнює арифметичному квадратному кореню з суми квадратів середньоквадратичних відхилень цих величин:
.
Доведення.
Позначимо:
.
Тоді (див. п. 2.7, наслідок 1 з Властивості
4):
.
Звідси:
.
2.9. Числові характеристики середнього арифметичного однаково розподілених випадкових величин.
Нехай
– взаємно незалежні випадкові величини,
які мають один й той же розподіл, отже
однакові числові характеристики
(математичне сподівання та дисперсію):
.
Позначимо:
.
Тобто
величина
є середнє арифметичне випадкових величин
.
Нашою метою буде встановлення зв’язку
між числовими характеристиками величини
та числовими характеристиками величин
.
Почнемо з математичного сподівання. Розглянемо:
.
Математичне сподівання середнього арифметичного однаково розподілених взаємно незалежних випадкових величин дорівнює математичному сподіванню кожної з цих величин.
Розглянемо тепер дисперсію:
.
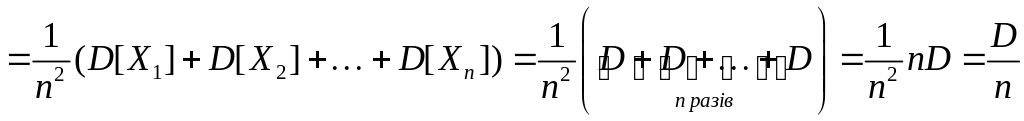Дисперсія середнього
арифметичного
однаково розподілених взаємно незалежних
випадкових величин в
разів менше дисперсії
кожної з цих величин.
Розглянемо середньоквадратичне відхилення:
.
Середньоквадратичне
відхилення середнього арифметичного
однаково розподілених взаємно незалежних
випадкових величин в
разів менше середньоквадратичного
відхилення
кожної з цих величин.
Об’єднуючи ці результати, можна зробити висновок, що середнє арифметичне досить великого числа однаково розподілених взаємно незалежних випадкових величин має значно менше розсіяння, ніж кожна з цих величин окремо. Цей результат має важливе прикладне значення. Нехай ми проводимо вимірювання деякої фізичної величини. Результат кожного вимірювання залежить від багатьох випадкових факторів, отже є величиною випадковою. Для знаходження значення шуканої фізичної величини,як правило, проводять не одне, а декілька вимірювань, а потім знаходять середнє арифметичне результатів всіх вимірювань. Чому так робиться? А ось як раз на підставі властивостей числових характеристик величини . Результати вимірювань, як випадкові величини, мають однаковий розподіл (якщо вимірювання проводяться одними й тими ж приладами, за однією і тою ж методикою), отже однакові числові характеристики. Вони взаємно незалежні (результат кожного вимірювання не залежить від інших вимірювань). Тоді середнє арифметичне результатів вимірювань матиме менше розсіяння, ніж кожне вимірювання окремо. Це означає, що середнє арифметичне має меншу похибку, отже дає більш точне наближення до шуканого результату, ніж результат одного окремого вимірювання. І це наближення буде тим точніше, чим більше вимірювань проведено.