2.41. Теорема Бернуллі.

Важливим наслідком теореми Чебишова є теорема Бернуллі, яка встановлює зв’язок між відносною частотою та ймовірністю події (див. п. 1.6). Цю теорему було доведено у 1713 році Я. Бернуллі (вона вперше й отримала назву закону великих чисел), а у 1846 році П. Л. Чебишов довів свою теорему, з якої теорема Бернуллі випливає як наслідок.

Теорема Бернуллі. Якщо у кожному з незалежних випробувань ймовірність появи події є сталою, то справджується гранична рівність:

, де – число появ події в випробуваннях.

Іншими словами, ймовірність того, що відхилення відносної частоти від ймовірності події за абсолютною величиною буде скільки завгодно малим, наближається до одиниці зі зростанням числа випробувань.

Доведення. Позначимо як – ДВВ, яка дорівнює числу появ події у 1-му випробуванні; як – ДВВ, яка дорівнює числу появ події у 2-му випробуванні; … ; як – числу появ події у -му випробуванні.

Закон розподілу кожної з величин має вигляд (див. п. 2.11):

	0	1

Тут . Перевіримо можливість застосування до величин теореми Чебишова. По-перше, треба, щоб ці величини були попарно незалежні. Це випливає з того, що незалежними є випробування. По-друге, треба, щоб вони мали скінченні математичні сподівання. Оскільки , то цю умову виконано. По-третє, треба, щоб вони мали рівномірно обмежені дисперсії. Розглянемо (див. п. 2.11):

.

Знайдемо найбільше значення функції на відрізку . Маємо: ; похідна перетворюється на нуль в точці ; . Отже , і таким чином дисперсії всіх величин не перевищують числа . Таким чином, третю умову також виконано, і ми можемо до величин застосувати теорему Чебишова.

Оскільки всі величини мають одне й те ж математичне сподівання , то наслідок з теореми Чебишова (див. п. 2.40) дає:

.

Покажемо, що . Дійсно, величина дорівнює числу появ події у -му випробуванні, отже сума дорівнює числу появ події у всіх випробуваннях, тобто саме . Отже

.

Враховуючи цю рівність, остаточно дістанемо:

, що й треба було довести.

Контрольні питання до розділу II.

1. Що таке випадкова величина? Які є види випадкових величин?

2. Що таке дискретна випадкова величина? Як вона задається?

3. Що таке математичне сподівання дискретної випадкової величини? Які його основні властивості та ймовірнісний зміст?

4. Що таке дисперсія дискретної випадкової величини? Які її основні властивості та ймовірнісний зміст?

5. Які особливості числових характеристик однаково розподілених взаємно незалежних випадкових величин?

6. Що таке початкові та центральні теоретичні моменти? Для чого вони використовуються?

7. Яка величина називається розподіленою за біноміальним розподілом? Чому дорівнюють математичне сподівання та дисперсія такої величини?

8. Яка величина називається розподіленою за законом Пуассона? Чому дорівнюють математичне сподівання та дисперсія такої величини?

9. Що таке неперервна випадкова величина? Що таке функція розподілу неперервної випадкової величини? Чи мають дискретні випадкові величини функцію розподілу?

10. Що таке щільність розподілу неперервної випадкової величини? У чому полягає її ймовірнісний зміст? Чи мають дискретні випадкові величини щільність розподілу?

11. Як визначаються математичне сподівання та дисперсія неперервної випадкової величини?

12. Яка величина називається розподіленою рівномірно на заданому відрізку? Чому дорівнюють математичне сподівання та дисперсія такої величини?

13. Яка величина називається розподіленою за показниковим законом? Чому дорівнюють математичне сподівання та дисперсія такої величини?

14. Яка величина називається розподіленою за нормальним законом? Чому дорівнюють математичне сподівання та дисперсія такої величини?

15. Як впливають параметри нормального розподілу на форму кривої Гауса?

16. У чому полягає правило «трьох сигм»?

17. Як оцінюються відхилення заданого розподілу від нормального?

18. У чому суть центральної граничної теореми Ляпунова?

19. Що таке двовимірні випадкові величини? Як задаються двовимірні дискретні випадкові величини?

20. Що таке функція розподілу двовимірної випадкової величини?

21. Що таке щільність розподілу двовимірної випадкової величини?

22. Які випадкові величини називаються незалежними?

23. Які характеристики системи двох випадкових величин характеризують тісноту зв’язку між ними?

24. Який зв’язок між корельованістю та залежністю випадкових величин?

25. У чому полягає суть закону великих чисел?

Вправи для самостійного розв’язування.

1. Серед 10 деталей 4 нестандартних. Навмання відбираються 3 деталі. Написати ряд розподілу випадкової величини – кількості нестандартних деталей серед 4-х відібраних.

2. На шляху руху автомобіля 6 світлофорів, кожен з яких дозволяє або забороняє рух автомобіля з ймовірністю 0,5. Скласти ряд розподілу і побудувати функцію розподілу кількості світлофорів, які автомобіль минув без зупинки. Чому дорівнює математичне сподівання та дисперсія цієї випадкової величини?

3. Знайти математичне сподівання дискретної випадкової величини – числа таких кидань п’яти гральних кісток, у кожному з яких на двох кістках з’явиться по одному очку, якщо загальне число кидань дорівнює 20.

4. Знайти закон розподілу дискретної випадкової величини , яка може приймати лише два значення: з ймовірністю 0,6 та ( ), якщо ; .

5. Знайти дисперсію дискретної випадкової величини – числа появ події в двох незалежних випробуваннях, якщо ймовірність появи події в кожному випробуванні однакова, і відомо, що .

6. Проводяться незалежні випробування з однаковою ймовірністю появи події в кожному випробуванні. Знайти ймовірність появи події , якщо дисперсія числа появ події в трьох незалежних випробуваннях дорівнює 0,63.

7. Задано функцію розподілу неперервної випадкової величини :

Знайти параметри і , а також ймовірність того, що внаслідок випробування величина прийме значення з проміжку .

8. Для величини з попередньої задачі знайти щільність розподілу. Побудувати графіки функції та щільності розподілу.

9. Задано щільність розподілу неперервної випадкової величини :

Знайти параметр і функцію розподілу величини . Побудувати графіки функції та щільності розподілу.

10. Задано щільність розподілу випадкової величини :

Знайти

1) параметр ;

2) функцію розподілу і побудувати графіки функції та щільності;

3) ймовірність того, що внаслідок випробування величина прийме значення з інтервалу ;

4) математичне сподівання, дисперсію та середньоквадратичне відхилення величини .

11. Задано щільність розподілу випадкової величини :

.

Знайти коефіцієнт , математичне сподівання та дисперсію величини .

12. Задано щільність розподілу випадкової величини :

.

Знайти

1) коефіцієнт ;

2) функцію розподілу величини ;

3) ймовірність того, що в двох незалежних випробуваннях величина прийме значення, менші за 1.

13. Вимірювальний прилад має систематичну похибку 5 м та середньоквадратичну похибку 75 м. Знайти ймовірність того, що похибка вимірювання не перевищить за абсолютною величиною 5 м, якщо вважати, що вона розподілена за нормальним законом.

14. Випадкова величина має нормальний розподіл, причому , . Що більше: або ?

15. Зважують деяку речовину без систематичних (тобто одного знаку) похибок. Випадкові похибки підпорядковані нормальному закону з середньоквадратичним відхиленням г. Знайти ймовірність того, що зважування буде виконано з похибкою, яка за абсолютною величиною на перевищує 10 г.

16. Випадкова величина розподілена нормально з параметром . Ймовірність потрапляння величини в інтервал (10, 20) дорівнює 0,3. Чому дорівнює ймовірність потрапляння величини в інтервал (0, 10)?

17. Задано закон розподілу двовимірної випадкової величини:

4	3	10	12
5	0,17 0,10	0,13 0,30	0,25 0,05

Знайти закони розподілу величин та .

18. Задано функцію розподілу двовимірної випадкової величини:

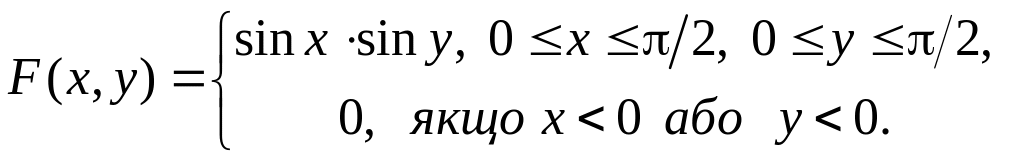
Знайти ймовірність потрапляння випадкової точки в прямокутник, обмежений прямими , , , .

19. Щільність розподілу двовимірної випадкової величини дорівнює в крузі . Зовні цього круга . Знайти:

1) параметр ;

2) ймовірність потрапляння випадкової точки в круг радіусу з центром у початку координат.

20. Двовимірну випадкову величину задано щільністю розподілу:

Знайти:

1) параметр ;

2) щільності розподілів складових та .

21. Користуючись нерівністю Чебишова, оцінити ймовірність того, що будь яка випадкова величина відхилиться від свого математичного сподівання менш, ніж на три середньоквадратичних відхилення цієї величини.

22. Дискретну випадкову величину задано законом розподілу:

	0,3	0,6
	0,2	0,8

Користуючись нерівністю Чебишова, оцінити ймовірність того, що .

23. Прилад складається з 10 незалежно працюючих елементів. Для кожного елемента ймовірність його відмови за час дорівнює 0,05. Користуючись нерівністю Чебишова, оцінити ймовірність того, що абсолютна величина різниці між числом елементів, що відмовили, і середнім числом (математичним сподіванням) відмов за час буде менша ніж 2.

24. Дано послідовність незалежних випадкових величин . Випадкова величина має закон розподілу:

		0

Чи можна застосувати до цієї послідовності теорему Чебишова?

25. Дано послідовність незалежних випадкових величин . Випадкова величина має закон розподілу:

Чи можна застосувати до цієї послідовності теорему Чебишова?

1 Чебишов Пафнутій Львович (1821–1894) – видатний російський математик.

154