2.40. Теорема Чебишова (закон великих чисел).

Теорема Чебишова. Якщо – попарно незалежні випадкові величини, які мають скінченні математичні сподівання, причому дисперсії цих величин рівномірно обмежені, тобто : , то для будь якого числа виконано граничну рівність:

.

Тобто якщо розглядається достатньо велика кількість незалежних випадкових величин, що мають обмежені дисперсії, то практично достовірною можна вважати подію, яка полягає в тому, що відхилення середнього арифметичного випадкових величин від середнього арифметичного їх математичних сподівань буде за абсолютною величиною як завгодно малим.

Доведення. Розглянемо наступну випадкову величину:

, тобто середнє арифметичне величин . Знайдемо

.

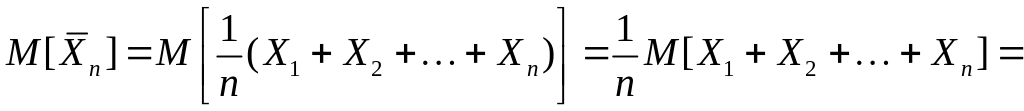
Використовуючи нерівність Чебишова, дістанемо:

.

Або:

.

За властивостями дисперсії можемо записати:

.

Оскільки , то:

.

Отже:

.

Переходячи в цій рівності до границі при , отримаємо:

.

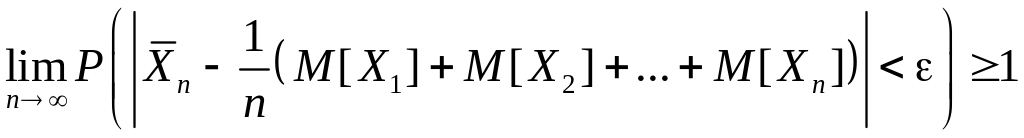Але, враховуючи те, що ймовірність події не може перевищувати одиниці, остаточно маємо:

.

Теорему доведено.

Наслідок. Якщо – попарно незалежні випадкові величини, що мають одне й те ж математичне сподівання , та якщо дисперсії цих величин рівномірно обмежені, то для будь якого числа справджується:

.

Доведення. Дійсно, якщо , то

, і, користуючись теоремою Чебишова, отримуємо потрібне.

Теорема Чебишова стверджує, що, хоча незалежні випадкові величини можуть приймати значення, які значно відрізняються від своїх математичних сподівань, середнє арифметичне досить великого числа випадкових величин з великою ймовірністю приймає значення, близькі до певного сталого числа. Таким чином це середнє з випадкового перетворюється фактично на закономірне.

Теорема Чебишова має велике значення для практики. Розглянемо такий приклад. Нехай ми проводимо вимірювання деякої фізичної величини. Як зазвичай одним вимірюванням не обмежуються, а проводять декілька вимірювань, і в якості шуканого значення приймають середнє арифметичне результатів вимірювань. За яких умов цей спосіб є виправданим? Відповідь на це питання дає теорема Чебишова (точніше, наслідок з неї). Дійсно, розглянемо результати всіх вимірювань як випадкові величини . До цих величин можна застосувати теорему Чебишова, якщо: 1) вони попарно незалежні; 2) мають одне й те ж математичне сподівання; 3) їх дисперсії рівномірно обмежені. Перша з цих умов виконуються, якщо результат кожного вимірювання не залежить від результатів інших вимірювань. Друга умова виконується, якщо вимірювання проведено без систематичних (одного знаку) похибок. У цьому випадку математичні сподівання всіх випадкових величин однакові і дорівнюють шуканому значенню . Третя умова виконується, якщо прилад, яким проводяться вимірювання, забезпечує певну їх точність.

Якщо всі ці умови виконано, можемо застосувати теорему Чебишова. Відповідно неї ймовірність нерівності

при достатньо великих стає як завгодно близькою до одиниці. Іншими словами, при достатньо великій кількості вимірювань майже достовірно, що середнє арифметичне їх результатів як завгодно мало відрізняється від шуканого значення величини, що вимірюється.

На теоремі Чебишова ґрунтується вибірковий метод у статистиці. Це питання розглядається у Розділі III.

Приклад. Послідовність незалежних випадкових величин задано законами їх розподілів:

		0

Чи можна застосувати до цієї послідовності теорему Чебишова?

Для того, щоб до послідовності величин можна було застосувати теорему Чебишова, достатньо, щоб ці величини були попарно незалежні, мали скінченні математичні сподівання та рівномірно обмежені дисперсії.

Оскільки дані величини незалежні, то вони й попарно незалежні, тобто першу умову теореми Чебишова виконано. Розглянемо математичні сподівання:

.

Таким чином, другу умову також виконано. Знайдемо дисперсії:

.

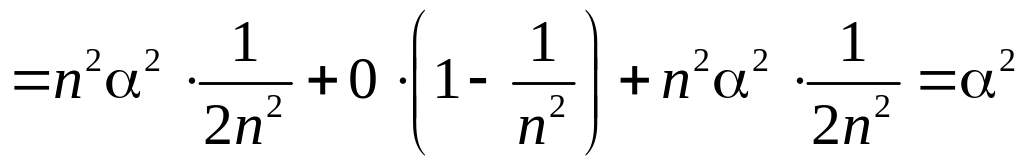Таким чином, всі дисперсії рівномірно обмежені числом , і третю умову також виконано.

Отже до даної послідовності можна застосувати теорему Чебишова.