2.37. Корельованість та залежність випадкових величин.

Означення. Дві випадкові величини та називаються корельованими, якщо їх кореляційний момент відмінний від нуля (це еквівалентно тому, що коефіцієнт кореляції відмінний від нуля). Відповідно, величини та називаються некорельованими, якщо їх кореляційний момент дорівнює нулю.

Дві корельовано величини також є й залежними. Дійсно, якби вони були незалежні, то їх кореляційний момент дорівнював би нулю (див. п. 2.36), а це суперечить тому, що величини корельовано.

Чи можна стверджувати обернене, тобто що з залежності величин випливає їх корельованість? З’ясовується, що не завжди. Кореляційний момент залежних величин може бути відмінним від нуля, але може й дорівнювати нулю.

Приклад. Нехай двовимірну випадкову величину задано щільністю розподілу (див. п. 2.34):

Доведемо, що величини та залежні. В п. 2.34 було обчислено щільності розподілу компонент та :

Оскільки , то величини та залежні (див. п. 2.35). Знайдемо кореляційний момент цих величин за формулою:

.

Внаслідок парності функцій , , отже симетрії їх графіків відносно вертикалі для функції і вертикалі для функції , можемо зробити висновок, що , отже:

.

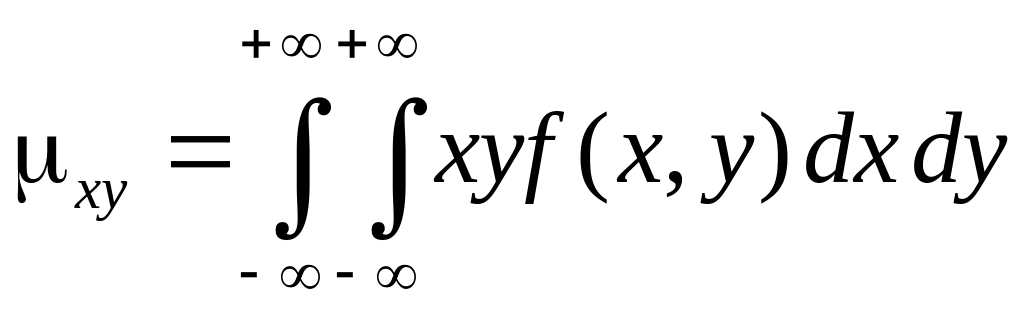Оскільки відмінна від нуля тільки всередині еліпсу , то

.

Інтеграл

дорівнює нулю, як інтеграл у симетричних межах від непарної функції, отже , тобто величини та некорельовані.

Таким чином, з корельованості двох випадкових величин випливає їх залежність, але з залежності не випливає корельованість. Навпаки, з незалежності двох випадкових величин випливає їх некорельованість, але з некорельованості не випливає незалежність.

2.38. Двовимірний закон нормального розподілу.

Означення. Двовимірним нормальним законом розподілу називається закон розподілу двовимірної величини , якщо щільність розподілу має вигляд:

. (*)

Поверхню в тривимірному просторі, що є «графіком» функції , наведено на рис. 39.

З формули (*) видно, що двовимірний нормальний закон розподілу характеризується п’ятьма параметрами: . Можна довести, що ці параметри мають наступний ймовірнісний зміст: – математичні сподівання відповідно компонент та ; – їх середньоквадратичні відхилення; – коефіцієнт кореляції.

Теорема. Якщо компоненти та двовимірної нормально розподіленої випадкової величини некорельовані, то та є незалежними.

Доведення. Оскільки та некорельовані, то . Тоді щільність розподілу набуває вигляду:

.

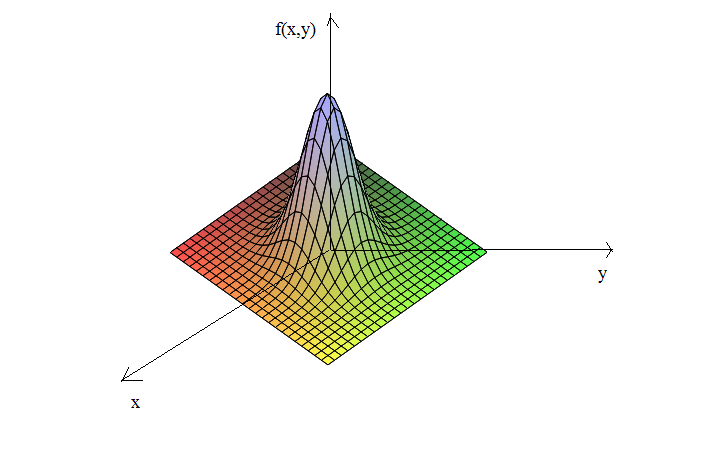
Рис. 39.

Таким чином щільність сумісного розподілу системи дорівнює добутку щільностей розподілів величин та , а це означає, що величини та незалежні.

Наслідок. Для того, щоб компоненти та двовимірної нормально розподіленої випадкової величини були некорельовані, необхідно і достатньо, щоб величини та були незалежні.