2.35. Залежні та незалежні випадкові величини.

Ми вже знаємо (див. п. 2.5), що дві випадкові величини і називаються незалежними, якщо закон розподілу однієї з них не залежить від того, які можливі значення прийняла інша величина. Знайдемо необхідні та достатні умови незалежності випадкових величин.

Теорема. Для того, щоб випадкові величини і були незалежними, необхідно і достатньо, щоб функція розподілу системи дорівнювала добутку функцій розподілу складових:

.

Доведення. Необхідність. Нехай і незалежні. Тоді події та також незалежні, отже

, або

, і таким чином необхідність доведено.

Достатність. Нехай . Звідси

.

Тобто ймовірність сумісної появи подій та дорівнює добутку ймовірностей цих подій. Це означає, що ці події незалежні, отже незалежні величини і .

Наслідок. Для того, щоб неперервні випадкові величини і були незалежними, необхідно і достатньо, щоб щільність розподілу системи дорівнювала добутку щільностей розподілів складових:

.

Доведення. Необхідність. Нехай і – незалежні неперервні випадкові величини. Тоді на підставі попередньої теореми:

.

Диференцюючи цю рівність спочатку за , а потім за , дістанемо:

.

Або:

, і необхідність доведено.

Достатність. Нехай

.

Інтегруючи цю рівність за і за , дістанемо:

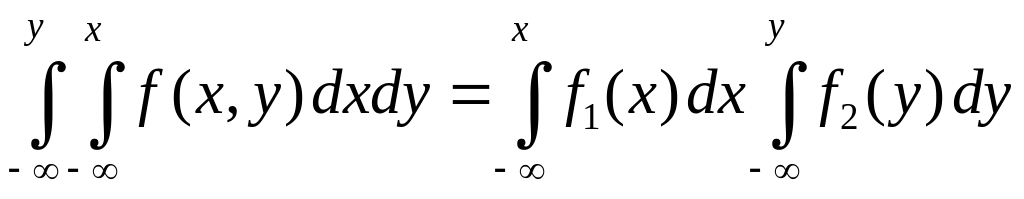, або

.

Звідси на підставі попередньої теореми випливає, що величини та незалежні.

2.36. Числові характеристики системи двох випадкових величин.

Для опису системи двох випадкових величин використовують також інтегральні її характеристики. До них відносяться математичні сподівання та дисперсії компонент, а також інші характеристики – кореляційний момент і коефіцієнт кореляції.

Означення. Кореляційним моментом системи двох випадкових величин називається математичне сподівання добутку відхилень цих величин від своїх математичних сподівань:

.

Зокрема, якщо величини є дискретними, то

.

А якщо величини є неперервними, то

.

Кореляційний момент характеризує зв’язок між величинами та .

Зауваження. Кореляційний момент може бути записано у вигляді:

.

Дійсно:

.

Теорема. Кореляційний момент двох незалежних випадкових величин та дорівнює нулю.

Доведення. Оскільки та незалежні, то

.

А тоді

.

Кореляційний момент має розмірність, що дорівнює добутку розмірностей величин та . Отже величина кореляційного моменту залежить від одиниць виміру випадкових величин. За цією причиною для одних й тих ж випадкових величин величина кореляційного моменту може мати різні значення в залежності від того, в яких одиницях вимірено величини та . Така особливість кореляційного моменту створює незручності при користуванні ним, отже є його недоліком. Для подолання цього недоліку вводиться інша числова характеристика – коефіцієнт кореляції.

Означення. Коефіцієнтом кореляції випадкових величин та називається відношення кореляційного моменту цих величин до добутку їх середньоквадратичних відхилень:

.

Розмірність дорівнює добутку розмірностей величин та , має розмірність величини , а має розмірність величини . Отже – безрозмірна величина.

Якщо та незалежні, то , оскільки .

Теорема. Абсолютна величина кореляційного моменту двох випадкових величин та не перевищує добутку їх середньоквадратичних відхилень:

. (*)

Доведення. Введемо до розгляду випадкову величину і знайдемо її дисперсію:

.

Оскільки будь яка дисперсія невід’ємна, то

, звідки

.

Вводячи випадкову величину , аналогічно знайдемо:

.

Таким чином задовольняє подвійну нерівність:

, яка еквівалентна нерівності:

, що й треба було довести.

Наслідок. Абсолютна величина коефіцієнту кореляції не перевищує одиниці:

.

Для доведення достатньо поділити обидві частини нерівності (*) на .

Як і кореляційний момент, коефіцієнт кореляції випадкових величин та характеризує зв’язок між цими величинами. Чим модуль коефіцієнта кореляції ближче до одиниці, тим цей зв’язок більш суттєвий.

Приклад. Щільність розподілу двовимірної випадкової величини задано формулою:

де

.

Знайти , , .

Щільності компонент знаходимо за формулами:

.

В даному випадку маємо:

, , тобто

Аналогічно:

Знайдемо математичні сподівання компонент:

.

Аналогічно:

.

Знайдемо дисперсії:

.

Отже:

.

Аналогічно:

.

Знайдемо кореляційний момент:

.

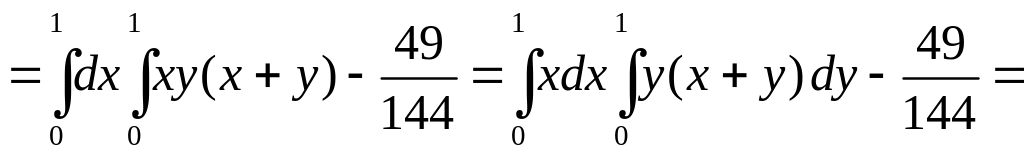
Тепер знайдемо коефіцієнт кореляції:

.