2.33. Функція розподілу двовимірної випадкової величини.

Розглянемо двовимірну випадкову величину . Нехай – пара дійсних чисел.

Означення. Функцією розподілу двовимірної випадкової величини називається функція , яка дорівнює ймовірності добутку подій та :

.

З геометричної точки зору є ймовірність того, що випадкова точка потрапить у нескінченний прямокутник з вершиною у точці та розміщений нижче та лівіше цієї вершини (прямі ліній, що утворюють верхню та праву межу цього прямокутника, до нього не включаються) (рис. 38).

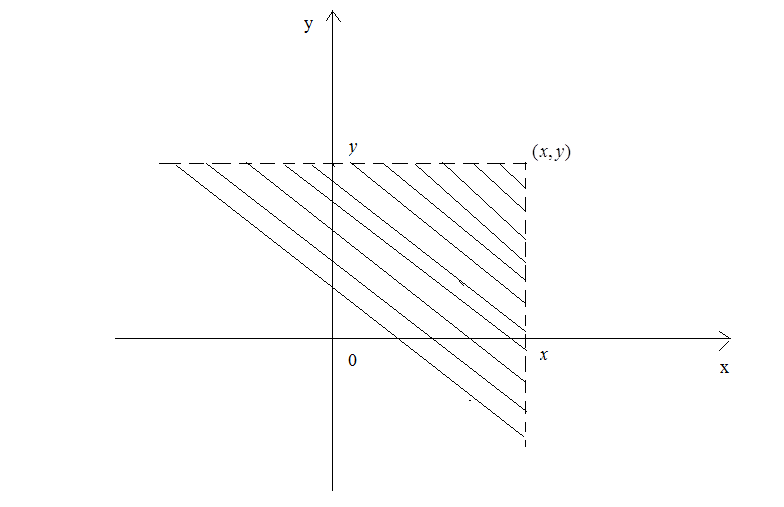
Рис. 38.

Приклад. Знайти , якщо

.

Маємо:

.

З’ясуємо властивості функції розподілу двовимірної випадкової величини. Вони певною мірою аналогічні властивостям функції розподілу одновимірної випадкової величини.

Властивість 1. Всі значення функції розподілу задовольняють нерівність:

.

Доведення випливає з того, що функція розподілу за означенням є ймовірність, а будь яка ймовірність є число з відрізку .

Властивість 2. Функція неспадна за кожним аргументом, тобто

, якщо ;

, якщо .

Доведення. Доведемо, що функція неспадна за аргументом . Розглянемо подію:

.

За теоремою про ймовірність суми несумісних подій:

, оскільки . Таким чином:

, що й треба було довести.

Аналогічно доводиться, що функція неспадна також за аргументом .

Властивість 3. Справедливі граничні співвідношення:

1) ; 2) ; 3) ; 4) .

Доведення. 1) є ймовірність події , але така подія неможлива, оскільки неможлива подія , отже ймовірність цієї події дорівнює нулю.

2) , оскільки подія неможлива.

3) , оскільки подія неможлива.

4) , оскільки події , достовірні.

Властивість 4. При функція розподілу двовимірної випадкової величини перетворюється на функцію розподілу складової :

.

При функція розподілу двовимірної випадкової величини перетворюється на функцію розподілу складової :

.

Доведення. Розглянемо:

;

.

2.34. Щільність розподілу неперервної двовимірної випадкової величини.

Означення. Щільністю розподілу неперервної двовимірної випадкової величини називається невід’ємна функція:

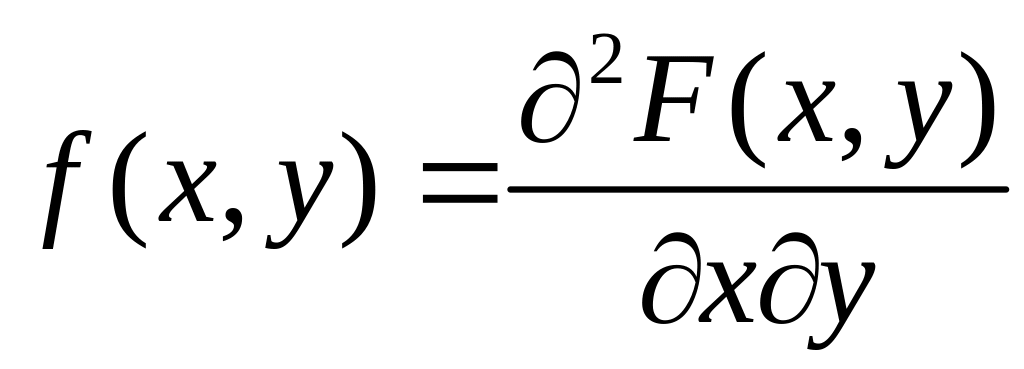, де – функція розподілу величини .

Приклад. Функцію розподілу двовимірної випадкової величини задано формулою:

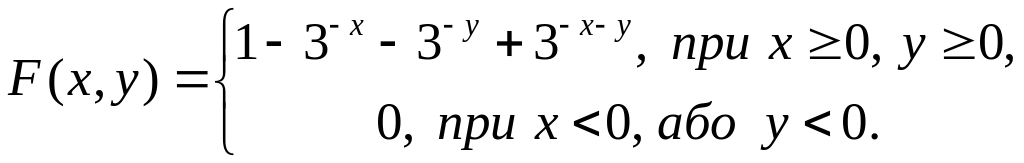
Знайти щільність даного розподілу.

Знайдемо частинні похідні від . При маємо:

, .

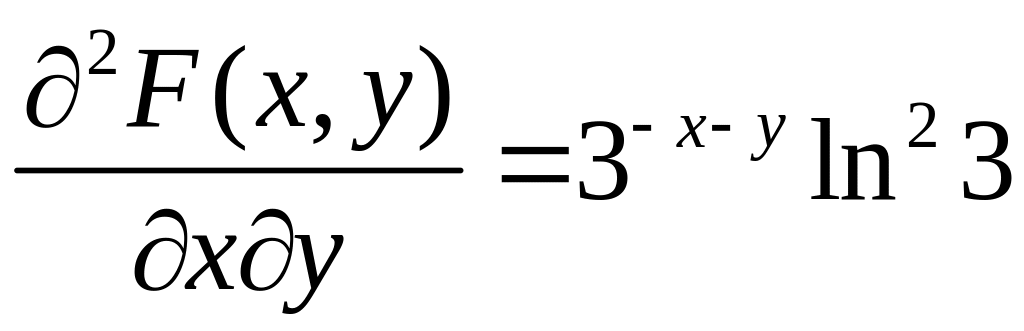Таким чином:

Знаючи щільність розподілу, можна знайти функцію розподілу за формулою:

.

Приклад. Нехай щільність розподілу задано формулою:

.

Знайти функцію розподілу:

Маємо:

.

Нехай задано довільну область на площині . Тоді ймовірність потрапляння випадкової точки в область визначається формулою:

.

Звідси, зокрема, буде випливати умова нормування для щільності розподілу:

.

Зокрема, якщо відмінна від нуля лише в деякій області , то

.

Приклад. Щільність розподілу двовимірної випадкової величини задається так: в крузі . А зовні цього круга . Знайти сталу та ймовірність потрапляння випадкової точки в круг .

Скористаємось умовою нормування. Маємо:

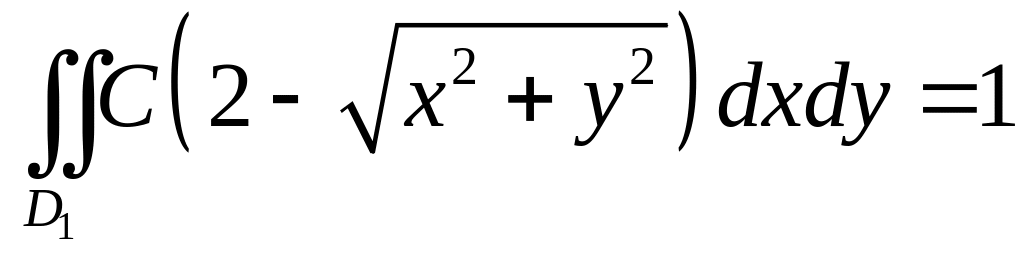, де

.

Або

.

Обчислимо інтеграл:

.

Перейдемо у цьому інтегралі до полярних координат:

.

Дістанемо:

.

Звідси:

.

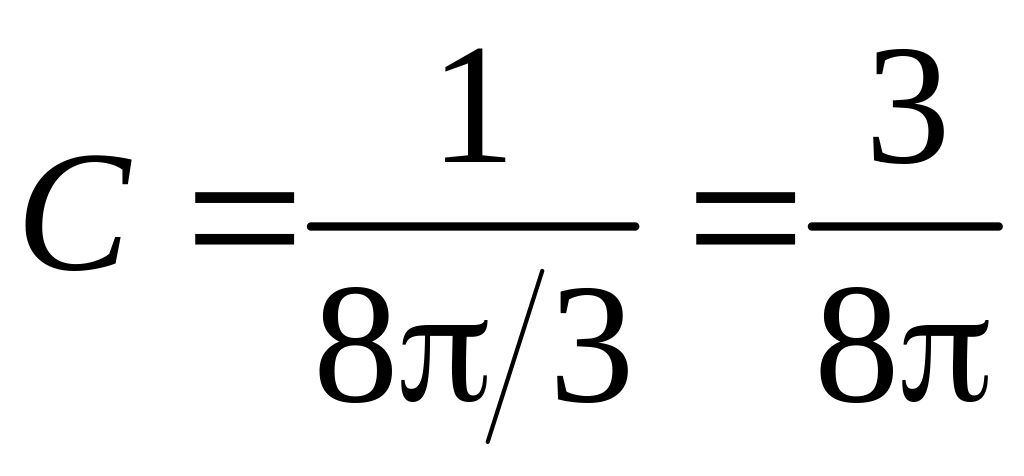Таким чином:

в крузі . Знайдемо тепер ймовірність потрапляння точки в круг :

=

.

Якщо відомо щільність сумісного розподілу системи , то можна знайти щільності розподілу компонент та . Нехай – функція розподілу компоненти . Тоді щільність розподілу компоненти дорівнює:

.

З огляду на співвідношення

, знайдемо:

.

Звідси:

, або

.

Аналогічно:

.

Приклад. Двовимірну випадкову величину задано щільністю розподілу:

Знайти щільності розподілу складових і .

Знайдемо:

.

Отже

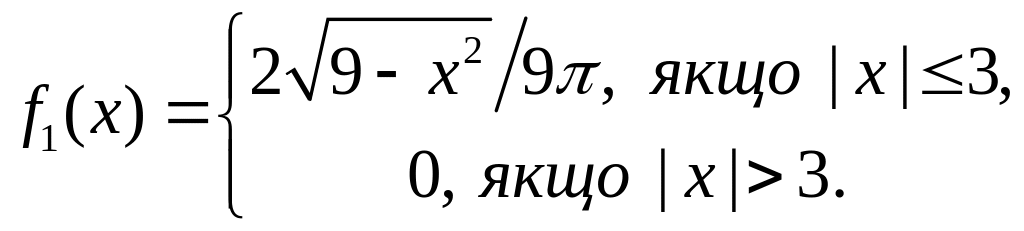
Аналогічно