2.31. Деякі інші важливі розподіли.

Розглянемо деякі інші розподіли, які зустрічаються в прикладних задачах.

1. Розподіл Лапласа

Цей розподіл визначається щільністю:

, , де – параметри розподілу. Графік наведено на рис. 32.

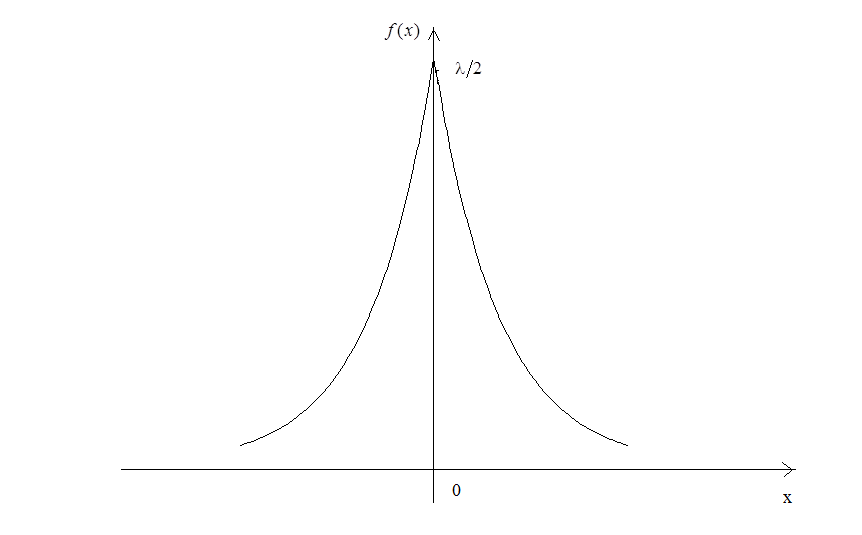
Рис. 32.

Розподілу Лапласа підпорядковуються, наприклад, похибки в моделях регресії.

Числові характеристики розподілу Лапласа:

, , .

2. Логнормальний розподіл.

Випадкова величина називається логарифмічно нормальною, якщо розподілено за нормальним законом. Логнормальний розподіл використовується, наприклад, при моделюванні таких змінних, як прибуток, допустиме відхилення від стандарту відсотків шкідливих речовин у харчових продуктах тощо. Щільність розподілу має вигляд:

, , – параметри. Графік наведено на рис. 33.

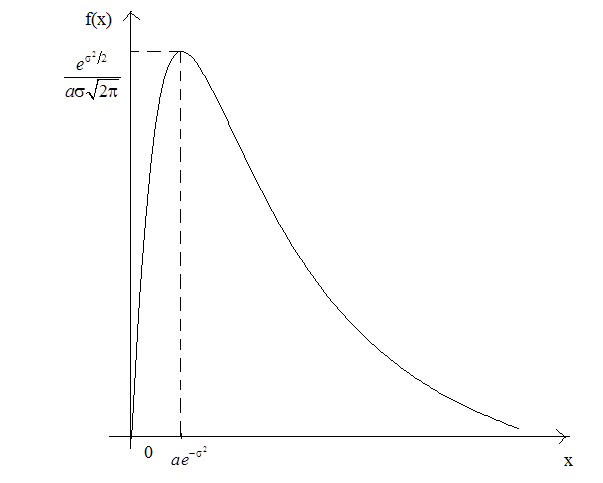
Рис. 33.

Числові характеристики цього розподілу наступні:

, , .

3. Розподіл арксинусу.

Випадкова величина називається розподіленою за законом арксинусу, якщо її щільність розподілу має вигляд:

Графік щільності наведено на рис.34.

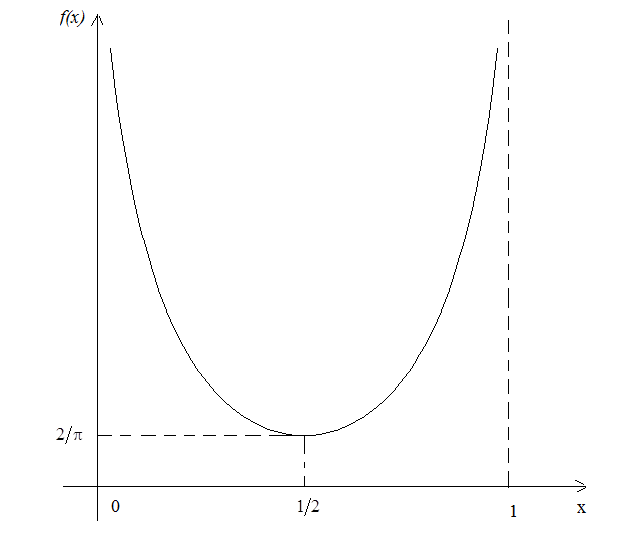
Рис. 34.

Знайдемо функцію розподілу.

а) : .

б) :

.

в) : .

Отже

Графік функції наведено на рис. 35.

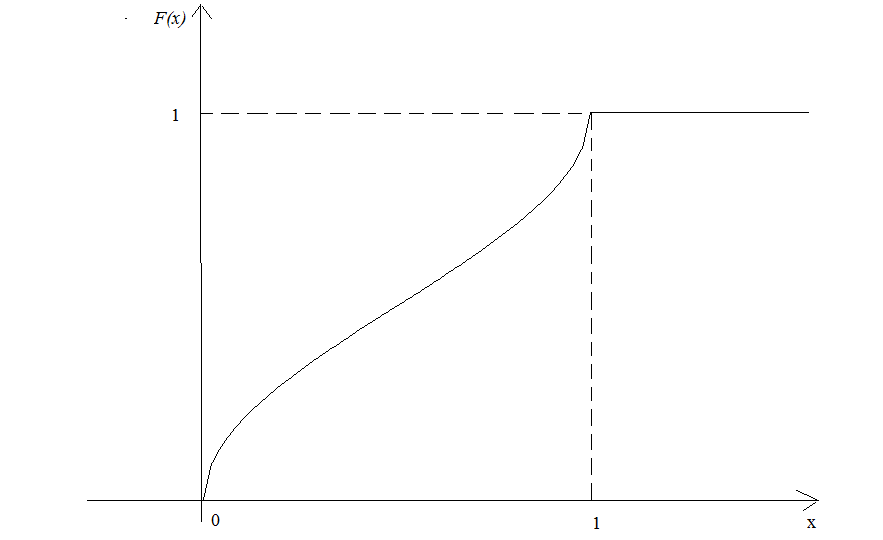
Рис. 35.

Числові характеристики розподілу арксинусу:

, , .

4. Розподіл Коші.

Випадкова величина називається розподіленою за законом Коші, якщо щільність розподілу має вигляд:

, .

Графік щільності наведено на рис. 36.

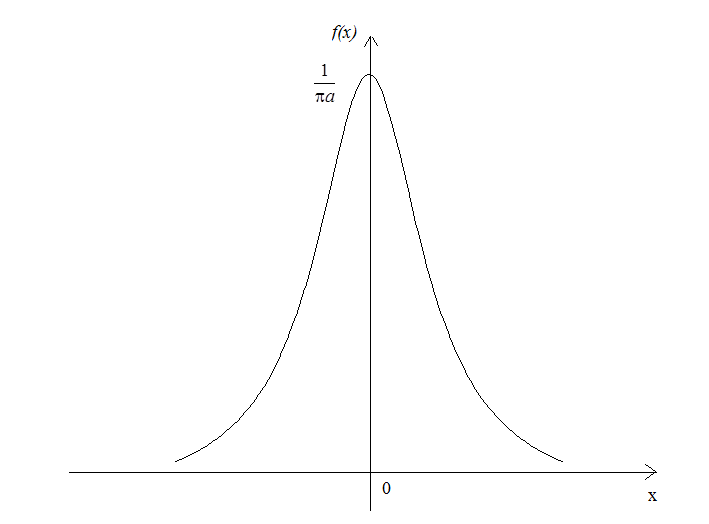
Рис. 36.

Функція розподілу Коші така:

, .

Графік наведено на рис. 37.

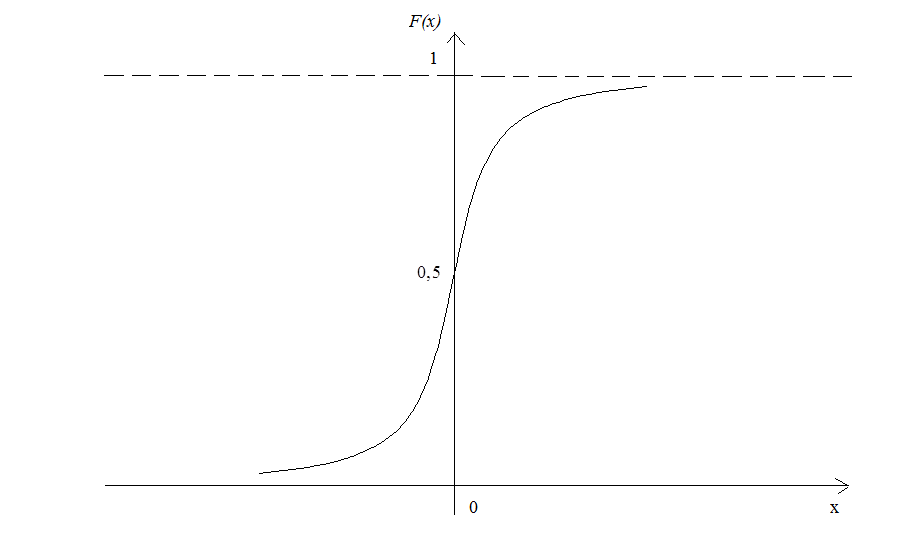
Рис. 37.

А ось математичного сподівання та дисперсії розподілу Коші не існує внаслідок того, що інтеграли

,

розбіжні.

2.32. Двовимірні випадкові величини. Закон розподілу дискретної двовимірної випадкової величини.

У попередніх параграфах ми розглядали випадкові величини, можливі значення яких визначалися одним числом. Такі величини називаються одновимірними. Разом з цим зустрічаються випадкові величини, можливі значення яких визначаються декількома числами. Наприклад, з набору кісток доміно навмання вибирається одна кістка. На кожній кістці є два числа, наприклад, 2:5, або 6:0, або 3:3. Ці числа у сукупності можна розглядати як випадкову величину, можливі значення якої виражаються двома числами. Або нехай на координатну площину випадковим чином потрапляє точка. Положення цієї точки визначається двома незалежними числами – координатами цієї точки. Ці координати у сукупності також є випадковою величиною, можливі значення якої виражаються двома числами. Є й величини, можливі значення яких виражаються трьома, декількома числами. Такі величини називаються багатовимірними. Зокрема, двовимірними, тривимірними, тощо.

Будемо розглядати двовимірні випадкові величини. Позначатимемо такі величини як . Кожну з величин та називають складовою (або компонентою). Обидві величини та , що розглядаються одночасно, утворюють систему двох випадкових величин. Її також можна інтерпретувати як вектор на площині з компонентами та . Тому також використовується термін випадковий вектор .

Якщо величини та дискретні, то двовимірна випадкова величина також називається дискретною.

Означення. Законом розподілу дискретної двовимірної випадкової величини називається таблиця, яка містить перелік всіх можливих значень цієї величини, а також ймовірності цих значень.

Тобто: .

Події утворюють повну групу. Тому

(умова нормування).

Знаючи закон розподілу двовимірної дискретної випадкової величини, можна знайти закони розподілу кожної з компонент. Дійсно, події, наприклад, , , …, несумісні, тому ймовірність за теоремою про ймовірність суми подій така:

.

Таким чином дорівнює сумі ймовірностей, що містяться у першому стовпці таблиці розподілу. Відповідно дорівнює сумі ймовірностей, що містяться у -му стовпці таблиці. Аналогічно дорівнює сумі ймовірностей, що містяться у -му рядку таблиці.

Приклад. Задано закон розподілу двовимірної випадкової величини:

	26	30	41	50
2,3	0,05	0,12	0,08	0,04
2,7	0,09	0,30	0,11	0,21

Знайти закони розподілу компонент та .

Маємо:

;

;

;

;

;

.

Отже

	26	30	41	50
	0,14	0,42	0,19	0,25

	2,3	2,7
	0,29	0,71