
- •Розділ II. Випадкові величини.
- •2.1. Випадкові величини, їх види.
- •2.2. Дискретні випадкові величини. Закон розподілу.
- •2.3. Задачі на побудову закону розподілу дискретної випадкової величини.
- •2.4. Математичне сподівання дискретної випадкової величини.
- •2.5. Основні властивості математичного сподівання.
- •2.6. Ймовірнісний зміст математичного сподівання.
- •2.7. Дисперсія дискретної випадкової величини.
- •2.8. Середньоквадратичне відхилення дискретної випадкової величини.
- •2.9. Числові характеристики середнього арифметичного однаково розподілених випадкових величин.
- •2.10. Початкові та центральні теоретичні моменти.
- •2.11 Біноміальний розподіл.
- •2.12. Розподіл Пуассона.
- •2.13. Геометричний розподіл.
- •2.14. Неперервні випадкові величини. Функція розподілу.
- •2.15. Властивості функції розподілу.
- •2.16. Функція розподілу дискретної випадкової величини.
- •2.17. Щільність розподілу неперервної випадкової величини.
- •2.18. Властивості щільності розподілу.
- •2.19. Ймовірнісний зміст щільності розподілу.
- •2.20. Числові характеристики неперервних випадкових величин.
- •2.21. Рівномірний розподіл.
- •2.22. Показниковий розподіл.
- •2.23. Показниковий закон надійності.
- •2.24. Нормальний розподіл.
- •2.25. Нормальна крива та вплив параметрів нормального розподілу на її форму.
- •2.26. Ймовірність потрапляння нормальної випадкової величини в заданий інтервал.
- •2.27. Ймовірність заданого відхилення. Правило «трьох сигм».
- •2.28. Задачі на нормальний розподіл.
- •2.29. Відхилення заданого розподілу від нормального. Асиметрія та ексцес.
- •2.30. Поняття про центральну граничну теорему. Значення нормально розподілених випадкових величин.
- •2.31. Деякі інші важливі розподіли.
- •2.32. Двовимірні випадкові величини. Закон розподілу дискретної двовимірної випадкової величини.
- •2.33. Функція розподілу двовимірної випадкової величини.
- •2.34. Щільність розподілу неперервної двовимірної випадкової величини.
- •2.35. Залежні та незалежні випадкові величини.
- •2.36. Числові характеристики системи двох випадкових величин.
- •2.37. Корельованість та залежність випадкових величин.
- •2.38. Двовимірний закон нормального розподілу.
- •2.39. Нерівність Чебишова.
- •2.40. Теорема Чебишова (закон великих чисел).
- •2.41. Теорема Бернуллі.
2.29. Відхилення заданого розподілу від нормального. Асиметрія та ексцес.
Випадкові величини, які реально зустрічаються на практиці, хоча можуть бути близькими до нормальних, але їх розподіл, взагалі кажучи, не збігається точно з нормальним, а дещо від нього відрізняється. І тому виникає необхідність ці відмінності оцінювати. З цією метою вводяться такі характеристики, як асиметрія та ексцес. Можна довести, що для нормального розподілу ці характеристики дорівнюють нулю. Тому якщо для реального розподілу вони є невеликими, то можна припустити, що даний розподіл близький до нормального.
Означення. Асиметрією даного розподілу називається відношення центрального моменту 3-го порядку даного розподілу до куба його середньоквадратичного відхилення:
![]() .
.
Для
нормального розподілу (і взагалі для
будь якого симетричного розподілу,
зокрема, рівномірного)
![]() .
Якщо
.
Якщо
![]() ,
то графік даного розподілу вже не є
симетричним відносно прямої
,
то графік даного розподілу вже не є
симетричним відносно прямої
![]() .
У випадку
.
У випадку
![]() частина графіка щільності, що розташована
справа від прямої
,
є більш пологою, а частина, що розташована
зліва, більш крутою (рис. 29).
частина графіка щільності, що розташована
справа від прямої
,
є більш пологою, а частина, що розташована
зліва, більш крутою (рис. 29).

Рис. 29.
У
випадку
![]() ситуація протилежна: ліва частина
графіка більш полога, а права – більш
крута (рис. 30).
ситуація протилежна: ліва частина
графіка більш полога, а права – більш
крута (рис. 30).
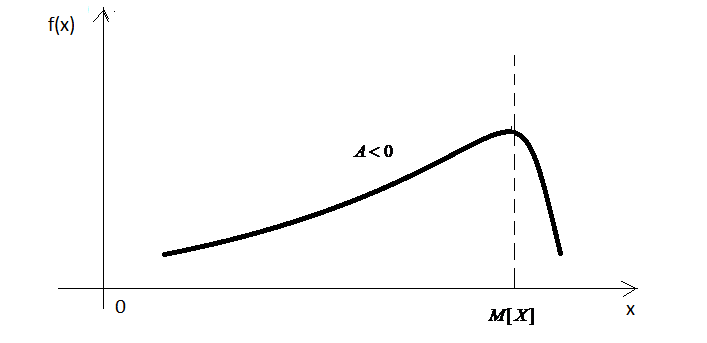 Рис.
30.
Рис.
30.
Для оцінки «крутизни» графіка, тобто більшого чи меншого його підйому в околі математичного сподівання порівняно з нормальним розподілом, використовують таку характеристику, як ексцес.
Означення. Ексцесом даного розподілу називається характеристика, що визначається рівністю:
![]() .
.
Знову
ж таки, для нормального розподілу
![]() .
Тому, якщо
.
Тому, якщо
![]() ,
то даний розподіл відрізняється від
нормального, але якщо
,
то даний розподіл відрізняється від
нормального, але якщо
![]() ,
то можна вважати, що розподіл близький
до нормального.
,
то можна вважати, що розподіл близький
до нормального.
При
![]() крива даного розподілу має більш високу
і гостру верхівку, крива більш крута
порівняно з нормальною. При
крива даного розподілу має більш високу
і гостру верхівку, крива більш крута
порівняно з нормальною. При
![]() крива розподілу має більш низьку і
пологу верхівку порівняно з нормальною
(рис. 31).
крива розподілу має більш низьку і
пологу верхівку порівняно з нормальною
(рис. 31).
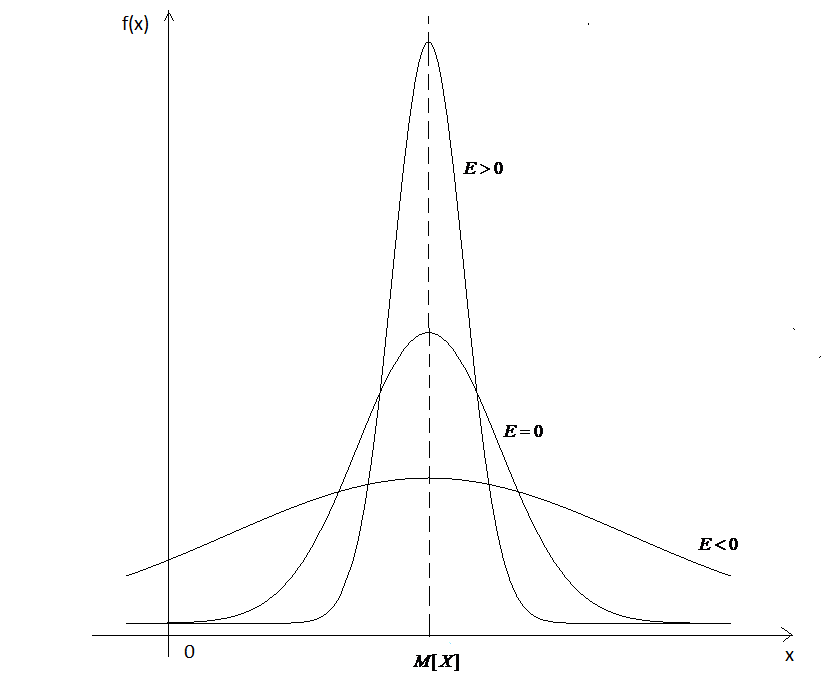
Рис. 31.
2.30. Поняття про центральну граничну теорему. Значення нормально розподілених випадкових величин.
Нормально розподілені випадкові величини відіграють дуже помітну роль в різноманітних процесах. Нормальному закону підпорядковуються, наприклад, похибки вимірювань, оцінки потужності геологічних порід, вміст хімічних елементів у породах. Пояснюється це наступним фактом: якщо ми маємо суму дуже великого числа взаємно незалежних випадкових величин, вплив кожної з яких на всю суму зовсім незначний, то вся сума має розподіл, близький до нормального. Цей факт доведено строго математично і має назву центральної граничної теореми О. М. Ляпунова.
Нехай
![]() – послідовність взаємно незалежних
випадкових величин, кожна з яких має
скінченні математичне сподівання та
дисперсію:
– послідовність взаємно незалежних
випадкових величин, кожна з яких має
скінченні математичне сподівання та
дисперсію:
![]() ,
,
![]() .
.
Позначимо:
 ,
,
 ,
,
 .
.
Очевидно тоді, що
![]() ,
,
![]() ,
,
![]() .
.
Випадкова величина
 тоді
є нормованою. Позначимо її функцію
розподілу як
тоді
є нормованою. Позначимо її функцію
розподілу як
![]() :
:
 .
.
Кажуть, що до послідовності можна застосувати центральну граничну теорему, якщо для будь якого виконано:
 .
.
Тобто
функція розподілу нормованої величини
![]() при
при
![]() прямує до функції розподілу нормальної
нормованої величини. Зокрема, якщо всі
випадкові величини
однаково розподілені, то до цієї
послідовності можна застосувати
центральну граничну теорему, якщо
дисперсії всіх величин
прямує до функції розподілу нормальної
нормованої величини. Зокрема, якщо всі
випадкові величини
однаково розподілені, то до цієї
послідовності можна застосувати
центральну граничну теорему, якщо
дисперсії всіх величин
![]() скінченні та відмінні від нуля. О. М.
Ляпунов довів, що якщо відношення
скінченні та відмінні від нуля. О. М.
Ляпунов довів, що якщо відношення
 ,
де
,
де
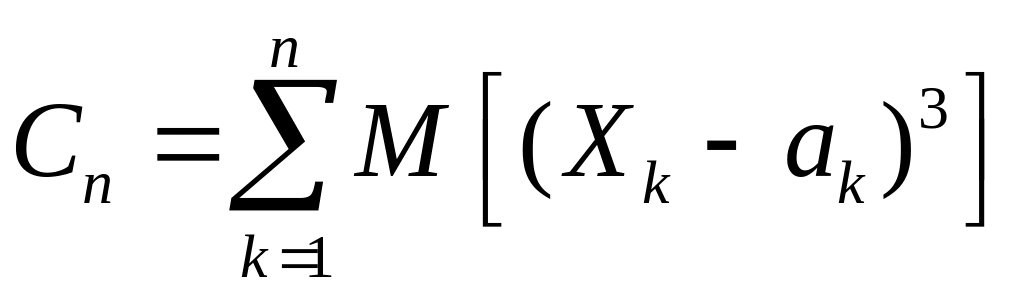 ,
прямує до нуля, то до
послідовності
можна застосувати центральну граничну
теорему.
,
прямує до нуля, то до
послідовності
можна застосувати центральну граничну
теорему.
