2.24. Нормальний розподіл.

В практичних задачах досить часто доводиться мати справу з випадковими величинами, які мають тенденцію групування навколо деякого середнього значення. Наприклад, якщо замірювати зріст студентів курсу, можна помітити, що більшість буде мати зріст, близький до середнього. Хоча, напевно, будуть студенти, що мають зріст помітно більше середнього, чи помітно менший, але таких студентів буде порівняно небагато. Такі випадкові величини називаються нормальними.

Означення. НВВ називається розподіленою за нормальним законом з параметрами і , якщо щільність її розподілу має вигляд:

.

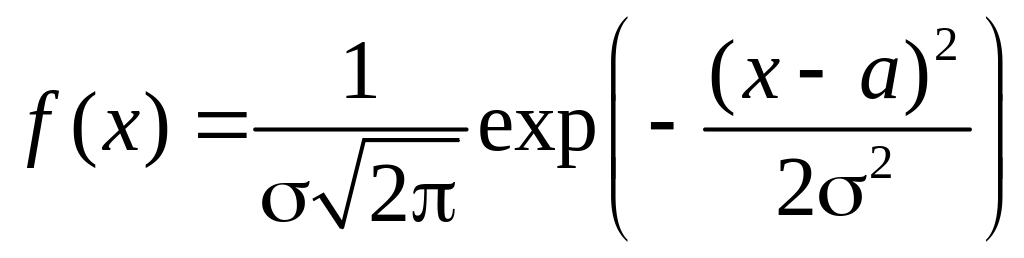Перевіримо виконання умови нормування. Знайдемо:

.

Тут скористалися інтегралом Пуассона (див. п. 1.16):

.

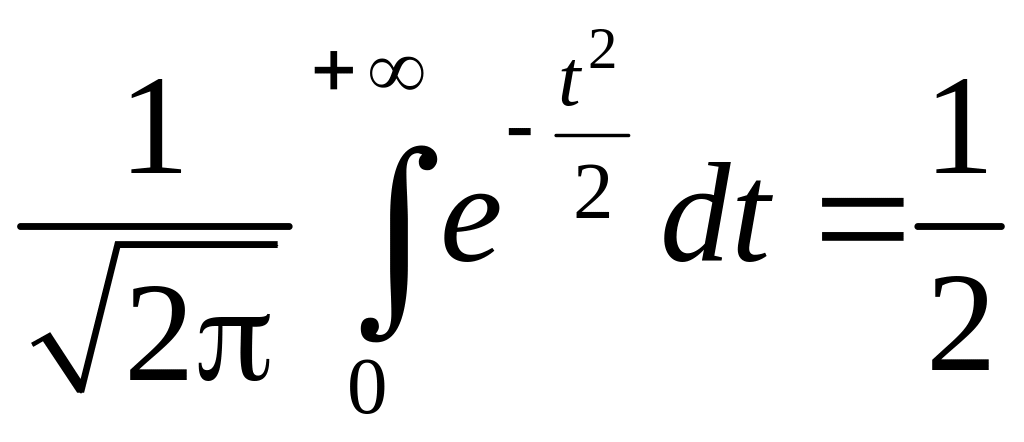Знайдемо числові характеристики нормального розподілу. Почнемо з математичного сподівання:

.

Перший з інтегралів останньої суми є інтегралом у симетричних межах від непарної функції, отже він дорівнює нулю. Таким чином:

(знову на підставі інтеграла Пуассона). Отже математичне сподівання нормального розподілу дорівнює параметру .

Знайдемо дисперсію. Цього разу користуємось загальною формулою для дисперсії, а не «спрощеною».

.

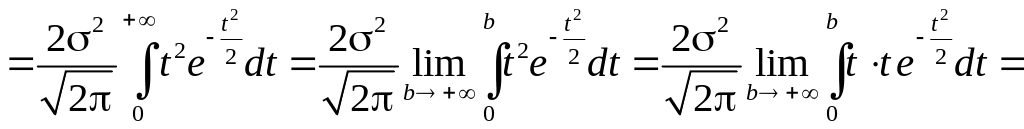
Тут скористалися тим, що

, та інтегралом Пуассона. Таким чином:

, тобто дисперсія нормального розподілу дорівнює . Отже середньоквадратичне відхилення нормального розподілу дорівнює параметру :

.

Водночас ми встановили ймовірнісний зміст параметрів і нормального розподілу. Параметр – математичне сподівання цього розподілу, а параметр – середньоквадратичне відхилення.

Означення. Якщо НВВ розподілена нормально з параметрами і , то величина називається нормованою.

Щільність розподілу нормованої нормальної величини:

.

Легко помітити, що – диференціальна функція Лапласа (див. п. 1.15).

Функція розподілу нормованої величини має вигляд:

.

Її значення можна знайти, користуючись таблицями інтегральної функції Лапласа (див. п. 1.16). Дійсно:

.

Тут скористалися тим, що

(інтеграл Пуассона).

Наприклад: .

Нехай – нормальна випадкова величина з довільними параметрами і . Розглянемо НВВ:

.

Ця величина також розподілена нормально. Покажемо, що вона є нормованою. Дійсно:

;

, отже .

Функція розподілу нормальної випадкової величини з довільними і виражається через функцію за формулою:

.

Дійсно,

.

Для відповідних щільностей розподілів маємо:

.

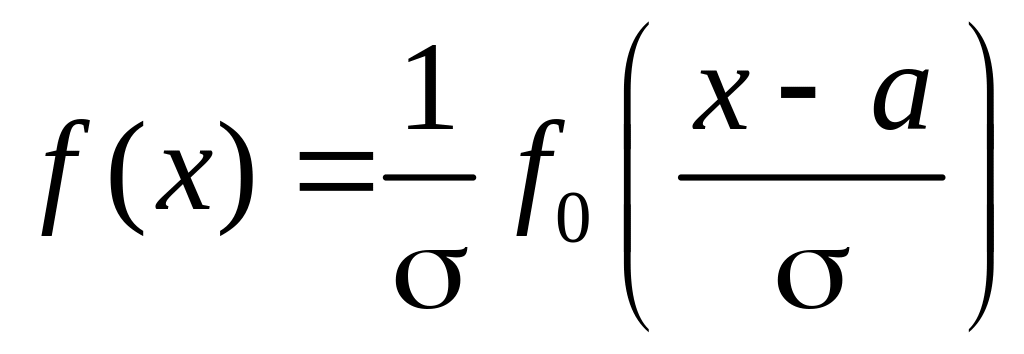2.25. Нормальна крива та вплив параметрів нормального розподілу на її форму.

Означення. Нормальною кривою (або кривою Гауса) називається графік щільності нормального розподілу, тобто функції:

.

Для побудови цього графіку розглянемо спочатку випадок , тобто функцію

.

Функція визначена на всій числовій прямій. Ця функція приймає тільки додатні значення, і вона парна. Тому достатньо дослідити її поведінку лише при .

Маємо:

, отже вісь є горизонтальною асимптотою графіка функції.

Дослідимо функцію на проміжки монотонності та точки екстремуму. Знайдемо:

.

Звідси випливає, що при , тобто функція при є спадною. У точці функція має максимум, який дорівнює .

Дослідимо функцію на проміжки опуклості та вгнутості та точки перегину. Знайдемо:

.

Звідси випливає, що на інтервалі виконано: при ; при ; при . Отже функція є опуклою при і вгнутою при . Точка є точкою перегину.

Таким чином, внаслідок парності графік функції має вигляд:

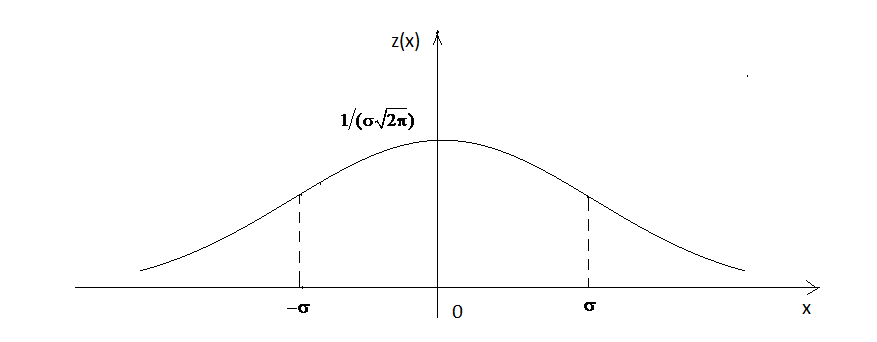
Рис. 26.

Графік функції можна отримати з графіка функції паралельним зсувом вздовж осі на одиниць вправо, якщо , і на одиниць вліво, якщо (рис. 27). Цей графік й є нормальна крива або крива Гауса. Він симетричний відносно прямої . Як ми знаємо, вже з цього випливає, що параметр є математичним сподіванням нормального розподілу.

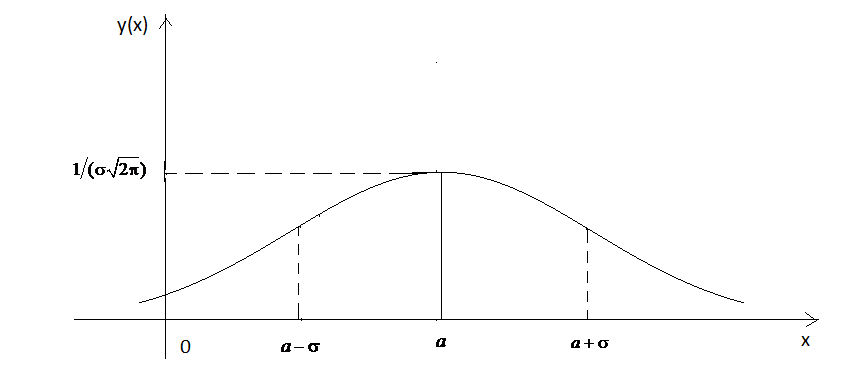
Рис. 27.

З’ясуємо, як впливають на форму та розташування кривої Гауса зміна параметрів і нормального розподілу. Зміна параметру приводить лише до паралельного зсуву кривої вздовж осі без зміни форми цієї кривої. А ось якщо змінюється параметр , ситуація інша. Розглянемо границі

, .

Таким чином при зменшенні параметра максимум функції збільшується, а при збільшенні цей максимум зменшується. Сама крива Гауса при зменшенні стає більш «гостровершинною», розтягується вздовж вертикальної прямої . При збільшенні крива стає більш пологою, стискається до осі (рис. 28).

Рис. 28.