2.23. Показниковий закон надійності.

Нехай є деякий технічний елемент (наприклад, комп’ютер), який працює на протязі деякого проміжку часу. Але за цей час може відбутися відмова цього елементу, причому завчасно момент відмови невідомо. Позначимо як неперервну випадкову величину – час безвідмовної роботи елементу. Тоді подія полягає в тому, що за час відбулася відмова елементу. А ймовірність цієї події є функцією розподілу НВВ : . Отже ймовірність безвідмовної роботи елементу на протязі часу : .

Означення. Функцією надійності називається функція, що визначає ймовірність безвідмовної роботи елементу на протязі часу :

.

Як правило, час безвідмовної роботи елементу має показників розподіл:

.

Тоді функція надійності:

.

Показниковим законом надійності називається функція надійності, яка визначається рівністю:

, де – інтенсивність відмов.

Приклад. Відбувається випробування 3-х елементів, що працюють незалежно один від одного. Час безвідмовної праці елементів розподілено за показниковим законом: для 1-го елемента щільність розподілу , для 2-го – , для 3-го – . Знайти ймовірність того, що в інтервалі часу відмовить хоча б один елемент.

Знайдемо функцію розподілу для кожного елемента: ; ; .

Ймовірність того, що за інтервал часу 1-й елемент буде працювати безвідмовно, дорівнює:

.

Для 2-го та 3-го елементів відповідні ймовірності дорівнюють:

,

.

Тоді ймовірність того, що за інтервал часу відмовить хоча б один елемент, дорівнює:

.

Показниковий закон надійності має наступну важливу властивість.

Теорема. Ймовірність безвідмовної роботи елемента на інтервалі часу тривалістю не залежить від часу попередньої роботи до початку інтервалу, що розглядається, а залежить тільки від тривалості часу (при заданої інтенсивності відмов ).

Доведення. Нехай подія – безвідмовна робота елемента на інтервалі тривалістю . Подія – безвідмовна робота елемента на інтервалі тривалістю . Тоді – безвідмовна робота елемента на інтервалі тривалістю .

Знайдемо:

, .

Знайдемо умовну ймовірність того, що елемент працюватиме безвідмовно на інтервалі за умови, що він вже працював безвідмовно на попередньому інтервалі :

.

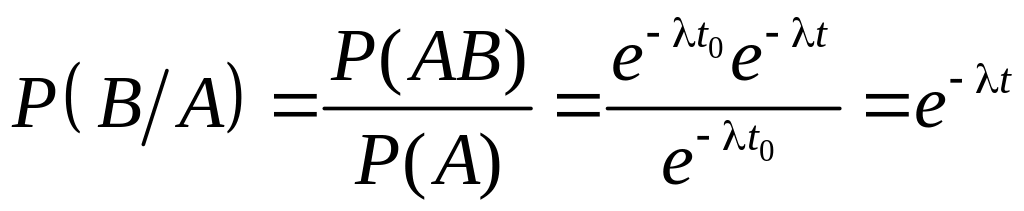Таким чином ймовірність не залежить від , а залежить тільки від . Це й означає, що час праці на попередньому інтервалі не впливає на ймовірність безвідмовної праці на наступному інтервалі, яка залежить тільки від тривалості цього наступного інтервалу.

Зауваження. При доведенні цієї теореми ми суттєво скористалися тим, що закон надійності саме показниковий. Можна довести й обернене твердження, а саме, якщо ймовірність безвідмовної роботи елемента на деякому інтервалі часу не залежить від його роботи на попередніх інтервалах часу, то закон надійності має показниковий розподіл.