2.21. Рівномірний розподіл.

При розв’язанні практичних задач доводиться мати справу з різними розподілами НВВ. Щільності розподілів називають також законами розподілів. Тут ми розглянемо рівномірний розподіл.

Означення. НВВ називається розподіленою рівномірно на відрізку , якщо її щільність розподілу має вигляд:

Тут – стала. Рівномірно розподілені величини зустрічаються досить часто, це величини, які з однаковою ймовірністю можуть прийняти будь яке значення з деякого відрізку. Наприклад, під час контрольного опиту на уроці учень може бути викликаний вчителем у будь яку мить уроку. Можна сказати, що момент часу виклику певного учня є НВВ, рівномірно розподіленою на відрізку (45 хвилин продовжується урок).

Оскільки щільність розподілу відмінна від нуля лише на відрізку , то наша випадкова величина може приймати свої значення лише з цього відрізку. Визначимо сталу , для чого скористаємось Властивістю 3 щільності розподілу:

.

Звідси маємо:

, отже

.

Таким чином, уточнена щільність розподілу має вигляд:

Графік щільності наведено на рис. 22.

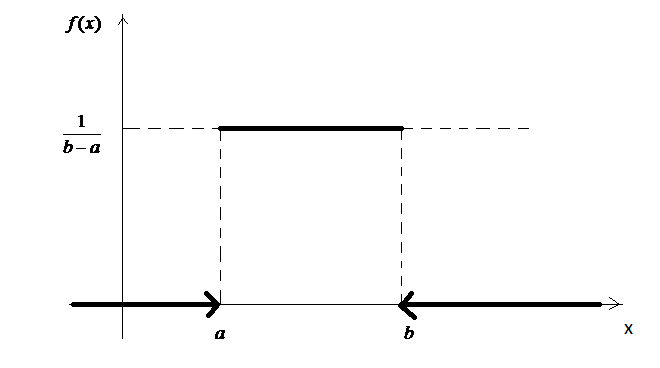
Рис. 22.

Побудуємо тепер функцію розподілу. Оскільки наша випадкова величина приймає свої значення лише на відрізку , то, користуючись Властивістю 4 функції розподілу (див. п. 2.15), можна записати, що при , і при . Знайдемо при :

.

Отже

Графік функції наведено на рис. 23.

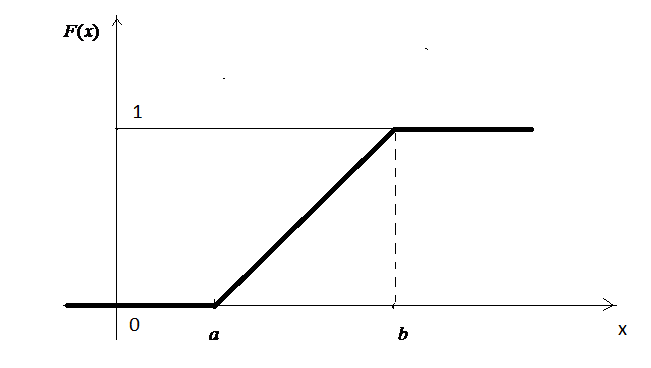
Рис. 23.

Знайдемо тепер числові характеристики рівномірно розподіленої величини . Почнемо з математичного сподівання.

.

Тобто математичне сподівання рівномірного розподілу – це середня точка відрізку . Взагалі, якщо розподіл такий, що графік його щільності симетричний відносно прямої , то математичне сподівання розподілу дорівнює .

Знайдемо дисперсію:

.

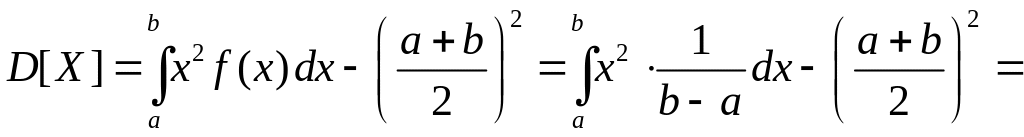
Тепер середньоквадратичне відхилення:

.

Приклад. НВВ розподілена рівномірно на відрізку . Побудувати функцію розподілу, знайти математичне сподівання, дисперсію, середньоквадратичне відхилення.

Щільність розподілу має вигляд:

Функція розподілу:

За формулами, що отримано вище, маємо:

.

2.22. Показниковий розподіл.

Означення. НВВ називається розподіленою за показниковим (експоненціальним) законом з параметром , якщо її щільність розподілу має вигляд:

Графік щільності наведено на рис. 24.

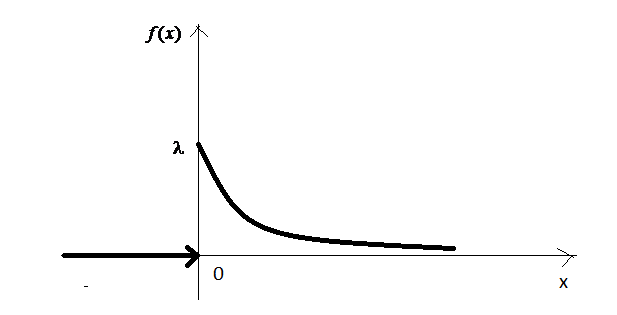
Рис. 24.

Така щільність показує, що величина може приймати лише значення з півінтервалу , причому ці значення групуються головним чином біля початку координат, а при віддаленні від нього ймовірність появи цих значень швидко спадає.

Показниковий розподіл часто використовується для опису інтервалів між послідовними рідкими подіями, наприклад, між відвідуваннями непопулярних сайтів.

Перевіримо виконання умови нормування. Знайдемо:

(на підставі того, що ).

Знайдемо функцію розподілу. При маємо:

.

При :

.

Отже

Графік функції наведено на рис. 25.

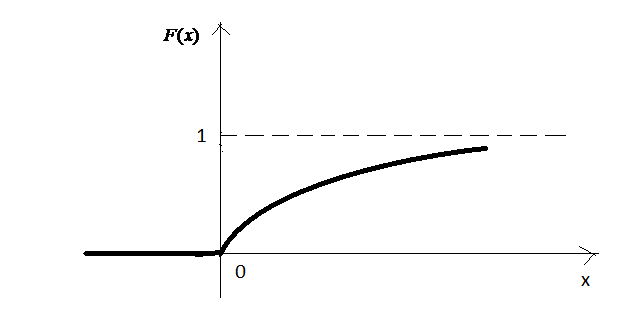
Рис. 25.

Знаючи , знайдемо ймовірність потрапляння НВВ в інтервал (припускаємо, що ):

. (*)

Приклад. НВВ розподілена за показниковим законом з щільністю:

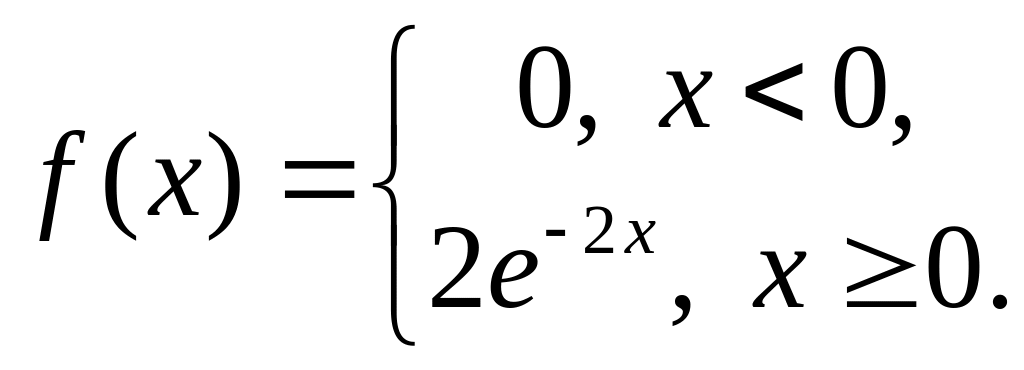
Знайти ймовірність того, що внаслідок випробування величина потрапить в інтервал .

За умовою . За формулою (*):

.

Знайдемо числові характеристики показникового розподілу. Почнемо з математичного сподівання. Інтегруючи за частинами, дістанемо:

.

Оскільки , і за правилом Лопіталя

, то

.

Таким чином математичне сподівання показникового розподілу дорівнює величині, оберненій параметру .

Знайдемо дисперсію за формулою:

.

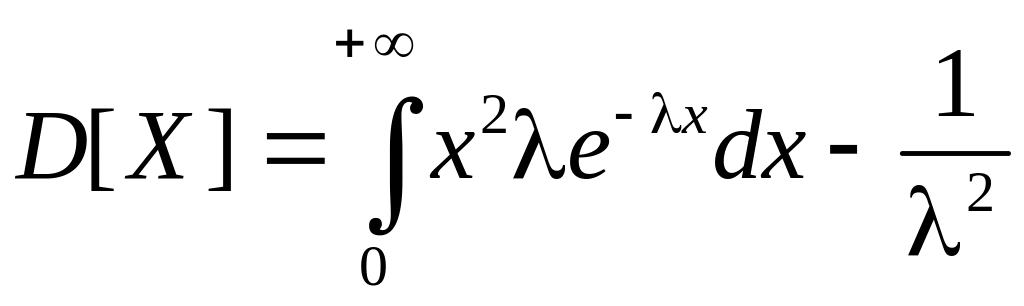Інтегруючи за частинами, дістанемо:

.

Оскільки

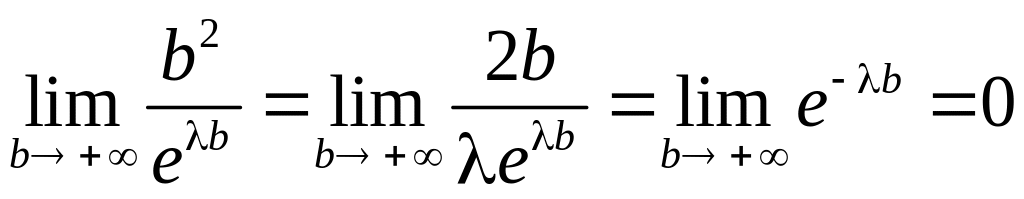, то

.

А тоді

.

Тепер знайдемо середньоквадратичне відхилення:

, тобто математичне сподівання та середньоквадратичне відхилення показникового розподілу співпадають і обернені за величиною параметру .

Приклад. Знайти дисперсію та середньоквадратичне відхилення показникового розподілу, яке задано інтегральною функцією:

.

Параметр дорівнює 0,4, тому

;

;

.