2.16. Функція розподілу дискретної випадкової величини.

Функцію розподілу можна будувати не тільки для неперервної випадкової величини, але й для дискретної.

Приклад 1. Побудувати функцію розподілу ДВВ , яку задано законом розподілу:

	3	4	7	10
	0,2	0,1	0,4	0,3

Розіб’ємо числову пряму на інтервали, межі яких визначаються значеннями ДВВ , і побудуємо функцію розподілу на кожному інтервалі окремо.

а ) : (адже значень, менших 3, величина не приймає);

б) : (адже у цьому випадку є лише єдине значення величини , яке менше, ніж , це );

в) :

(адже у цьому випадку є два значення величини , які менші, ніж , це та );

г) :

(три значення величини , які менші, ніж , це , , );

д) : (тепер всі значення величини є меншими, ніж ).

Графік функції зображено на рис. 20.

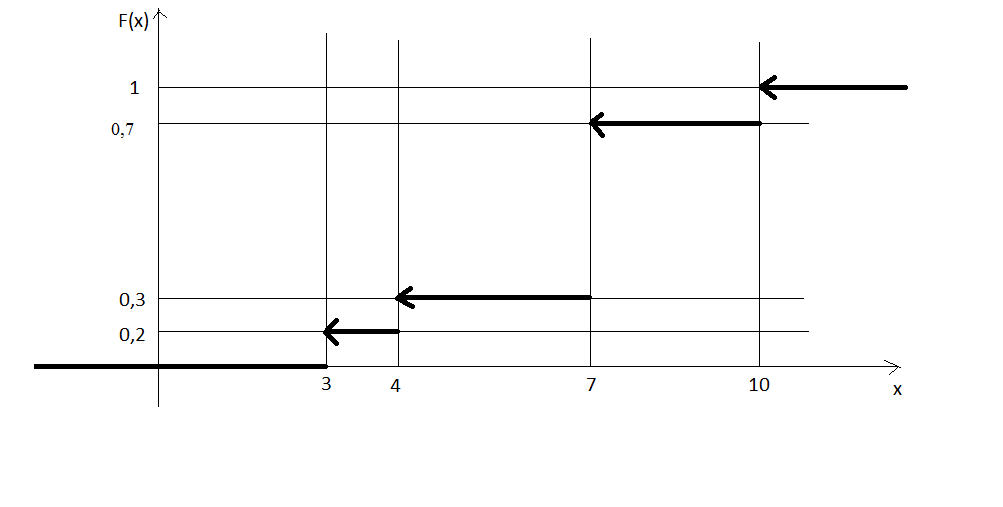
Рис. 20.

Цей графік характерний взагалі для функції розподілу ДВВ. На відміну від функції розподілу НВВ, для ДВВ функція розподілу не є неперервною: вона кусково-неперервна та кусково-стала. В точках, які відповідають значенням випадкової величини, ця функція є неперервною зліва, а справа – розрив I роду (це показується стрілками). Для знаходження значень функції розподілу на кожному інтервалі, очевидно, треба знайти суму ймовірностей значень випадкової величини, що лежать зліва від цього інтервалу.

Приклад 2. Монета кидається до першої появи герба. Побудувати функцію розподілу числа кидань.

Число кидань монети розподілено за геометричним законом (див. п. 2.13):

	1	2	3

Розбиваємо числову пряму на інтервали, що визначаються значеннями випадкової величини (цього разу кількість інтервалів буде нескінченною), і будуємо функцію розподілу на кожному інтервалі окремо:

: ;

: ;

: ;

: ;

…

: ;

…

2.17. Щільність розподілу неперервної випадкової величини.

Нехай задано НВВ , і – її функція розподілу.

Означення. Щільністю розподілу НВВ називається функція

.

Таким чином функція є первісною для функції .

Приклад. Нехай функція розподілу НВВ має вигляд:

.

Знайти щільність розподілу.

Маємо:

.

Теорема. Якщо – НВВ, і – її щільність розподілу, то

.

Доведення. Використовуючи рівність (*) (п. 2.15) і наслідок з Властивості 3 функції розподілу, маємо:

.

За формулою Ньютона – Лейбніца:

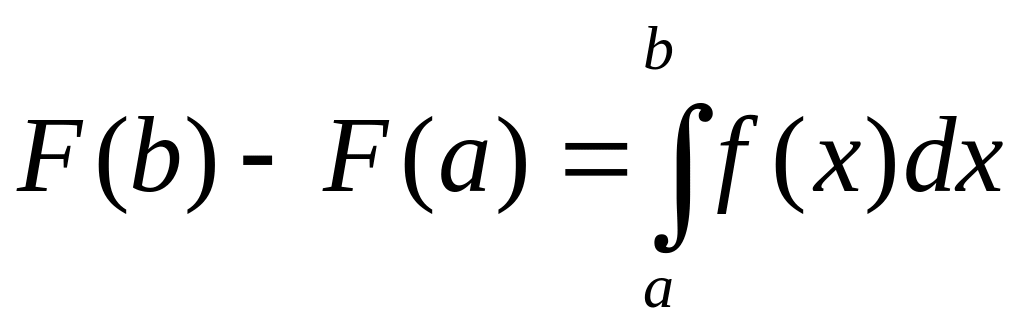, звідки й випливає твердження теореми.

З геометричної точки зору це означає, що ймовірність того, що НВВ внаслідок випробування прийме значення, що належить інтервалу , дорівнює площі криволінійної трапеції, яка обмежена віссю , графіком функції і прямими , (рис. 21).

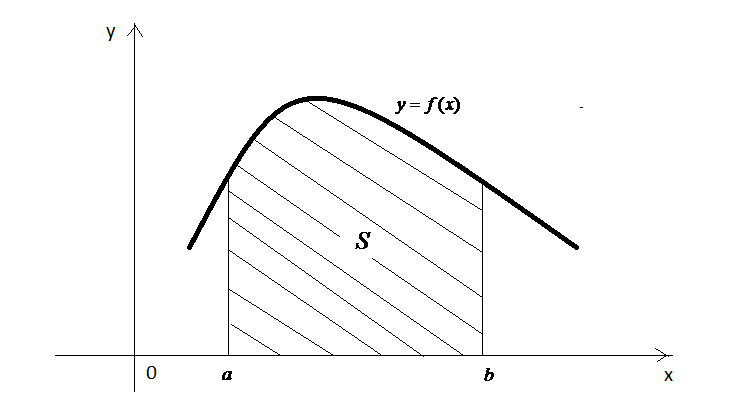
Рис. 21.

.

Висота графіка щільності на певних ділянках числової прямої показує густину групування значень випадкової величини на цих ділянках. Найбільша густина буде там, де більша висота графіка (тобто більше величина щільності розподілу, більше ймовірність того, що внаслідок випробування випадкова величина прийме значення саме з цієї ділянки), а де висота графіка мала, там й густина значень також незначна. На тих ділянках, де щільність нульова, взагалі нема можливих значень випадкової величини.

Приклад. Задано щільність розподілу НВВ :

Знайти .

Згідно з теоремою маємо:

.

Наслідок. Якщо – функція розподілу НВВ , а – щільність розподілу цієї величини, то

.

Доведення. За означенням функції розподілу маємо:

.

Внаслідок рівності і цього Наслідку, функцію іноді називають диференціальною функцією розподілу, а функцію – інтегральною функцією розподілу.

Приклад. Задано щільність розподілу НВВ :

Знайти інтегральну функцію розподілу.

Оскільки щільність розподілу задано різними виразами на різних інтервалах, то й функцію розподілу шукатимемо на кожному інтервалі окремо.

1). :

.

2). :

.

3). :

.

Отже

Ці обчислення можна спростити, якщо скористатися тим, що щільність на 1-му та 3-му інтервалах дорівнює нулю, отже випадкова величина не приймає значення з цих інтервалів, а тоді згідно з Властивістю 4 функції розподілу (див. п. 2.15), на 1-му інтервалі функція дорівнює нулю, а на 3-му – одиниці.