1.8. Умовна ймовірність. Ймовірність добутку подій.
Означення. Умовною ймовірністю події за умови називається ймовірність події , яку обчислено за умови, що подія вже відбулася.
Позначається умовна
ймовірність:
,
або
.
Приклад.
В урні 10 куль – 6 білих та 4 чорних.
Навмання одна за одною з урни виймаються
кулі та відкладаються, тобто в урну не
повертаються. Нехай подія
–
-а
куля, що дістали, біла, подія
–
-а
куля, що дістали, чорна. Знайти наступні
ймовірності:
,
,
,
,
,
,
.
Маємо:
;
;
(після 1-го виймання залишилося 9 куль,
серед них 5 білих);
(після 1-го виймання залишилося 9 куль,
серед них 6 білих);
(після 1-го виймання залишилося 9 куль,
серед них 4 чорних);
(після 1-го виймання залишилося 9 куль,
серед них 3 чорних);
(після 2-го виймання залишилося 8 куль,
серед них 4 білих).
Теорема. Умовна ймовірність події за умови дорівнює ймовірності події , поділеної на ймовірність події :
.
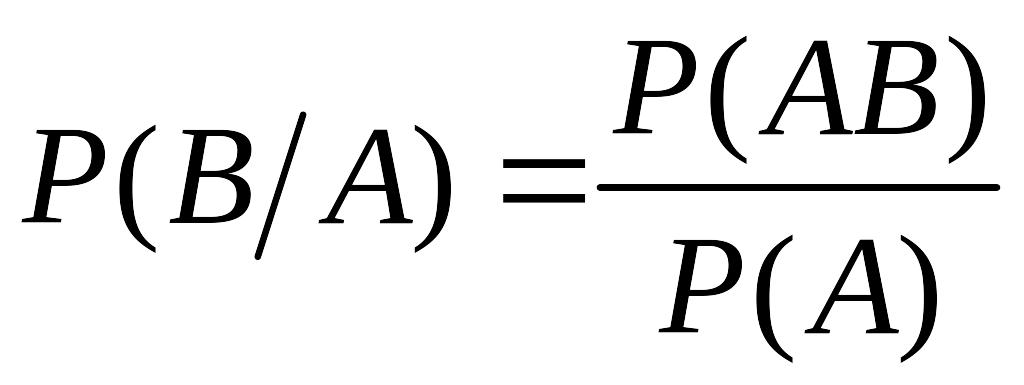Доведення. Нехай – число всіх рівноможливих наслідків випробування, – число наслідків, які сприяють події , – число наслідків, які сприяють події , – число наслідків, які сприяють події . Тоді
,
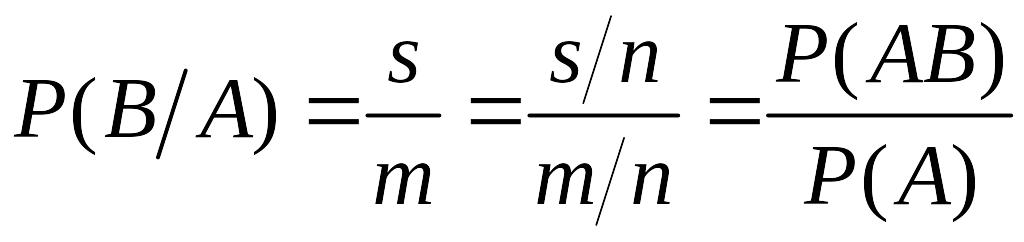що й треба було довести.
Наслідок. Ймовірність добутку подій і , тобто події , дорівнює ймовірності події , помноженої на умовну ймовірність події за умови :
.
(*)
Приклад. Студент при підготовці до заліку вивчив 25 питань з 30, що були у програмі. Знайти ймовірність того, що він відповість на 2 поспіль питання, що запропоновано викладачем.
Позначимо:
– подія, що полягає в тому, що студент
відповість на перше питання,
– подія, яка полягає в тому, що він
відповість на друге питання. Тоді подія,
що нас цікавить, це
.
Маємо:
.
Зауваження 1. Застосовуючи формулу (*) до події , дістанемо:
.
Але, оскільки
,
то
,
тобто
.
(**)
Зауваження 2.
Формула (*) легко узагальнюється на
випадок добутку декількох подій.
Наприклад, для трьох подій
маємо:
.
Означення. Подія називається незалежною від події , якщо поява події не змінює ймовірності події , тобто, якщо умовна ймовірність події за умови дорівнює безумовній ймовірності події :
.
Підставляючи це співвідношення до формули (**), дістанемо:
,
звідки
,
а це означає, що й подія
не залежить від події
.
Отже, якщо подія
не залежить від події
,
то й подія
не залежить від події
.
Тобто властивість незалежності події
є взаємною.
Для незалежних подій і формула (*) набуває вигляду:
,
(***) тобто ймовірність
сумісної появи двох незалежних подій
дорівнює добутку їх ймовірностей.
Рівність (***) приймається також в якості означення незалежних подій.
Означення. Дві події називаються незалежними, якщо ймовірність їх сумісної появи дорівнює добутку ймовірностей цих подій; в протилежному випадку події називаються залежними.
Приклад. Два стрілка стріляють по одній цілі по одному разу. Першій стрілок влучає в ціль з ймовірністю 0,8, а другий – з ймовірністю 0,6. Знайти ймовірність того, що обидва стрілки влучать в ціль.
Нехай подія полягає в тому, що в ціль влучив перший стрілок, подія – в ціль влучив другий стрілок. Оскільки жодна з цих подій ніяк не впливає на ймовірність іншої (стрілки влучають або не влучають в ціль повністю незалежно один від одного), то події і незалежні, отже згідно з (***):
.
Означення.
Декілька подій
називаються попарно
незалежними, якщо кожні
два з них незалежні.
Означення. Декілька подій називаються незалежними в сукупності, якщо вони попарно незалежні, і, крім того, кожна з цих подій є незалежною зі всіма можливими добутками решти цих подій.
Наприклад, якщо події
незалежні в сукупності, то незалежними
є події:
і
,
і
,
і
,
і
,
і
,
і
.
Якщо події незалежні в сукупності, то вони є й попарно незалежними. Але зворотне твердження несправедливе, тобто з попарної незалежності подій не випливає, взагалі кажучи, їх незалежність в сукупності.
Приклад.
Нехай в скриньці є 4 кулі – одна червона,
одна синя, одна чорна і одна пофарбована
в усі три ці кольори. Навмання з скриньки
виймається одна куля. Знайдемо ймовірність
того, що вона має червоний колір. Нехай
подія
– куля має червоний колір, подія
– куля має синій колір, подія
– куля має чорний колір. Оскільки
червоний колір мають дві кулі з 4-х, то
.
Аналогічно
,
.
Припустимо тепер, що вийнята куля має
синій колір, тобто подія
вже відбулася. Знайдемо
.
Синій колір мають тільки дві кулі, а з
цих двох червоний має тільки одна. Отже
,
тобто події
і
незалежні. Аналогічно і події
і
,
і
також незалежні. Таким чином, події
є попарно незалежними. Чи є вони
незалежними в сукупності? Знайдемо
.
Синій та чорний колір водночас має
тільки одна куля, вона ж обов’язково
має й червоний колір, отже
,
тобто
.
Отже події
не є незалежними в сукупності.
Теорема. Якщо події незалежні в сукупності, то
.
Доведення.
Розглянемо три події
.
Сумісність подій
рівносильна сумісності подій
і
,
отже
.
Оскільки події незалежні в сукупності, то, зокрема, незалежні події і , а також і . За формулою (***) маємо:
.
Для випадку подій доведення проводиться аналогічно. Зауважимо, що якби події були незалежними не в сукупності, а тільки попарно, то ця теорема не була б справедливою. Дійсно, повертаючись до вищеописаного прикладу з скринькою, де 4 кулі 3-х кольорів, маємо:
,
але в той же час
,
оскільки водночас
всі три кольори має тільки одна куля з
4-х.