
- •Розділ I. Випадкові події.
- •Предмет теорії ймовірностей. Коротка історична довідка.
- •1.2. Випадкові події та дії над ними.
- •1.3. Класичне означення ймовірності події.
- •1.4. Деякі поняття комбінаторики.
- •1.5. Задачі на безпосередній підрахунок ймовірностей.
- •1.6. Статистичне означення ймовірності.
- •1.7. Геометрична ймовірність.
- •1.8. Умовна ймовірність. Ймовірність добутку подій.
- •1.9. Ймовірність суми подій.
- •1.10. Задачі на обчислення ймовірностей суми та добутку подій.
- •1.11. Формула повної ймовірності.
- •1.12. Формули Байєса.
- •1.13. Повторення незалежних випробувань. Формула Бернуллі.
- •1.14. Повторення незалежних випробувань. Формула Пуассона.
- •1.15. Повторення незалежних випробувань. Локальна теорема Муавра – Лапласа.
- •1.16. Повторення незалежних випробувань. Інтегральна теорема Муавра – Лапласа.
- •1.17. Послідовність незалежних випробувань. Найбільш ймовірне число появ події.
1.7. Геометрична ймовірність.
Вище відмічалося, що класичне означення ймовірності має, зокрема, той недолік, що це означення не можна застосувати до випробувань з нескінченною кількістю наслідків. З метою подолання цього недоліку вводять геометричні ймовірності, а саме ймовірності потрапляння точки в деяку суцільну множину точок (частину лінії, площини, простору тощо).
Розглянемо деяку плоску
фігуру
![]() .
І нехай
.
І нехай
![]() – частина цієї фігури (рис. 1).
– частина цієї фігури (рис. 1).
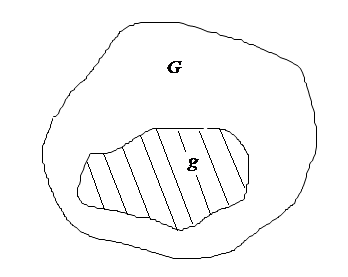
Рис. 1.
Нехай у фігуру випадковим чином потрапляє точка . Ця точка може опинитися в будь якій точці фігури . Треба знайти ймовірність того, що точка потрапить до фігури . При цьому припускається, що ймовірність потрапляння точки в фігуру прямо пропорційна площі цієї фігури.
Нехай
![]() – ймовірність потрапляння точки
у фігуру
.
Тоді
– ймовірність потрапляння точки
у фігуру
.
Тоді
![]() ,
де
,
де
![]() – площа фігури
,
а
– коефіцієнт пропорційності. Зокрема,
фігура
може співпадати зі всією фігурою
,
отже
– площа фігури
,
а
– коефіцієнт пропорційності. Зокрема,
фігура
може співпадати зі всією фігурою
,
отже
![]()
![]() .
З іншого боку, оскільки у фігуру
точка
за умовою потрапляє обов’язково, то
.
З іншого боку, оскільки у фігуру
точка
за умовою потрапляє обов’язково, то
![]() ,
тобто
,
тобто
![]() ,
звідки маємо:
,
звідки маємо:
![]() .
Отже
.
Отже
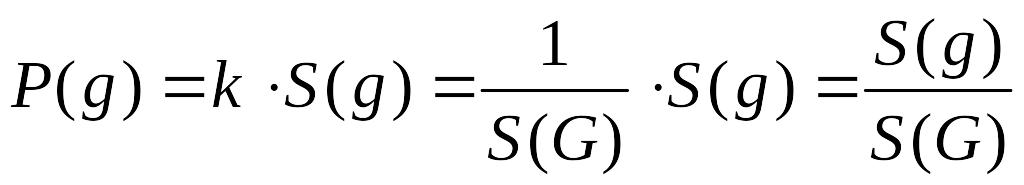 .
.
Якщо фігури
і
розглядаються не на площині, а на лінії,
то замість площі використовуються
довжина. Якщо фігури розглядаються у
тривимірному просторі, то використовується
об’єм. У загальному випадку використовується
термін міра:
![]() .
І таким чином отримуємо формулу:
.
І таким чином отримуємо формулу:
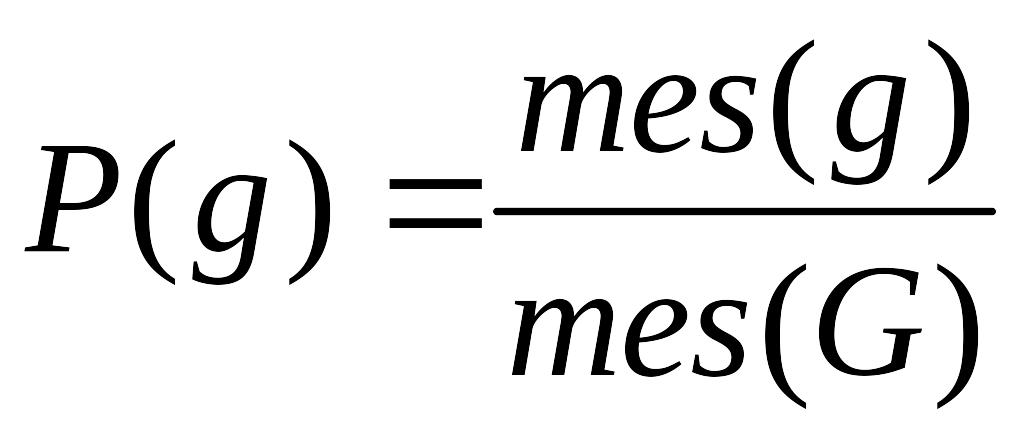 .
.
Ця формула називається формулою геометричної ймовірності.
Приклади.
1. На відрізку довжиною
![]() розташовано менший відрізок довжиною
розташовано менший відрізок довжиною
![]() .
Знайти ймовірність того, що точка, яку
навмання поставлено на більший відрізок,
потрапить також на менший.
.
Знайти ймовірність того, що точка, яку
навмання поставлено на більший відрізок,
потрапить також на менший.
Згідно з формулою геометричної ймовірності маємо:
![]() .
.
2. У круг радіусу
![]() поміщено концентричний з ним круг
радіусу
поміщено концентричний з ним круг
радіусу
![]() .
Знайти ймовірність того, що точка, яку
навмання кинуто в більший круг, потрапить
в кільце, яке утворено між колами цих
кругів (рис. 2).
.
Знайти ймовірність того, що точка, яку
навмання кинуто в більший круг, потрапить
в кільце, яке утворено між колами цих
кругів (рис. 2).
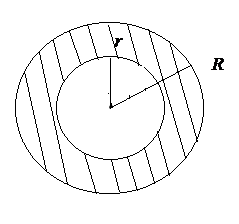
Рис. 2.
Згідно з формулою геометричної ймовірності маємо:
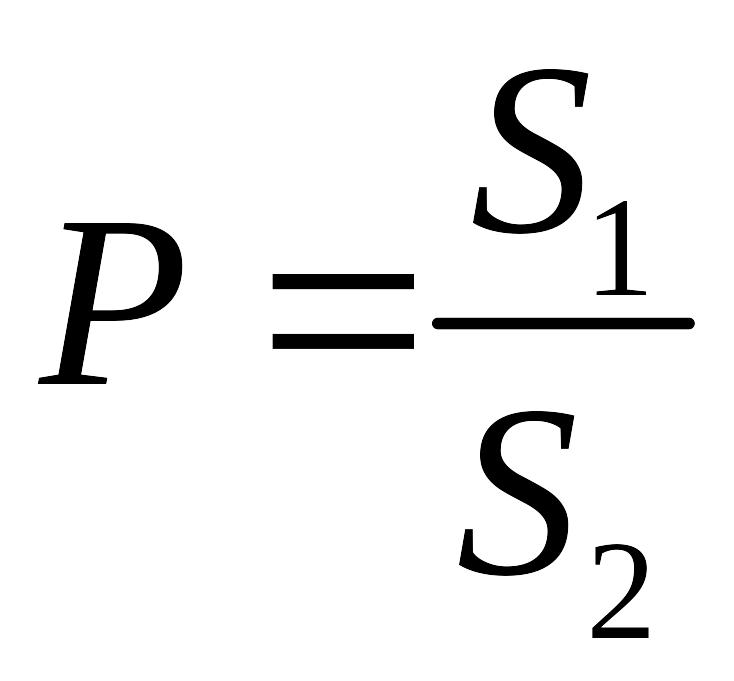 ,
де
,
де
![]() – площа кільця,
– площа кільця,
![]() – площа великого круга. Маємо:
– площа великого круга. Маємо:
![]() ,
,
![]() ,
отже
,
отже
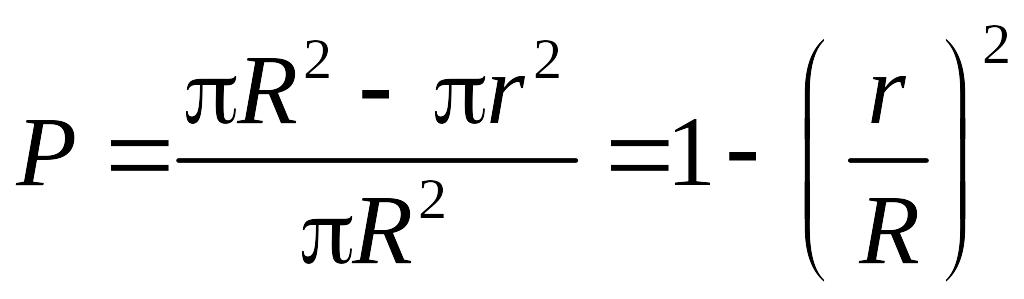 .
.
3. У куб вписано кулю. Знайти ймовірність того, що точка, яку навмання кинуто в куб, потрапить також у кулю.
Згідно з формулою геометричної ймовірності маємо:
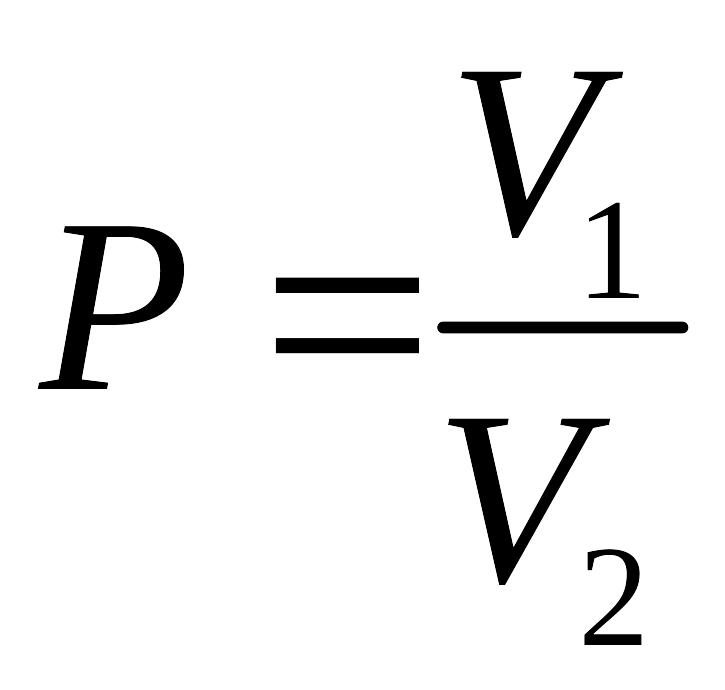 ,
де
,
де
![]() – об’єм кулі,
– об’єм кулі,
![]() – об’єм куба. Нехай
– довжина ребра куба, тоді радіус кулі
– об’єм куба. Нехай
– довжина ребра куба, тоді радіус кулі
![]() .
Отже
.
Отже
![]() ,
,
![]() ,
і таким чином:
,
і таким чином:
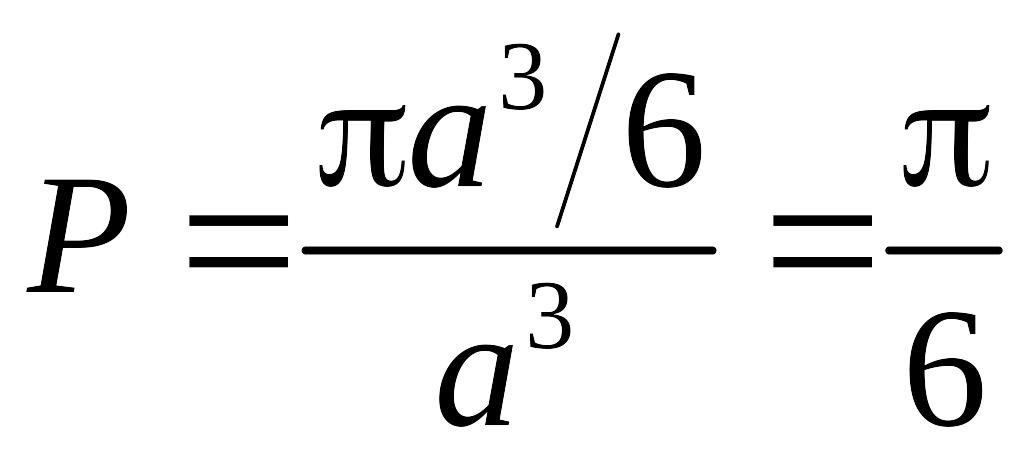 .
.
Ми бачимо, що ця ймовірність не залежить від , тобто розмірів куба.
4. На площину нанесено
сітку квадратів зі стороною
.
На цю площину навмання кинуто монету
радіусу
![]() .
Знайти ймовірність того, що монета не
перетинатиме жодної з сторін квадратів.
.
Знайти ймовірність того, що монета не
перетинатиме жодної з сторін квадратів.
Розглянемо квадрат зі стороною (рис. 3).
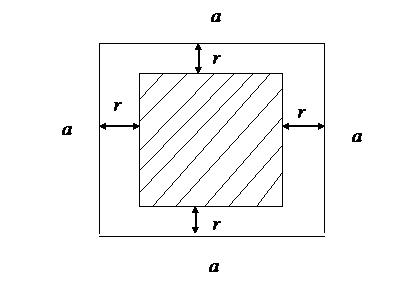
Рис. 3.
Для того, щоб кинута в нього
монета не перетинала жодної з його
сторін, необхідно і достатньо, щоб центр
монети потрапив до розташованого в
ньому меншого квадрату, сторона якого
дорівнює
![]() ,
і ці квадрати мають спільний центр
(точку перетину діагоналей). Таким чином,
ми приходимо до задачі: знайти ймовірність
того, що точка
(центр монети), яка потрапляє до більшого
квадрату, потрапить також у менший
квадрат.
,
і ці квадрати мають спільний центр
(точку перетину діагоналей). Таким чином,
ми приходимо до задачі: знайти ймовірність
того, що точка
(центр монети), яка потрапляє до більшого
квадрату, потрапить також у менший
квадрат.
Маємо:
![]() ,
де
– площа меншого квадрату,
– площа більшого квадрату. Отже:
,
де
– площа меншого квадрату,
– площа більшого квадрату. Отже:
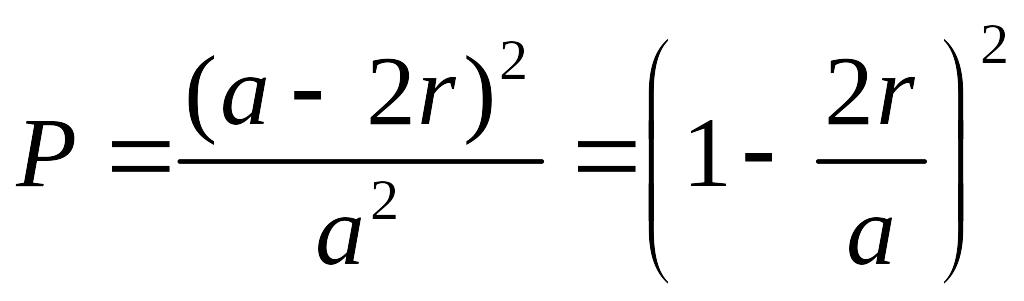 .
.
5. Задача
Бюффона. Площину
розкреслено паралельними прямими,
відстань між двома сусідніми дорівнює
![]() .
На площину навмання кидають відрізок
довжиною
.
На площину навмання кидають відрізок
довжиною
![]() .
Знайти ймовірність того, що цей відрізок
перетинатиме яку-небудь з прямих.
.
Знайти ймовірність того, що цей відрізок
перетинатиме яку-небудь з прямих.
Нехай точка
–
середина відрізку,
![]() – відстань від точки
до найближчої прямої,
– відстань від точки
до найближчої прямої,
![]() – кут, який утворено відрізком з цією
прямою (рис. 4).
– кут, який утворено відрізком з цією
прямою (рис. 4).
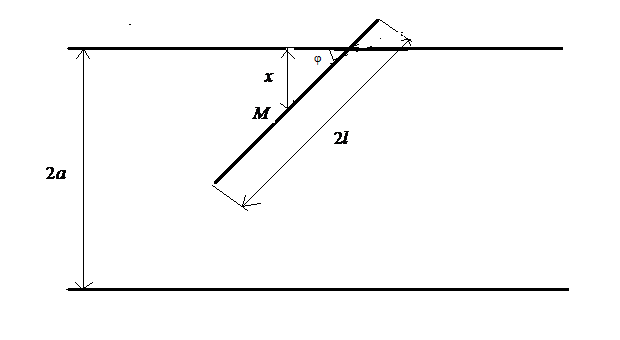
Рис. 4.
Положення відрізку, який
кинуто, повністю визначається заданням
певних значень
і
,
причому
приймає значення від
![]() до
до
![]() ,
а
– від
до
,
а
– від
до
![]() .
Іншими словами точка
може потрапити в будь яку точку
прямокутника зі сторонами
і
.
Таким чином цей прямокутник можна
розглядати як фігуру
,
точками якої є всі можливі положення
точки
.
Очевидно, що площа фігури
дорівнює
.
Іншими словами точка
може потрапити в будь яку точку
прямокутника зі сторонами
і
.
Таким чином цей прямокутник можна
розглядати як фігуру
,
точками якої є всі можливі положення
точки
.
Очевидно, що площа фігури
дорівнює
![]() .
.
Знайдемо тепер фігуру
,
кожна точка якої сприяє події, що нас
цікавить, тобто фігуру, до якої має
потрапити точка
для того, щоб відрізок, який кинуто,
перетинав пряму лінію. З рис. 4 видно, що
відрізок перетинатиме найближчу до
нього пряму тоді і тільки тоді, коли
![]() .
Таким чином, якщо ввести систему координат
.
Таким чином, якщо ввести систему координат
![]() ,
то точка
,
потрапляючи до прямокутника
,
то точка
,
потрапляючи до прямокутника
![]() ,
має потрапити до криволінійної трапеції,
яку обмежено графіком функції
,
має потрапити до криволінійної трапеції,
яку обмежено графіком функції
![]() (рис. 5).
(рис. 5).
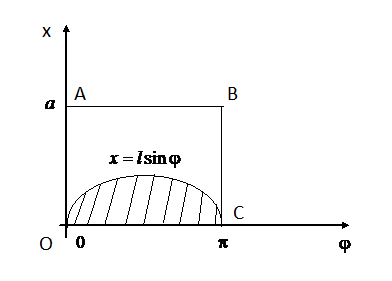
Рис. 5.
Саме цю трапецію можна розглядати як фігуру . Її площа:
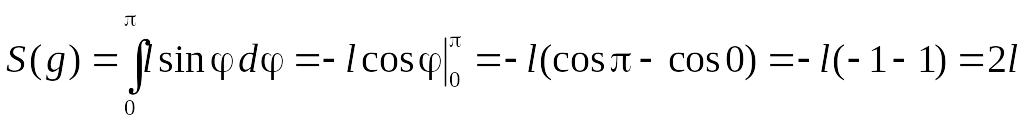 .
.
Отже шукана ймовірність дорівнює:
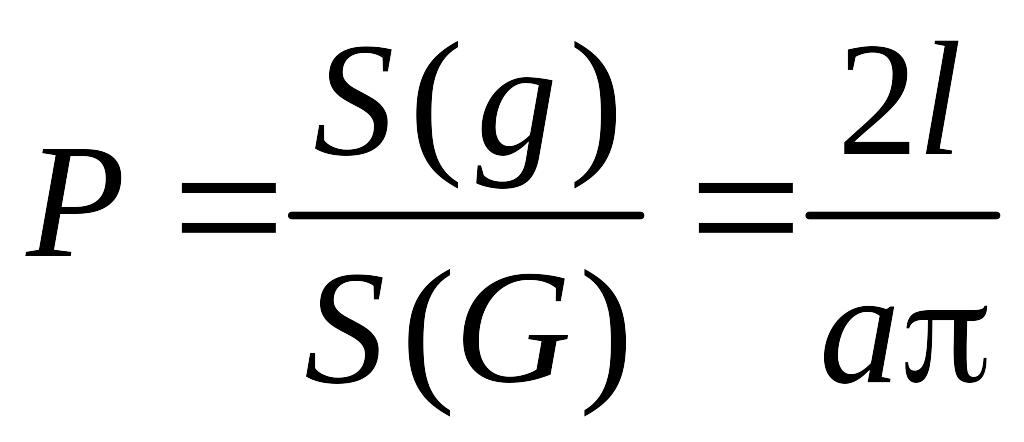 .
.
6. На відрізок
![]() навмання поставлено дві точки, координати
яких
та
навмання поставлено дві точки, координати
яких
та
![]() .
Знайти ймовірність того, що з відрізків,
на які ці точки розбивають відрізок
,
можна побудувати трикутника.
.
Знайти ймовірність того, що з відрізків,
на які ці точки розбивають відрізок
,
можна побудувати трикутника.
Для того, щоб з трьох
відрізків можна було побудувати
трикутника, необхідно і достатньо, щоб
довжина кожного з відрізків була меншою,
ніж сума довжин двох інших. Оскільки
сума довжин всіх трьох відрізків дорівнює
,
то кожен з відрізків за довжиною має
бути меншим, ніж
![]() .
.
Введемо до розгляду
прямокутну систему координат
![]() .
Координати
та
задовольняють подвійні нерівності:
.
Координати
та
задовольняють подвійні нерівності:
![]() .
.
Розглянемо точку
![]() .
Для того, щоб ці нерівності виконувалися,
необхідно і достатньо, щоб точка
потрапила до квадрату
(рис. 6). Таким чином цей квадрат можна
розглядати як фігуру
.
Для того, щоб ці нерівності виконувалися,
необхідно і достатньо, щоб точка
потрапила до квадрату
(рис. 6). Таким чином цей квадрат можна
розглядати як фігуру
![]() ,
до якої обов’язково потрапляє точка
.
Тоді
,
до якої обов’язково потрапляє точка
.
Тоді
![]() .
.
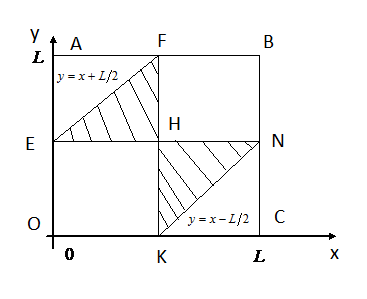
Рис. 6.
Розглянемо два можливі випадки.
1)
![]() :
:
Тоді для здійснення події, що нас цікавить, має бути:
![]() ,
,
або
![]() .
(*)
.
(*)
2)
![]() :
:

У цьому випадку має бути:
![]() .
(**)
.
(**)
Нерівності (*) виконано для
точок трикутника
![]() ,
а нерівності (**) – для точок трикутника
,
а нерівності (**) – для точок трикутника
![]() (рис. 6). Таким чином ці трикутники й є
фігура
,
до якої має потрапити точка
,
щоб відбулася подія, що нас цікавить.
Отже:
(рис. 6). Таким чином ці трикутники й є
фігура
,
до якої має потрапити точка
,
щоб відбулася подія, що нас цікавить.
Отже:
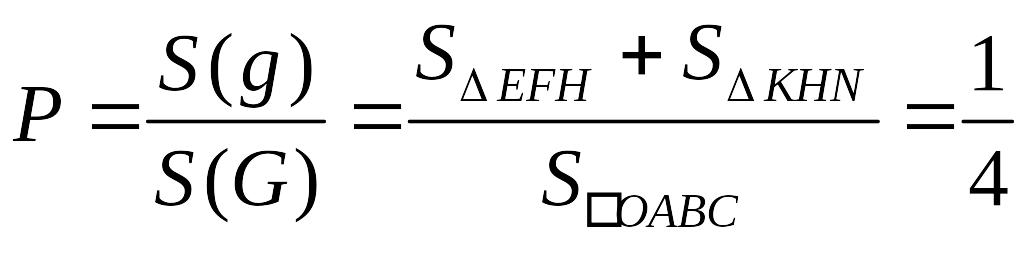 .
.
7. Задача про зустріч. Два студенти домовилися зустрітися в певному місці між 12 та 13 годинами. Той, що прийшов першим, чекає другого на протязі чверті години, після чого уходить. Знайти ймовірність того, що зустріч відбудеться, якщо кожен студент навмання вибирає мить свого приходу.
Нехай – мить приходу одного з студентів, – мить приходу іншого. Оскільки обидва приходи можуть здійснюватися на протязі години, то
![]() .
.
Зустріч відбудеться тоді і тільки тоді, коли буде виконано нерівність:
![]() .
.
Введемо прямокутну систему
координат
і розглянемо квадрат
зі стороною 1 (рис. 7);
![]() .
.
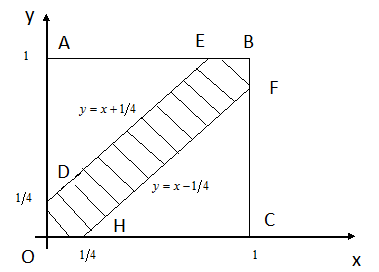
Рис. 7.
Фігура, яка відповідає
останній нерівності, є многокутник
![]() .
Введемо точку
.
Зустріч відбудеться тоді і тільки тоді,
коли точка
,
потрапляючи до квадрату
,
потрапить при цьому до фігури
.
Отже шукана ймовірність:
.
Введемо точку
.
Зустріч відбудеться тоді і тільки тоді,
коли точка
,
потрапляючи до квадрату
,
потрапить при цьому до фігури
.
Отже шукана ймовірність:
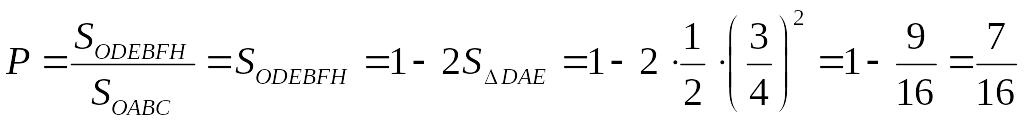 .
.
8. Навмання взято два
додатні числа
![]() ,
кожне з яких не перевищує 2. Знайти
ймовірність того, що їх добуток
,
кожне з яких не перевищує 2. Знайти
ймовірність того, що їх добуток
![]() буде не більше за одиницю, а частка
буде не більше за одиницю, а частка
![]() – не більша, ніж 2.
– не більша, ніж 2.
Введемо прямокутну систему координат . За умовою:
![]() .
.
Подія, що нас цікавить, відбудеться тоді і тільки тоді, коли
![]() ,
,
або
![]() .
.
Розглянемо точку
.
Для здійснення події необхідно і
достатньо, щоб ця точка, потрапляючи до
квадрату
,
потрапила до фігури
![]() (рис. 8).
(рис. 8).
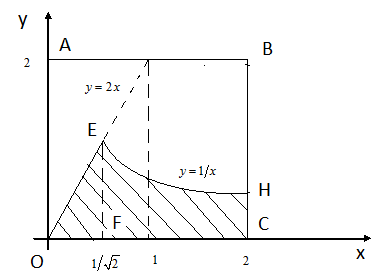
Рис. 8.
Отже шукана ймовірність:
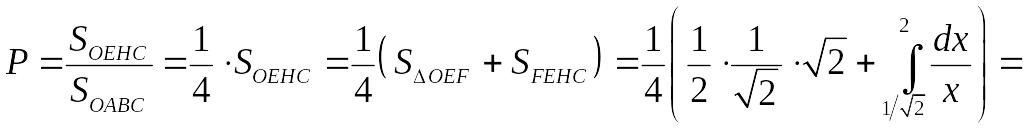
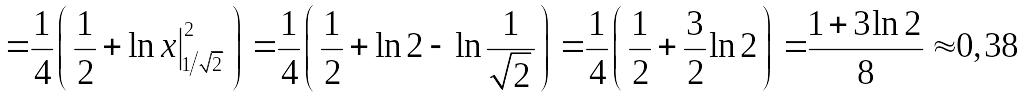 .
.
Помітимо, що задачі 7, 8 за своїм формулюванням, здавалося б, зовсім не геометричні. Але допускають геометричну інтерпретацію, яка й дає можливість використання формули геометричної ймовірності.
