1.5. Задачі на безпосередній підрахунок ймовірностей.

Задача 1. Дитина грає з 5 картками, на яких написано букви О, П, Р, С, Т (на кожній картці одна з цих букв). Яка ймовірність того, що, викладаючи ці картки у випадковому порядку, дитина отримає слово «СПОРТ»?

Скористаємось класичним означенням ймовірності. Загальна кількість всіх рівноможливих елементарних наслідків дорівнює числу переставлень з 5 елементів, тобто . А елементарний наслідок, що сприяє події, тільки один. Таким чином, , , отже

.

Задача 2. Набираючи номер телефону, абонент забув дві останні цифри і набрав їх навмання, пам’ятаючи тільки, що вони непарні та різні. Знайти ймовірність того, що номер набрано правильно.

Позначимо через подію, яка полягає в тому, що набрано потрібні цифри. Ці дві цифри набираються з 5-елементної множини , до того ж суттєвим є порядок їх слідування. Отже число всіх елементарних наслідків дорівнює

.

А сприяє події тільки один наслідок. Таким чином , , отже

.

Задача 3. На одній з кліток шахівниці стоїть біла тура. На якусь іншу клітку навмання ставиться чорна тура. Знайти ймовірність того, що вона не потрапить під бій білої.

Кількість кліток, які контролює тура, не залежить від клітки, на якій вона стоїть – у будь якому випадку вона контролює 14 кліток (7 по горизонталі та 7 по вертикалі). Вільних кліток для чорної тури залишається 63, а з них тих, що не контролюється білою турою – 63-14=49. Отже, , , таким чином:

.

Задача 4. Галя, Марійка, Василь, Петро, Оксана та Наталя прийшли на День народження до Ганни. Всі вони сідають на 7 стільців біля круглого столу. Знайти ймовірність того, що Василь опиниться поряд з Ганною.

Незалежно від стільця, який займе Ганна, вільними залишаються 6 стільців для 6 гостей. Нехай – подія, яка полягає в тому, що Василь опиниться поряд з Ганною. Загальна кількість всіх елементарних наслідків це число способів, якими можуть сісти 6 гостей Ганни, а це є число переставлень з 6 елементів, тобто . Число елементарних наслідків, які сприяють події – . Дійсно, Василь може опинитися ліворуч від Ганни, а може праворуч; у кожному з цих випадків решта гостей можуть сісти будь яким чином, а число таких варіантів 5!. Таким чином

.

Цю задачу можна було б розв’язати і простіше: з 6 місць, що залишилося, поряд з Ганною є тільки 2. Отже шукана ймовірність дорівнює .

Якщо кількість осіб, що сідають біля круглого столу, дорівнює , то аналогічно доводиться, що ймовірність того, що дві конкретні особи опиняться поряд, дорівнює .

Задача 5. Кидаються три монети. Знайти ймовірність того, що «герб» випаде точно на 2 монетах.

Розглянемо всі рівноможливі елементарні наслідки випробування. Випадіння «герба» позначатимемо як Г, а випадіння «решки» – як Р:

ГГГ, ГГР, ГРГ, ГРР, РГГ, РГР, РРГ, РРР.

Таким чином . А елементарних наслідків, що сприяють нашій події – 3: ГГР, ГРГ, РГГ. Тобто , отже

.

Задача 6. Навмання обрана кістка доміно з’явилася не дублем. Знайти ймовірність того, що другу, навмання обрану кістку, можна приставити до першої.

Всього кісток доміно 28, з них дублів 7. Якщо обрана кістка не дубль, наприклад 2-3, то до неї з 27 кісток, що залишилося, можна приставити 12, а саме: 0-2, 1-2, 2-2, 4-2, 5-2, 6-2, 0-3, 1-3, 3-3, 4-3, 5-3, 6-3. Таким чином , , отже

.

Задача 7. 9 мишей біжать до трьох відкритих кліток з кормом. Кожна миша з рівними можливостями може потрапити до будь якої з цих трьох кліток. Знайти ймовірність того, що у кожній клітці опиниться по 3 миші.

Кожна миша має три рівноможливі варіанти потрапляння в клітки. Згідно з основним принципом комбінаторики (див. п. 1.4) всіх варіантів потрапляння всіх 9 мишей буде . Це й буде число всіх елементарних наслідків випробування. Для знаходження числа сприятливих наслідків підрахуємо спочатку кількість способів, якими можна обрати трьох мишей з 9, що є (у першій клітці мають бути три миші). Це буде . З 6 мишей, що залишилося, три мають бути у другій клітці, їх можна обрати способами. І нарешті останні три миші потрапляють в третю клітку вже єдиним способом. Таким чином , , отже

.

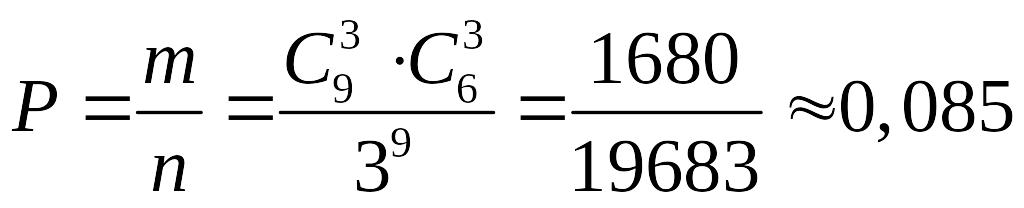Задача 8 (про вибірку). У скриньці містяться 15 куль, з яких 9 білих та 6 чорних. Навмання з скриньки виймаються 10 куль. Знайти ймовірність того, що серед цих 10 рівно 7 білих та 3 чорних.

Загальне число всіх елементарних наслідків дорівнює числу способів, якими можна вибрати 10 куль з 15, тобто . Обчислимо число сприятливих наслідків. До цього числа увійде кількість способів, якими можна вибрати 7 білих куль з 9, що їх є, тобто . На кожен з цих способів прийдеться ще способів, якими можна вибрати 3 чорних кулі з 6, що їх є. Згідно з основним принципом комбінаторики маємо: . Таким чином:

.

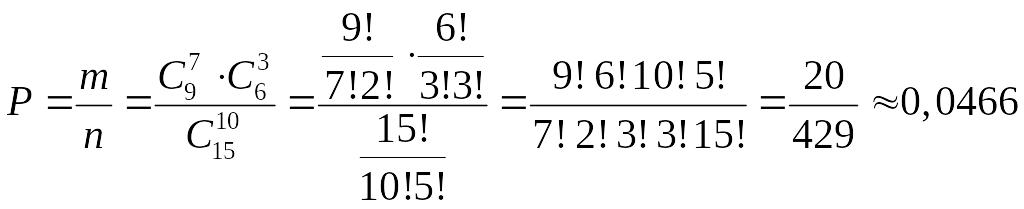Сформулюємо цю задачу та її розв’язок у загальному випадку. Нехай є предметів, з них предметів мають властивість . Навмання вибираються предметів. Знайти ймовірність того, що серед них рівно мають властивість .

Шукана ймовірність дорівнює:

.

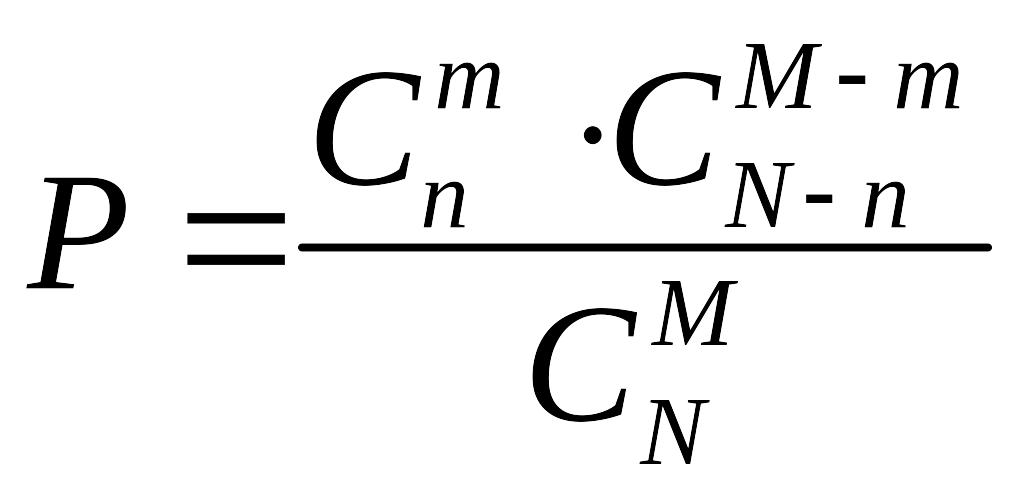Задача 9. З колоди в 52 карти навмання вибираються 3 карти. Знайти ймовірність того, що це будуть трійка, сімка і туз.

Загальна кількість всіх елементарних наслідків дорівнює числу способів, якими можна вибрати 3 карти з 52, тобто . Трійку можна вибрати способами, така ж кількість способів вибору сімки та туза. Згідно з основним принципом комбінаторики . Таким чином:

.

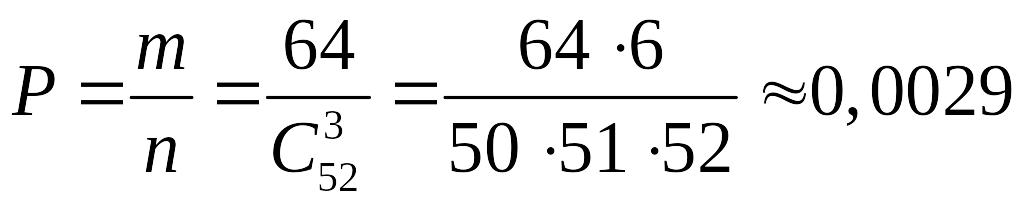Задача 10. Вісім різних книжок поставлено навмання на одній полиці. Знайти ймовірність того, що дві певні книжки опиняться поряд.

Загальна кількість елементарних наслідків дорівнює . Знайдемо число сприятливих наслідків. Дві книжки можна поставити поряд способами, тоді решту книжок можна розставити способами. Крім того маємо 7 можливих положень цих двох книжок вздовж полиці. Отже , і таким чином:

.

Задача 11. Знайти помилку у розв’язанні наступної жартівливої задачі: яка ймовірність, вийшовши в певний час доби на Дерибасівську, зустріти там справжнього живого динозавра?

Розв’язання: всього елементарних наслідків випробування 2 – або зустріти динозавра, або не зустріти. З них сприятливий тільки один – коли зустріти. Отже ймовірність дорівнює (така ж сама, як ймовірність появи герба при киданні монети).