1.4. Деякі поняття комбінаторики.

Для розуміння подальшого матеріалу нам будуть потрібні деякі поняття комбінаторики. Комбінаторика – це розділ математики, який вивчає закономірності, що виникають при розгляді комбінацій, які можна скласти з елементів будь якої природи. Наведемо у якості прикладу типово комбінаторну задачу. У студентській групі навчаються 25 осіб. Треба з них виділити трьох делегатів на студентську конференцію. Скількома способами це можна зробити?

Основним принципом комбінаторики є наступний. Якщо елемент можна вибрати способами, а елемент можна вибрати способами, то пару елементів можна вибрати способами. Наприклад, якщо з пункту до пункту ведуть різних шляхів, а з пункту до пункту ведуть різних шляхів, то з пункту до пункту ведуть різних шляхів.

Під час розв’язування комбінаторних задач доводиться розглядати скінченні множини, що складаються з означених елементів. Залежно від умови задачі розглядаються множини, в яких істотним є або порядок елементів, або їх склад, або перше і друге водночас. Такі скінченні множини (сполуки) дістали назву: переставлення, розміщення, сполучення.

Нехай є множина , яка складається з елементів довільної природи.

Сполуки, що складаються з всіх елементів множини , і відрізняються лише порядком їх перелічення, називаються переставленням цих елементів. Кількість переставлень з елементів позначається .

Приклад. Нехай . Розглянемо всі сполуки, що складаються з всіх елементів множини :

.

Вийшло 6 сполук, таким чином . Легко зрозуміти, що , .

Розглянемо множину, що складається з 4-х елементів: . Знайдемо . Скільки переставлень можна скласти з 4-х елементів? До них увійдуть 6 переставлень, які мають на 1-му місці 1 (відрізняються тільки трьома подальшими елементами), 6 переставлень, які мають на 1-му місці 2, 6 переставлень, які мають на 1-му місці 3, і 6 переставлень, які мають на 1-му місці 4. Всього вийшло переставлень. Тобто . Методом математичної індукції нескладно встановити загальну формулу:

.

Приклад. Скількома способами можна розмістити 12 осіб за столом, біля якого поставлено 12 стільців?

Число способів дорівнює .

Нехай тепер з елементів множини утворюються всі можливі сполуки, що містять елементів ( ). При цьому не враховується порядок перелічення елементів у кожній з сполук. Тобто сполуки, що відрізняються тільки порядком перелічення елементів, не розрізняються. Такі сполуки називають сполученнями з по . Число всіх таких сполук позначається . Можна довести формулу:

.

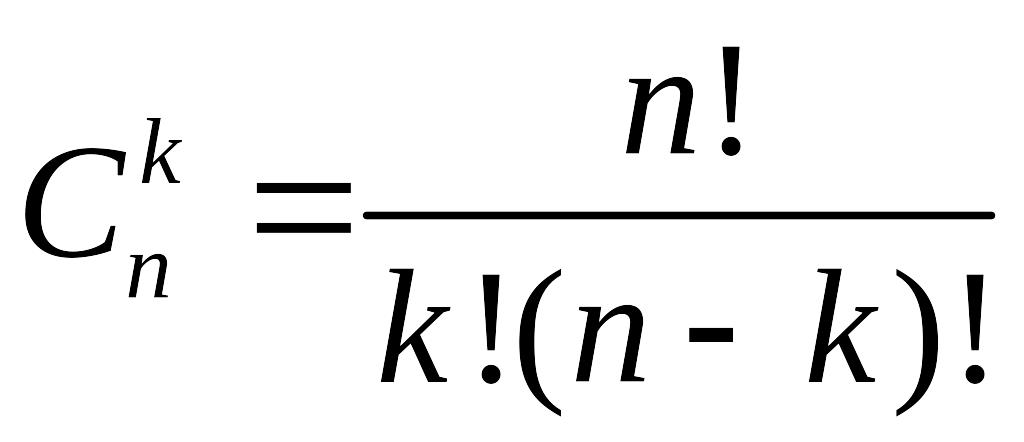Зокрема , . Корисними є також формули:

,

.

Приклад. Студент прийшов до бібліотеки та запросив 7 книжок. А йому можуть видати лише 4 книжки, але будь яких з цих семи. Скількома способами студент може вибрати ці 4 книжки?

Очевидно, що порядок перелічення цих книжок у наборі з 4 книжок не суттєвий, тому шукана кількість способів дорівнює числу сполучень з 7 по 4:

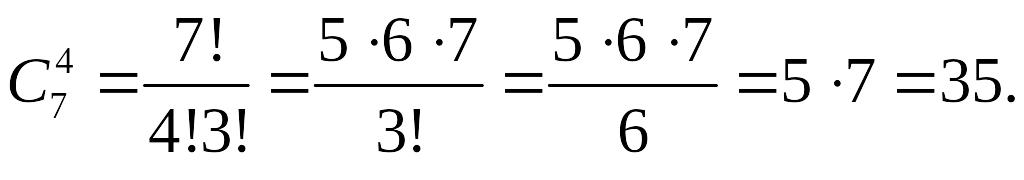
Число сполучень є число способів, якими можна вибрати елементів з множини, що містить елементів.

Будемо тепер з елементів множини знову утворювати всі можливі сполуки, які містять елементів, але цього разу з урахуванням порядку перелічення елементів у кожній з сполук. Тобто сполуки, які складаються з одних і тих же елементів і розрізняються тільки порядком їх перелічення, тепер вважаються різними. Такі сполуки називаються розміщеннями з по . Число всіх таких сполук позначається . Легко зрозуміти, що це число може бути знайдено за формулою:

.

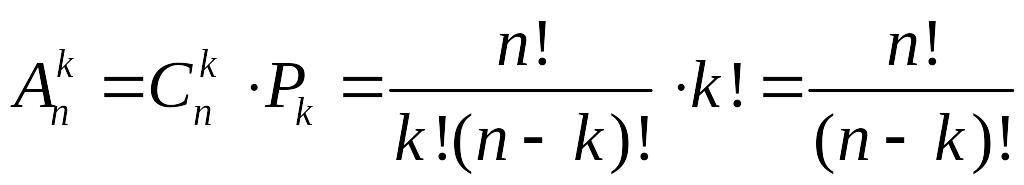Приклад. Скільки існує 6-значних телефонних номерів, всі цифри яких різні?

Очевидно, що ці телефонні номери – сполуки, які утворено з елементів 10-елементної множини, і містять 6 елементів, причому порядок перелічення елементів у кожній сполуці суттєвий (номери, що складаються з одних і тих же цифр, але розрізняються порядком їх слідування, очевидно, різні). Отже число всіх таких номерів є число розміщень з 10 по 6:

.