1.16. Повторення незалежних випробувань. Інтегральна теорема Муавра – Лапласа.

Знову припустимо, що проводиться випробувань ( досить велике), у кожному з яких подія з’являється з ймовірністю . Треба знайти ймовірність того, що число появ події буде у межах від до ( ). Відповідь на це питання дається наближеною формулою, яку ми наводимо без доведення:

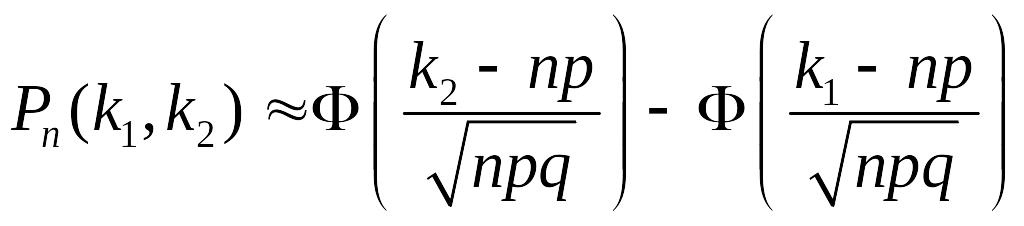, (*) де

.

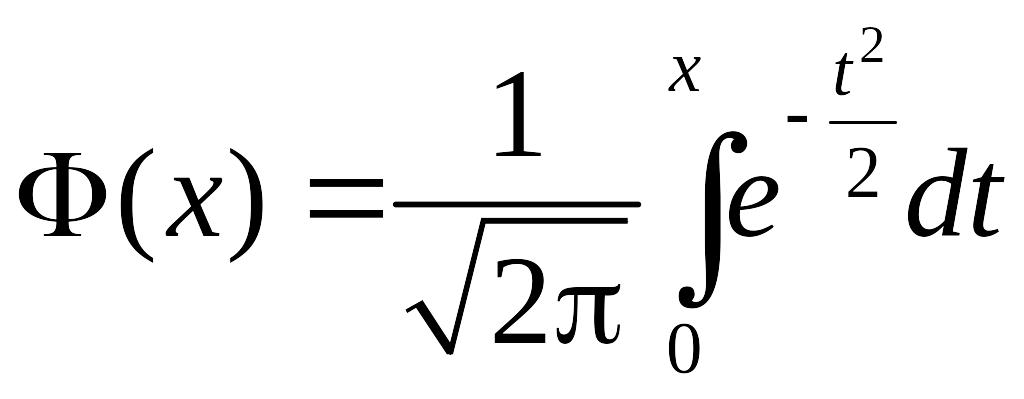Формула (*) називається інтегральною теоремою Муавра – Лапласа, а функція – інтегральною функцією Лапласа (це інтеграл зі змінною верхньою межею від функції ). Дослідимо деякі важливі властивості цієї функції.

1.

.

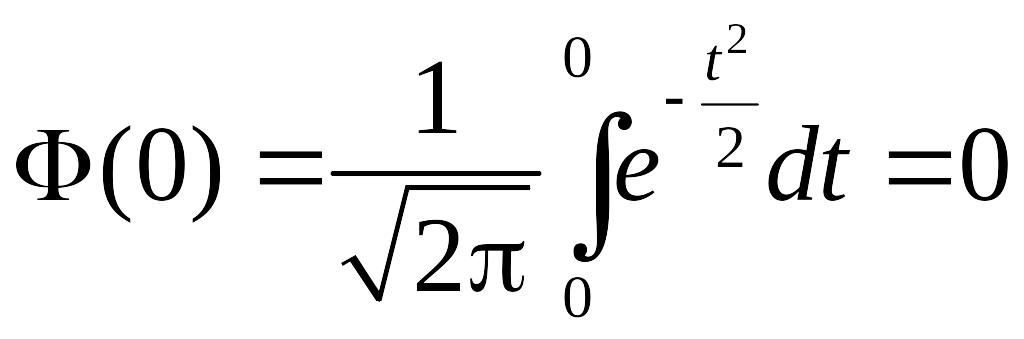2.

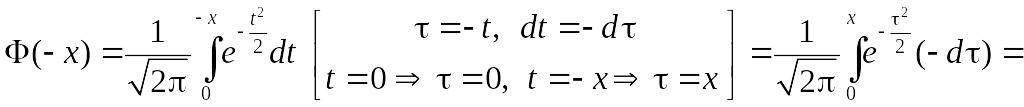
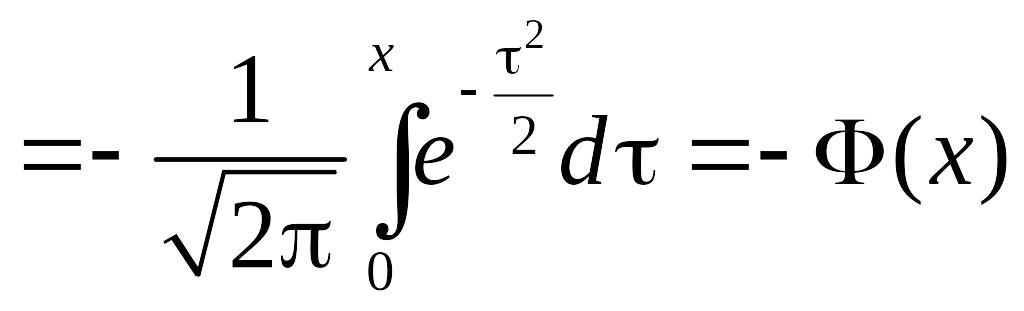, тобто функція непарна.

3. Розглянемо:

.

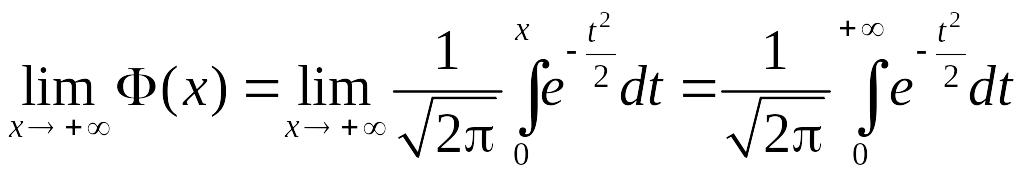Останній невласний інтеграл з нескінченною верхньою межею називається інтегралом Пуассона. Можна показати, що його точне значення 0,5. Отже

.

Прямування до граничного значення відбувається досить швидко. Практично при можна вважати, що дорівнює 0,5.

4.

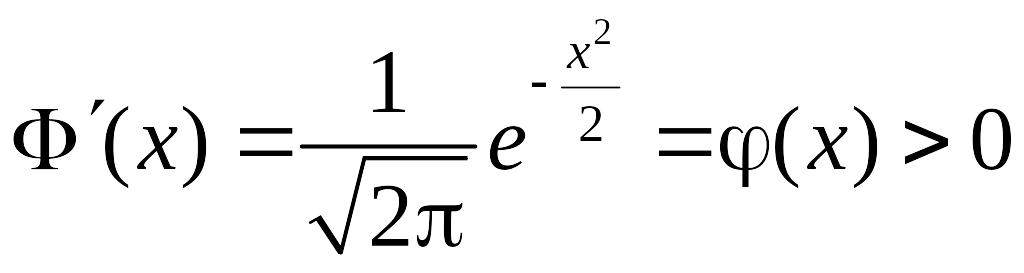, отже функція є зростаючою на всій числовій прямій.

5.

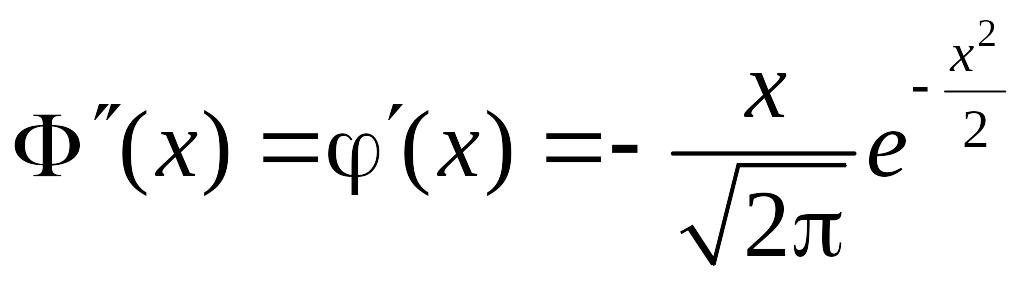, отже при , при , при . Тобто функція є вгнутою при і опуклою при . Точка є точкою перегину даної функції. Схематичний графік функції наведено на рис. 11.

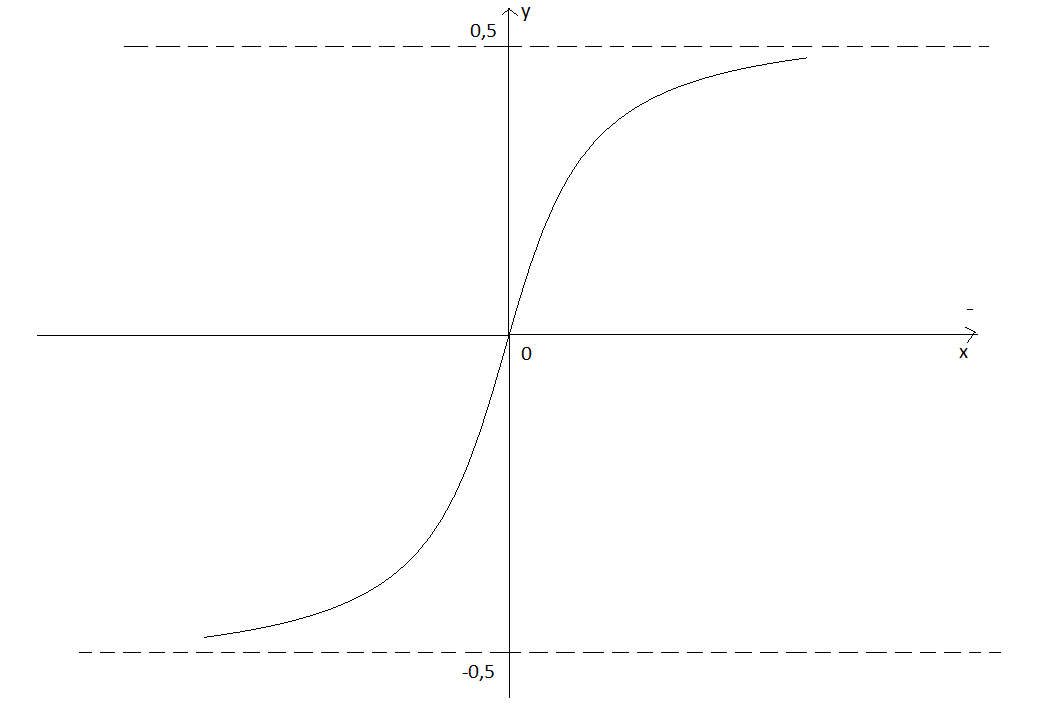
Рис. 11.

Зауважимо, що первісна від функції не виражається в елементарних функціях. Тому для обчислення значень функції ми змушені користуватися наближеними методами обчислення інтегралів. За допомогою таких методів отримано досить детальні таблиці наближених значень функції (див. Додаток, Таблиця 2). Таблиці складено для сітки значень у межах від 0 до 5. При користуємось властивістю непарності функції , а при покладаємо .

Приклади.

1. Досліджують 500 проб руди. Ймовірність промислового вмісту заліза у кожній пробі дорівнює 0,7. Знайти ймовірність того, що кількість проб з промисловим вмістом заліза буде від 300 до 370.

Скористаємось інтегральною теоремою Муавра – Лапласа. Маємо: , , , , .

.

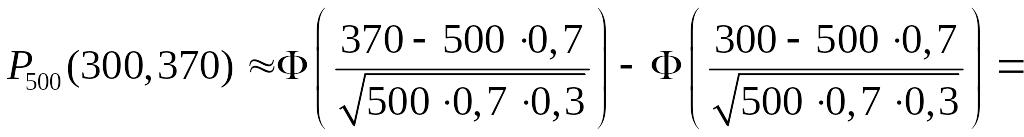
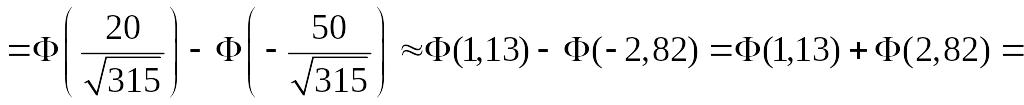
2. Ймовірність присутності студента на лекції дорівнює 0,8. Знайти ймовірність того, що з 100 студентів курсу на лекції буде присутнє не менш, ніж 75.

Маємо: , , , , .

.

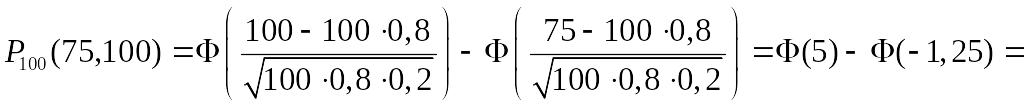
3. Ймовірність появи додатного результату в кожному з випробувань дорівнює 0,9. Скільки треба здійснити випробувань, щоб з ймовірністю 0,98 можна було б чекати, що не менш, ніж 150 випробувань матимуть додатний результат?

Маємо: , , , , . Скористаємось інтегральною теоремою Муавра – Лапласа:

.

Або

.

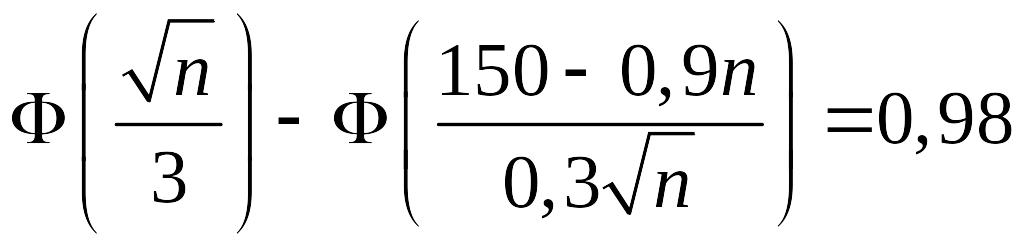Очевидно, що , отже , тому можна покласти . Отже

,

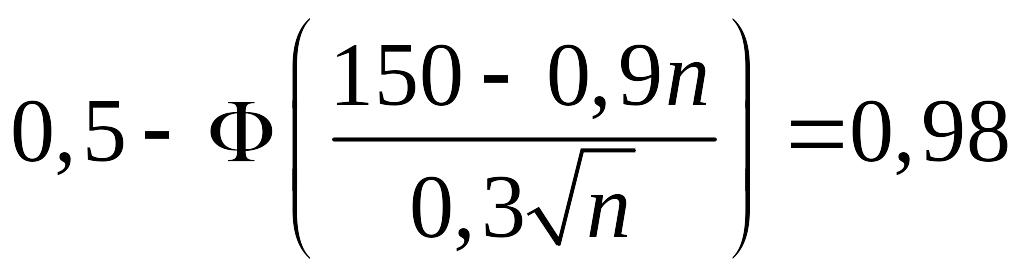звідки

.

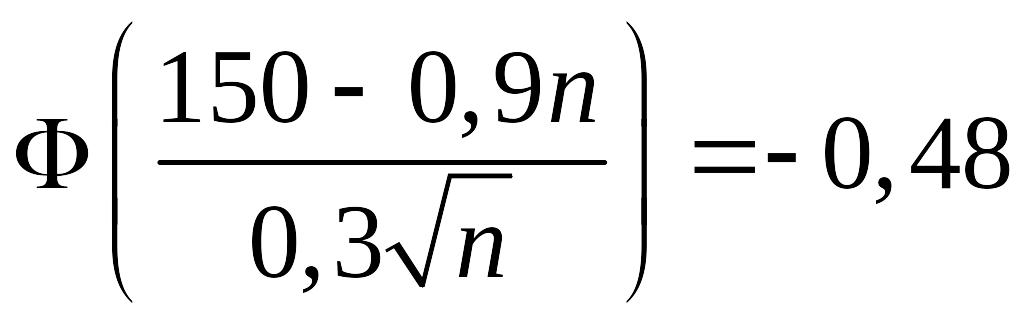За Таблицею 2 (див. Додаток) знайдемо, що значенню 0,48 функції Лапласа відповідає значення аргументу 2,06, тобто . Отже, враховуючи непарність функції Лапласа, отримуємо:

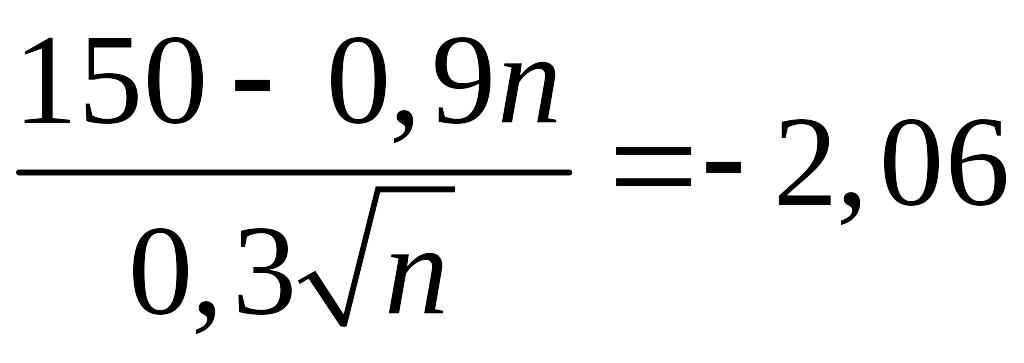, звідки

.

Покладаючи , отримуємо квадратне рівняння:

.

Додатний корінь цього рівняння . Звідси . Таким чином, шукане число випробувань .